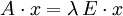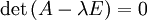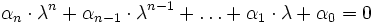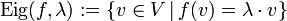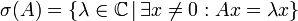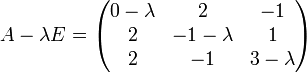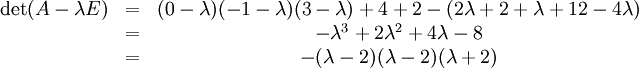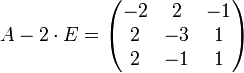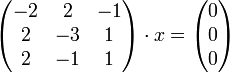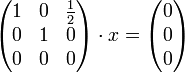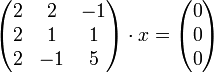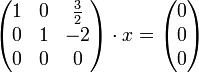Linkseigenvektor

In dieser Scherung der Mona Lisa wurde das Bild so verformt, dass der rote Pfeil (Vektor) entlang der vertikalen Achse seine Richtung nicht geändert hat, während der blaue Pfeil dies tut. Der rote Vektor ist ein Eigenvektor der Scherabbildung, während der blaue Vektor dies aufgrund seiner Richtungsänderung nicht ist. Da der rote Vektor weder gestaucht noch gestreckt wird, ist dessen zugehöriger Eigenwert 1.

Ein Eigenvektor einer Abbildung ist in der linearen Algebra ein vom Nullvektor verschiedener Vektor, dessen Richtung durch die Abbildung nicht verändert wird. Ein Eigenvektor wird also nur gestreckt, und man bezeichnet den Streckungsfaktor als Eigenwert der Abbildung.

Eigenwerte charakterisieren wesentliche Eigenschaften linearer Abbildungen, etwa ob ein entsprechendes lineares Gleichungssystem eindeutig lösbar ist oder nicht. In vielen Anwendungen beschreiben Eigenwerte auch physikalische Eigenschaften eines mathematischen Modells.

Die im Folgenden beschriebene mathematische Problemstellung heißt spezielles Eigenwertproblem und bezieht sich nur auf lineare Abbildungen eines endlichdimensionalen Vektorraums in sich (Endomorphismen), wie sie durch quadratische Matrizen dargestellt werden.

Definition

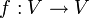Ist V ein Vektorraum über einem Körper K (in Anwendungen meist der Körper $\R$ der reellen Zahlen oder der Körper $\mathbb C$ der komplexen Zahlen) und $f : V \to V$ eine lineare Abbildung von V in sich (Endomorphismus), so bezeichnet man als Eigenvektor einen Vektor 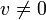$v \ne 0$, der durch f auf ein Vielfaches 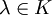$\lambda \in K$ von sich selbst abgebildet wird:

$f(v) = \lambda \, v$.

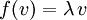Den Faktor λ nennt man dann den zugehörigen Eigenwert.

Anders formuliert: Hat für ein 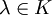$\lambda \in K$ die Gleichung

$f(v) = \lambda \, v$

eine Lösung 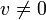$v \ne 0$ (der Nullvektor ist natürlich immer eine Lösung), so heißt λ Eigenwert von f. Jede Lösung 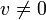$v \ne 0$ heißt Eigenvektor von f zum Eigenwert λ.

Ist der Vektorraum endlichdimensional, so kann jeder Endomorphismus f durch eine quadratische Matrix A beschrieben werden. Die obige Gleichung lässt sich dann als Matrizengleichung schreiben:

$A \cdot x = \lambda \,x$,

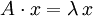wobei x hier einen Spaltenvektor bezeichnet. Man nennt eine Lösung 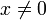$x \ne 0$ und λ in diesem Fall Eigenvektor bzw. Eigenwert der Matrix A.

Diese Gleichung kann man auch in der Form

$A \cdot x = \lambda \,E \cdot x$

schreiben, wobei E die Einheitsmatrix bezeichnet, und äquivalent zu

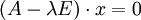$(A - \lambda E) \cdot x = 0$ bzw.

$(\lambda E - A) \cdot x = 0$

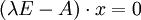
umformen.

Manchmal bezeichnet man einen so definierten Eigenvektor auch als Rechtseigenvektor und definiert dann entsprechend den Begriff des Linkseigenvektors durch die Gleichung

$x^\top \cdot A= \lambda \, x^\top$.

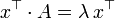Wegen 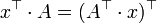$x^\top \cdot A = (A^\top \cdot x)^\top$ sind die Linkseigenvektoren von A gerade die Rechtseigenvektoren der transponierten Matrix $A^\top$.

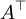Allgemeiner kann man auch quadratische Matrizen A und B betrachten und die Gleichung

$A \cdot x = \lambda \, B \cdot x$.

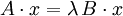Dieses allgemeinere Eigenwertproblem wird hier jedoch nicht betrachtet.

Berechnung der Eigenwerte einer Matrix

Bei kleinen Matrizen können die Eigenwerte symbolisch mit Hilfe des charakteristischen Polynoms berechnet werden. Bei großen Matrizen ist dies oft nicht möglich, sodass hier Verfahren der numerischen Mathematik zum Einsatz kommen.

Symbolische Berechnung

Die Gleichung

$\left(A - \lambda E\right) \cdot x = 0$,

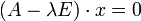die Eigenwerte definiert, stellt ein homogenes lineares Gleichungssystem dar. Da 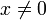$x \neq 0$ vorausgesetzt wird, ist dieses genau dann lösbar wenn gilt:

$\det\left(A - \lambda E\right) = 0$

Expandiert man die Determinante auf der linken Seite, so erhält man ein Polynom n-ten Grades in λ. Dieses wird charakteristisches Polynom (siehe dort zur Herleitung) bezeichnet, und dessen Nullstellen sind die Eigenwerte, also die Lösungen der Gleichung

$\alpha_n\cdot\lambda^n+\alpha_{n-1}\cdot\lambda^{n-1}+\dots+\alpha_1\cdot\lambda+\alpha_0=0$

Da ein Polynom vom Grad n höchstens n Nullstellen besitzt, gibt es höchstens n Eigenwerte. Zerfällt das Polynom vollständig, wie es jedes Polynom über $\mathbb C$ tut, so gibt es genau n Nullstellen, wobei mehrfache Nullstellen mit ihrer Vielfachheit gezählt werden.

Eigenraum zum Eigenwert

Ist λ ein Eigenwert der linearen Abbildung 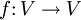$f \colon V \to V$, dann nennt man die Menge aller Eigenvektoren zu diesem Eigenwert vereinigt mit dem Nullvektor den Eigenraum zum Eigenwert λ. Der Eigenraum ist definiert durch:

$\mathrm{Eig} (f, \lambda) := \{v \in V \,|\, f(v) = \lambda \cdot v \}$

Eine Verallgemeinerung des Eigenraums ist der Hauptraum.

Spektrum und Vielfachheiten

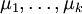Mehrfaches Vorkommen eines bestimmten Eigenwertes fasst man zusammen und erhält so nach Umbenennung die Aufzählung $\lambda_1,\dots, \lambda_k$ der verschiedenen Eigenwerte mit ihren Vielfachheiten $\mu_1,\dots,\mu_k$. Dabei ist 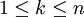$1\leq k \leq n$ und $\sum_{i=1}^k \mu_i=n$.

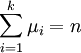Die eben dargestellte Vielfachheit eines Eigenwertes als Nullstelle des charakteristischen Polynoms bezeichnet man als algebraische Vielfachheit.

Die Menge der Eigenwerte wird Spektrum genannt und 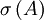$\sigma\left(A\right)$ geschrieben. Es gilt also:

$\sigma(A)=\{\lambda\in\mathbb{C}\,|\,\exists x\neq 0: Ax =\lambda x\}$

Als Spektralradius bezeichnet man den Betrag des betragsmäßig größten Eigenwerts.

Kennt man die Eigenwerte und ihre Vielfachheiten (die algebraische und die später erklärte geometrische), kann man die Jordansche Normalform der Matrix erstellen.

Die geometrische Vielfachheit ist immer kleiner oder gleich der algebraischen Vielfachheit.

Beispiel

Gegeben sei die quadratische Matrix

$A=\begin{pmatrix}0 & 2 & -1 \\ 2 & -1 & 1 \\ 2 & -1 & 3 \end{pmatrix}$.

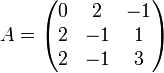Subtraktion der mit λ multiplizierten Einheitsmatrix von A:

$A-\lambda E = \begin{pmatrix} 0 - \lambda & 2 & -1 \\ 2 & -1 - \lambda & 1 \\ 2 & -1 & 3 - \lambda \end{pmatrix}$

Ausrechnen der Determinante dieser Matrix (mit Hilfe der Regel von Sarrus):

$\begin{matrix}\det(A-\lambda E)&=&(0-\lambda)(-1-\lambda)(3-\lambda)+4+2-(2\lambda+2+\lambda +12- 4\lambda) \\ &=&-\lambda^3+2\lambda^2+4\lambda-8 \\ &=&-(\lambda-2)(\lambda-2)(\lambda+2) \end{matrix}$

Die Eigenwerte entsprechen den Nullstellen des Polynoms, d. h. die rechte Seite der obigen Gleichung gleich Null setzen und man erhält:

$\lambda_1=2,\ \lambda_2=-2$

Der Eigenwert 2 hat algebraische Vielfachheit 2, da er doppelte Nullstelle des charakteristischen Polynoms ist.

Numerische Berechnung

Während die Lösung des charakteristischen Polynoms für Matrizen der Dimension 3 schon nicht so einfach ist, wird es für große Matrizen nahezu unmöglich. Hierzu gibt es Verfahren, die sowohl von der numerischen Stabilität her, als auch vom Rechenaufwand wesentlich besser sind. Dazu gehören Methoden für dichtbesetzte kleine bis mittlere Matrizen, wie

• der QR-Algorithmus,
• der QZ-Algorithmus,
• der QS-Algorithmus,

sowie spezielle Methoden für symmetrische Matrizen, als auch Methoden für dünnbesetzte große Matrizen, wie

• die Potenzmethode,
• die Inverse Iteration,
• das Lanczos-Verfahren,
• das Arnoldi-Verfahren,
• das Jacobi-Verfahren und
• das Jacobi-Davidson-Verfahren.

Des Weiteren gibt es noch Methoden zur Abschätzung, wie

• die Gerschgorin-Kreise

die immer eine grobe Abschätzung, unter gewissen Bedingungen sogar genaue Bestimmung zulässt.

• Die Folded Spectrum Method liefert mit jedem Durchlauf einen Eigenvektor, welcher jedoch auch aus der Mitte des Spektrums stammen kann.

Berechnung der Eigenvektoren

Für einen Eigenwert λ lassen sich die Eigenvektoren aus der Gleichung

$(A-\lambda E) \cdot x = 0$

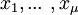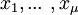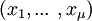bestimmen. Die Eigenvektoren spannen einen Raum auf, dessen Dimension als geometrische Vielfachheit des Eigenwertes bezeichnet wird. Für einen Eigenwert λ der geometrischen Vielfachheit μ lassen sich also Eigenvektoren $x_1,...\ ,x_\mu$ finden, so dass die Menge aller Eigenvektoren zu λ gleich der Menge der Linearkombinationen von $x_1,...\ ,x_\mu$ ist. $(x_1,...\ ,x_\mu)$ heißt dann Basis aus Eigenvektoren zum Eigenwert λ.

Die geometrische Vielfachheit eines Eigenwertes kann man also auch als die maximale Anzahl linear unabhängiger Eigenvektoren zu diesem Eigenwert definieren.

Die geometrische Vielfachheit ist immer kleiner oder gleich der algebraischen Vielfachheit.

Beispiel

Gegeben ist wie im oberen Beispiel die quadratische Matrix A:

$A=\begin{pmatrix}0 & 2 & -1 \\ 2 & -1 & 1 \\ 2 & -1 & 3 \end{pmatrix}$

Die Eigenwerte 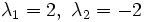$\lambda_1=2 ,\ \lambda_2=-2$ wurden oben schon berechnet. Zunächst werden hier die Eigenvektoren (und der durch die Eigenvektoren aufgespannte Eigenraum) zum Eigenwert λ₁ = 2 berechnet.

$A - 2 \cdot E = \begin{pmatrix} -2 & 2 & -1 \\ 2 & -3& 1 \\ 2 & -1 & 1 \end{pmatrix}$

man muss also das folgende lineare Gleichungssystem lösen:

$\begin{pmatrix} -2 & 2 & -1 \\ 2 & -3& 1 \\ 2 & -1 & 1 \end{pmatrix} \cdot x= \begin{pmatrix}0\\ 0\\ 0 \end{pmatrix}$

Bringt man die Matrix auf obere Dreiecksform erhält man:

$\begin{pmatrix} 1 & 0 & \frac{1}{2} \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{pmatrix} \cdot x= \begin{pmatrix}0\\ 0\\ 0 \end{pmatrix}$

Die Lösung (und damit die gesuchten Eigenvektoren) ist der Vektor 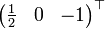$\begin{pmatrix}\frac{1}{2} & 0 & -1 \end{pmatrix}^\top$ und alle seine Vielfachen (nicht jedoch das Nullfache des Vektors, da Nullvektoren niemals Eigenvektoren sind).

Obwohl dieser Eigenwert eine algebraische Vielfachheit von 2 hat, existiert nur ein linear unabhängiger Eigenvektor (der Eigenraum zu den einzelnen Eigenwerten hat Dimension 1); also hat dieser Eigenwert eine geometrische Vielfachheit von 1. Das hat eine wichtige Konsequenz: Die Matrix ist nicht diagonalisierbar. Man kann nun versuchen, die Matrix stattdessen in die Jordansche Normalform zu überführen. Dazu muss ein weiterer Eigenvektor zu diesem Eigenwert „erzwungen“ werden. Diese Eigenvektoren nennt man generalisierte Eigenvektoren oder Hauptvektoren. Schlägt auch das fehl, so kann die Matrix auch nicht in die Jordansche Normalform überführt werden.

Für den Eigenwert λ₂ = − 2 geht man genauso vor:

$\begin{pmatrix} 2 & 2 & -1 \\ 2 & 1 & 1 \\ 2 & -1 & 5 \end{pmatrix} \cdot x= \begin{pmatrix}0\\ 0\\ 0 \end{pmatrix}$

wieder bringt man die Matrix auf Dreiecksform

$\begin{pmatrix} 1 & 0 & \frac{3}{2} \\ 0 & 1 & -2 \\ 0 & 0 & 0 \end{pmatrix} \cdot x= \begin{pmatrix}0\\ 0\\ 0 \end{pmatrix}$

Hier ist die Lösung der Vektor 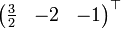$\begin{pmatrix}\frac{3}{2} & -2 & -1 \end{pmatrix}^\top$ wieder mit allen seinen Vielfachen.

Eigenschaften

• Ist λ ein Eigenwert der invertierbaren Matrix A zu Eigenvektor x, so ist $\frac{1}{\lambda}$ Eigenwert der inversen Matrix von A zum Eigenvektor x.
• Sind λ_i die Eigenwerte der Matrix 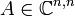$A\in\mathbb{C}^{n,n}$, so gilt

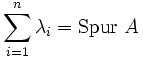$\sum_{i=1}^n \lambda_i = \operatorname{Spur} \; A$ und $\prod_{i=1}^n \lambda_i = \operatorname{det} \; A$,

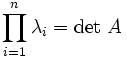wobei bei mehrfachen Eigenwerten die Vielfachheit zu beachten ist.

• Zu einer symmetrischen reellen Matrix A lässt sich immer eine Basis aus orthogonalen Eigenvektoren angeben. ^[1] Insbesondere sind Eigenvektoren zu verschiedenen Eigenwerten dann zueinander orthogonal.
• Eigenvektoren zum Eigenwert 1 sind Fixpunkte in der Abbildungsgeometrie.
• Anhand der Eigenwerte kann man die Definitheit einer Matrix bestimmen. So sind die Eigenwerte von reellen symmetrischen Matrizen reell. Ist die Matrix echt positiv definit so sind die Eigenwerte reell und echt größer Null.
• Die aus den Vorzeichen der Eigenwerte errechnete Signatur einer symmetrischen Matrix verhält sich gemäß dem Trägheitssatz von Sylvester.
• Jede quadratische Matrix A über dem Körper $\mathbb{C}$ der komplexen Zahlen ist ähnlich zu einer oberen Dreiecksmatrix B. Die Eigenwerte von A sind genau die Diagonaleinträge der Matrix B.
• Das Spektrum einer Matrix A ist gleich dem Spektrum der transponierten Matrix, also: 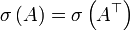$\sigma\left(A\right) = \sigma\left(A^\top\right)$. Analog gilt: $\sigma\left(A^*\right) = \sigma\left(\overline{A}\right)$.

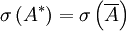Verallgemeinerung auf unendlich dimensionale Vektorräume

Hauptartikel: Spektraltheorie

In der Funktionalanalysis betrachtet man lineare Abbildungen zwischen linearen Funktionenräumen. Zu diesen Abbildungen kann man ebenfalls ein Spektrum und Eigenvektoren finden. Oftmals spricht man in diesem Zusammenhang von Eigenfunktionen anstatt von Eigenvektoren. Diese Spektraltheorie ist die Verallgemeinerung der Eigenwerttheorie.

Praktische Beispiele

Durch Lösung eines Eigenwertproblems berechnet man

• Eigenfrequenzen, Eigenformen und gegebenenfalls auch Dämpfungscharakteristik eines schwingfähigen Systems,
• Knicklast eines Knickstabs (siehe Balkentheorie),
• Beulversagen eines leeren Rohres unter Außendruck,
• Die Hauptkomponenten einer Punktmenge, z. B. zur Kompression von Bildern oder Bestimmung von Faktoren in der Psychologie. (Hauptkomponentenanalyse).
• Hauptspannungen in der Festigkeitslehre: Umrechnung der Spannungen in ein Koordinatensystem, in dem es keine Schubspannungen gibt,
• Hauptträgheitsachsen eines unsymmetrischen Querschnitts, um einen Balken (Träger oder ähnliches) in diesen beiden Richtungen unabhängig voneinander zu berechnen,
• vielfältige andere technische Problemstellungen, die mit der jeweils spezifisch definierten Stabilität eines Systems zu tun haben.

Eigenwerte spielen in der Quantenmechanik eine besondere Rolle. Physikalische Größen wie z. B. der Drehimpuls werden hier durch Operatoren repräsentiert. Messbar sind nur die Eigenwerte der Operatoren. Hat z. B. der Hamiltonoperator, der die Energie eines quantenmechanischen Systems repräsentiert, ein diskretes Spektrum, so kann die Energie nur diskrete Werte annehmen, was z. B. für die Energieniveaus in einem Atom typisch ist. Auch die Unmöglichkeit der gleichzeitigen präzisen Messung gewisser Größen (z. B. Ort und Impuls), wie von der Heisenbergschen Unschärferelation ausgedrückt, ist in diesem Fall letztlich darauf zurückzuführen, dass für die jeweiligen Operatoren kein gemeinsames System von Eigenvektoren gefunden werden kann.

Weblinks

• Online-Tool zum Berechnen von Eigenwerten etc. auch großer Matrizen
• Z. Bai, J. Demmel, J. Dongarra, A. Ruhe, and H. van der Vorst, editors. Templates for the Solution of Algebraic Eigenvalue Problems: A Practical Guide. SIAM, Philadelphia, 2000.
• Eigenvectors and Eigenvalues. Video der Vorlesung "Lineare Algebra" von Gilbert Strang, MIT, 2000.

Einzelnachweise

1. ↑ Uni Tübingen Symmetrische Abbildungen und Matrizen Theorem 10.75 abgerufen am 19. Februar 2007

Literatur

Gerd Fischer: Lineare Algebra, Vieweg-Verlag, ISBN 3-528-03217-0