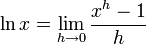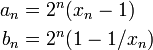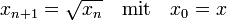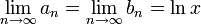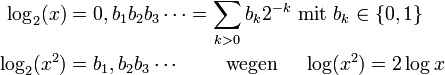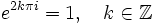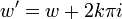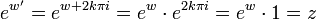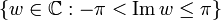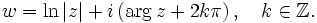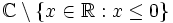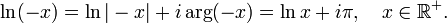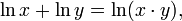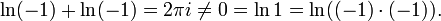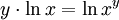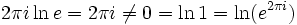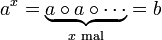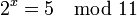- Logaritmus
-
 Logarithmische Skaleneinteilung eines Rechenschiebers (Detail)
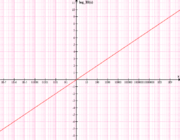
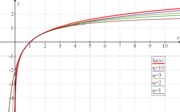
Logarithmische Skaleneinteilung eines Rechenschiebers (Detail)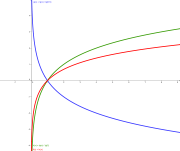 Graph des Logarithmus zur Basis 2 (grün), e (rot) bzw. 1/2 (blau)
Graph des Logarithmus zur Basis 2 (grün), e (rot) bzw. 1/2 (blau)Der Logarithmus (Mehrzahl: Logarithmen, von gr. λόγος lógos „Verständnis, Lehre“, αριθμός arithmós „Zahl“) gehört zu den elementaren mathematischen Funktionen.
Die Verwendung des Logarithmus lässt sich bis in die indische Antike zurückverfolgen. Mit dem aufstrebenden Bankwesen und dem Fortschritt der Astronomie im Europa des 17. Jahrhunderts erlangte der Logarithmus immer mehr an Bedeutung. Seine Funktionswerte wurden in Tabellenwerken, den Logarithmentafeln, erfasst, um sie nachschlagen zu können und nicht immer neu berechnen zu müssen. Diese Tabellen wurden schließlich durch Rechenschieber und Taschenrechner verdrängt.
Die Stärke eines Sinneseindrucks in Abhängigkeit von einer physikalischen Größe wie Helligkeit oder Lautstärke, zeigt den Verlauf einer Logarithmusfunktion. Gleiches gilt für die wahrgenommene Tonhöhe in Abhängigkeit von der Frequenz eines Tones.
Logarithmen erlangten ihre historische Bedeutung durch den Zusammenhang
- log(xy) = logx + logy
der es erlaubt, eine Multiplikation durch eine Addition auszudrücken.
Formal sind Logarithmen alle Lösungen der Gleichung
- a = bx
zu vorgegebenen Größen a und b. Je nach dem, über welchem Zahlenbereich und für welche Größen diese Gleichung betrachtet wird, hat sie keine, mehrere oder genau eine Lösung. Ist die Lösung eindeutig, dann wird sie als der Logarithmus von a zur Basis b bezeichnet und man schreibt
- x = logba.
Am bekanntesten und am weitesten verbreitet ist der Logarithmus über den reellen Zahlen, der im Folgenden vornehmlich dargestellt wird.
Geschichte
Indische Mathematiker im 2. Jahrhundert v. Chr. haben als Erste Logarithmen erwähnt. Schon in der Antike nutzten sie Logarithmen für ihre Berechnungen zur Basis der Zahl Zwei. Im 8. Jahrhundert beschrieb der indische Mathematiker Virasena Logarithmen zur Basis Drei und Vier. Ab dem 13. Jahrhundert wurden von arabischen Mathematikern ganze logarithmische Tabellenwerke erstellt.
Der deutsche Mathematiker Michael Stifel formulierte im Jahr 1544 folgende Beziehungen: qmqn = qm + n und
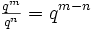 . Diese Erkenntnis ist der Schlüssel zu den Logarithmen. Stifel ließ nur ganzzahlige Exponenten zu. Napiers Idee war dagegen, einen stetigen Wertebereich für die Exponenten zuzulassen.
. Diese Erkenntnis ist der Schlüssel zu den Logarithmen. Stifel ließ nur ganzzahlige Exponenten zu. Napiers Idee war dagegen, einen stetigen Wertebereich für die Exponenten zuzulassen.Im 17. Jahrhundert entwickelte der Schweizer Uhrmacher Jost Bürgi (1552–1632) ein neues System zur Berechnung von Logarithmen, welches er 1620 nach langer Arbeit veröffentlichte. Aber schon vorher, im Jahre 1614, veröffentlichte der schottische Denker John Napier (1550–1617) ein Buch über Logarithmen, das ihn als „Erfinder der Logarithmen“ berühmt machte. Ihre Arbeiten und Erkenntnisse über Logarithmen entwickelten Jost Bürgi und John Napier jedoch unabhängig voneinander.
Das griechische Wort „Logarithmus“ bedeutet auf Deutsch „Verhältniszahl“ und stammt von Napier. Erstmals veröffentlicht wurden Logarithmen von diesem unter dem Titel Mirifici logarithmorum canonis descriptio, was mit Beschreibung des wunderbaren Kanons der Logarithmen übersetzt werden kann.
Nachdem sich der Oxforder Professor Henry Briggs (1561–1630) intensiv mit dieser Schrift beschäftigte, nahm er mit deren Autor Kontakt auf und schlug vor, für die Logarithmen die Basis 10 zu verwenden. Diese verbreiteten sich schnell und wurden besonders in der Astronomie geschätzt, was auch Pierre-Simon Laplace feststellte:
- „Durch die Arbeitserleichterung infolge der Verwendung von Logarithmen wird das Leben der Astronomen verdoppelt.“
Heute wird die Eulersche Zahl e als Basis der Exponentendefinition des natürlichen Logarithmus verwendet, welche im Jahre 1728 von Leonhard Euler (1707–1783) bestimmt und erstmals 1742 veröffentlicht wurde.
Mit den Logarithmen war die mathematische Grundlage für die Weiterentwicklung des mechanischen Rechenschiebers gelegt; denn die Funktionsweise des Rechenschiebers basiert auf dem Prinzip der Addition und Subtraktion von Logarithmen.
Logarithmus in Anwendung und Natur
Anwendungen des Logarithmus finden sich vielfach in der Wissenschaft, wenn der Wertebereich viele Größenordnungen umfasst. Daten werden entweder direkt mit einer logarithmischen Skala dargestellt, oder die Einheiten selbst sind logarithmisch, wie zum Beispiel beim pH-Wert oder dem Dezibel.
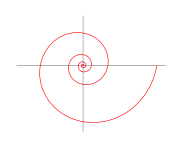
 Das Gehäuse eines Nautilus zeigt eine logarithmische Spirale
Das Gehäuse eines Nautilus zeigt eine logarithmische Spirale- In der belebten Natur
- finden sich zahlreiche Beispiele logarithmischer Spiralen, so z. B. das Wachstum von Schneckenhäusern oder die Anordnung der Kerne auf der Sonnenblume.
- pH-Wert
- Der Säurewert von Lösungen. Anmerkung: In der Chemie kann man logarithmische Skalen i. A. am vorangestellten p erkennen, z. B. beim pKs- oder pKb-Wert.
- Dezibel (dB)
- Messung von Lautstärke, elektronischer Dämpfung, etc.
- Die Empfindlichkeit der Sinnesorgane
- folgt dem logarithmischen Weber-Fechner-Gesetz der Psychophysik, wonach eine Vervielfachung der Reizstärke nur eine lineare Zunahme des wahrgenommenen Reizes bewirkt.
- Sternhelligkeiten
- werden in astronomischen Größenklassen angegeben, die ein logarithmisches Maß der tatsächlichen Strahlungsstärke darstellt.
- Rechenschieber
- Bevor elektronische Rechenmaschinen zur Verfügung standen, nutzte man die Logarithmengesetze aus, um Multiplikationen zu Additionen und Divisionen zu Subtraktionen zu vereinfachen. Die Berechnung der Quadratwurzel vereinfacht sich auf der Ebene des Logarithmus zu einer Division durch Zwei. Weil der Logarithmus selbst nicht so leicht zu berechnen ist, waren Rechenschieber mit ihren logarithmischen Skaleneinteilungen und Logarithmentafeln weit verbreitete Hilfsmittel.
- Lösung von typischen Aufgabenstellungen, die bei Wachstums- oder Zerfallsprozessen
- auftreten, da diese durch seine Umkehrfunktion, die Exponentialfunktion, modelliert werden. Siehe Exponentieller Vorgang, Absorption.
- Anzahl der Ziffern einer Zahl
- Berechnung der Anzahl der Ziffern, die zur Darstellung einer natürlichen Zahl in einem Stellenwertsystem benötigt werden. Um eine natürliche Zahl n zur Basis b darzustellen, werden
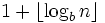 Stellen benötigt. Die Klammern bedeuten dabei Abrunden auf die nächste ganze Zahl, die kleiner oder gleich ist.
Stellen benötigt. Die Klammern bedeuten dabei Abrunden auf die nächste ganze Zahl, die kleiner oder gleich ist. - Zum Beispiel ist
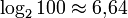 . Die obige Formel liefert den Wert 7. Man braucht also 7 Ziffern, um 100 im Dualsystem darzustellen, nämlich 100 = 11001002. Stellt man hingegen 100 im Hexadezimalsystem dar, dann benötigt man dazu zwei Stellen, denn
. Die obige Formel liefert den Wert 7. Man braucht also 7 Ziffern, um 100 im Dualsystem darzustellen, nämlich 100 = 11001002. Stellt man hingegen 100 im Hexadezimalsystem dar, dann benötigt man dazu zwei Stellen, denn 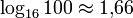 . Es ist 100 = 6416.
. Es ist 100 = 6416.
- Benfordsches Gesetz
- Die Verteilung der Ziffern von Zahlen in empirischen Datensätzen, zum Beispiel ihrer ersten Ziffern, folgt einer logarithmischen Verteilung, dem Benford'schen Gesetz.
- Informationseinheit
- Messung der Informationsmenge; die Informationstheorie sagt, dass, wenn etwas mit Wahrscheinlichkeit p auftritt, das Wissen über das tatsächliche Auftreten davon eine Informationsmenge von
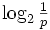 bit ergibt. Zum Beispiel erhält man beim Ergebnis „Kopf“ eines fairen Münzwurfs (p = 0,5) die Informationsmenge log22 = 1 bit, und es genügt ein Bit, um diese Information zu codieren.
bit ergibt. Zum Beispiel erhält man beim Ergebnis „Kopf“ eines fairen Münzwurfs (p = 0,5) die Informationsmenge log22 = 1 bit, und es genügt ein Bit, um diese Information zu codieren.
- Kryptographie
- Der diskrete Logarithmus ist in endlichen Körpern und darauf definierten elliptischen Kurven erheblich aufwändiger zu berechnen als seine Umkehrfunktion, die diskrete Exponentialfunktion. Letztere kann daher als sogenannte Einwegfunktion in der Kryptografie zur Verschlüsselung angewandt werden.
- Logarithmische Zeitskalen
- finden sich in der Geschichte der Technologie ebenso wie in der geologischen Zeitskala.
- Zur graphischen Darstellung von Funktionen
- werden spezielle mathematische Papiere verwendet, wie z. B. einfachlogarithmisches Papier oder doppeltlogarithmisches Papier.
Bezeichnungen
Man schreibt:
und sagt: „x ist der Logarithmus von a zur Basis b“ oder auch „x ist der Logarithmus zur Basis b aus a“. a heißt Numerus oder veraltet auch Logarithmand.[1] Das Ergebnis des Logarithmierens gibt also an, mit welchem Exponenten x man die Basis b potenzieren muss, um den Logarithmanden (Numerus) a zu erhalten. Das setzt voraus, dass das Potenzieren mit beliebigen reellen Exponenten schon erklärt ist (was auf verschiedene Weise geht, aber ohne vorherige Kenntnis des Logarithmus nicht ganz einfach ist).
Das Formelzeichen für den Logarithmus ist log. Die Basis wird als Index angehängt. Seltener findet man auch davon abweichende Schreibweisen, wie zum Beispiel bloga, oder die Basis wird nicht mitnotiert, wenn sie aus dem Zusammenhang ersichtlich ist und keine Verwechslungsgefahr besteht.
Für die Vorkommastellen des Logarithmus wird teilweise der Begriff Kennzahl verwendet, und seine Nachkommastellen werden Mantisse genannt.
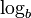
- Logarithmus zur Basis b
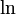
- logarithmus naturalis bzw. natürlicher Logarithmus, der Logarithmus zur Basis e, der eulerschen Zahl 2,7182818284590452…
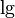
- Dekadischer Logarithmus, auch bezeichnet als Zehnerlogarithmus oder Briggsscher Logarithmus ist der Logarithmus zur Basis 10. Er ist nützlich wegen des Zehnersystems und wird von vielen Taschenrechnern verwendet.
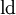
- logarithmus dualis, Logarithmus zur Basis 2, auch als Zweierlogarithmus oder dyadischer oder binärer Logarithmus bezeichnet (manchmal auch mit der Abkürzung
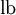 ); wird in der Informatik aufgrund des Binärsystems verwendet.
); wird in der Informatik aufgrund des Binärsystems verwendet. 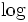
- Das Symbol log ohne eine angegebene Basis wird verwendet, wenn diese aus dem Zusammenhang ersichtlich oder aufgrund einer Konvention festgelegt ist. In technischen Anwendungen (so z. B. auf den meisten Taschenrechnern) steht log meist für den dekadischen Logarithmus, in der Informatik für den dyadischen Logarithmus. Mathematiker und Physiker verwenden log meist für den natürlichen Logarithmus. Gelegentlich wird log auch verwendet, wenn die verwendete Basis keine Rolle spielt.
Ein ähnliches Formelsymbol ist
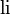 für den Integrallogarithmus. Bei dieser Funktion handelt es sich nicht um eine Logarithmusfunktion.
für den Integrallogarithmus. Bei dieser Funktion handelt es sich nicht um eine Logarithmusfunktion.Definition
Der Logarithmus über den positiven reellen Zahlen kann auf verschiedene Art und Weisen eingeführt werden. Je nach Hintergrund und Intention wird man den einen oder anderen Zugang wählen.
Die einzelnen Definitionen sind untereinander äquivalent und erfolgen mit besonderem Fokus auf den natürlichen Logarithmus, der aus Sicht des Mathematikers auf natürliche Art auftritt, wie bei dem Zugang über die Funktionalgleichung oder über die Stammfunktion von 1 / t erkennbar wird.
Als Umkehrfunktion der Exponentialfunktion
Der Logarithmus zur Basis b ist die Umkehrfunktion der allgemeinen Exponentialfunktion zur Basis b:
Die Funktionen bx und logbx sind also Umkehrfunktionen voneinander, d. h. Logarithmieren macht Exponenzieren rückgängig und umgekehrt:
Der natürliche Logarithmus ergibt sich mit der Basis b = e, wobei
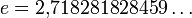 die eulersche Zahl ist.
die eulersche Zahl ist.Als Lösung einer Funktionalgleichung
Die Logarithmusfunktionen sind die nicht-trivialen, stetigen Lösungen L der Funktionalgleichung
Diese Lösungen erweisen sich sogar als differenzierbar. Den natürlichen Logarithmus erhält man dann zusammen mit der Zusatzbedingung
- L'(1) = 1.
Die Zusatzbedingung ist einer der Gründe dafür, den so erhaltenen Logarithmus als natürlich zu bezeichnen. Wollte man den Logarithmus zu einer anderen Basis b über die Zusatzbedingung erhalten, dann müsste man
fordern und würde wieder den natürlichen Logarithmus benötigen.
Die triviale Lösung obiger Funktionalgleichung ist die Nullfunktion L(x) = 0, welche nicht als Logarithmusfunktion angesehen wird.
Als Stammfunktion von 1/t
Die Funktion
mit x > 0 ist gerade der natürliche Logarithmus: Es ist L = ln. Zum Logarithmus mit der Basis b gelangt man durch Division der Funktion L durch die Konstante L(b) = lnb.
Als Potenzreihe
Der natürliche Logarithmus kann als Potenzreihe gemäß
eingeführt werden. Diese Reihe hat den Konvergenzradius 1. Durch analytische Fortsetzung oder durch Anwendung der Funktionalgleichung
erhält man den natürlichen Logarithmus auf den positiven reellen Zahlen.
Als Isomorphismus
Die reellwertigen Logarithmen sind genau die stetigen Isomorphismen
Diese Definition legt die Funktion L bis auf eine multiplikative Konstante eindeutig fest.
Der algebraische Zugang betont ebenso wie der Zugang über die Funktionalgleichung die historische Bedeutung des Logarithmus als Rechenhilfe: Er ermöglicht es, eine Multiplikation in eine Addition "umzuwandeln".
Anmerkung
Diese Definitionen können auch herangezogen werden, um Logarithmen auf anderen mathematischen Strukturen zu erhalten, wie z. B. auf den komplexen Zahlen. Das setzt voraus, dass in der betreffenden Struktur die zur Definition verwendeten Konzepte existieren.
Um etwa den diskreten Logarithmus auf einer Gruppe zu definieren, können Konzepte wie Differentiation/Integration sowie Multiplikation/Division nicht herangezogen werden, weil sie dort gar nicht existieren. (In einer Gruppe gibt es eine Verknüpfung und nicht zwei, die zudem noch durch ein Distributivgesetz miteinander verknüpft sind).
Rechenregeln und grundlegende Eigenschaften
Logarithmengesetze
Im Folgenden wird stets vorausgesetzt, dass die Variablen x,y,xi,r,a,b von Null verschieden sind; im Falle des reellen Logarithmus werden die Zahlen sogar als positiv vorausgesetzt. Die Basis a des Logarithmus darf ferner nicht 1 sein.
Produkte
Für das Rechnen mit Logarithmen von Produkten steht die hilfreiche Rechenregel
zur Verfügung; oder allgemeiner:
bzw.
Der Logarithmus eines Produkts ist die Summe der Logarithmen der Faktoren.
Quotienten
Die Quotienten leiten sich direkt aus den Logarithmen von Produkten ab. Hier sei nur der einfache Fall
angegeben. Der Logarithmus eines Quotienten ist der Logarithmus des Zählers x minus den Logarithmus des Nenners y.
Summen und Differenzen
Aus der Formel für Produkte kann eine Formel für Logarithmen von Summen (und Differenzen) wie x + y hergeleitet werden, indem x ausgeklammert wird:
Damit ergeben sich die Regeln
Potenzen
Für Potenzen mit reellem Exponent r gilt die Regel
Der Logarithmus einer Potenz ist also das Produkt aus dem Exponenten mit dem Logarithmus der Basis.
Daraus lässt sich für r = − 1
ermitteln.
Der Logarithmus eines Stammbruchs 1 / x ist der negative Logarithmus des Nenners x.
Diese Rechenregeln lassen sich von den Potenzgesetzen ableiten.
Wurzeln
Da Wurzeln nichts anderes als Potenzen mit gebrochenem Exponenten sind, ergibt sich nach der oben angegebenen Potenzregel des Logarithmus die Rechenregel
Basisumrechnung
Um Logarithmen zur Basis b mithilfe von Logarithmen einer beliebigen Basis a zu berechnen, verwendet man den Zusammenhang
denn es gelten mit
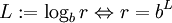 die Umformungen
die UmformungenDie meisten Tabellenwerke oder Taschenrechner stellen Logarithmen nur zur Basis 10 und natürliche Logarithmen zur Verfügung. Mit obiger Formel lassen sich daraus Logarithmen zu einer beliebigen Basis berechnen.
- Beispiel:
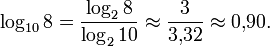
Alternative mit Hilfe des natürlichen Logarithmus:
Null und die negativen Zahlen
In den reellen Zahlen ist der Logarithmus für Null und negative Zahlen nicht definiert.
Begründungen
- x = loga0 müsste dann 0 = ax bedeuten. Ist a ungleich Null, ist dies jedoch für kein reelles x lösbar.
- (als Beispiel die negative Zahl −1) x = loga( − 1) müsste dann − 1 = ax bedeuten. Dies ist ebenfalls für keine reelle Zahl x möglich, wenn a größer Null ist.
In der Funktionentheorie, in der Funktionen von komplexen Zahlen betrachtet werden, kann man den Logarithmus auch für negative Zahlen definieren (siehe Komplexer Logarithmus), allerdings gelten dann einige der Rechenregeln nicht mehr. Auch in diesem Zusammenhang ist 0 keine isolierte Singularität sondern ein Verzweigungspunkt.
Ableitung und Integral
Die natürliche Logarithmusfunktion ist die Umkehrfunktion der Exponentialfunktion. Daher erhält man die Ableitung des natürlichen Logarithmus einfach durch Anwendung der Umkehrregel (siehe Beispiel dort).
Es ergibt sich
Für allgemeine Logarithmen gilt:
Das unbestimmte Integral des natürlichen Logarithmus erhält man mit partieller Integration:
Ist bei einem bestimmten Integral des natürlichen Logarithmus eine der Grenzen Null, so kann die Regel von L'Hospital angewendet werden.
- Beispiel:
![\int_0^1{\ln x\,\mathrm dx} = [x\ln{x}-x]_0^1 = -1,](/pictures/dewiki/100/d1246200921e41c41789b42898fd4684.png)
da
Kurvendiskussion
- Definitionsmenge:
![D = ]0,\infty[](/pictures/dewiki/51/35c9b604c6c96a5cad88ae543cc648c3.png)
- Wertemenge: alle reellen Zahlen
- Nullstellen bzw. Schnittpunkte mit den Koordinatenachsen: {1} bzw. (1|0)
- Gebräuchliche Limites/Verhalten im Unendlichen:
- Erste Ableitung:
- Extrempunkte: keine
- Wendepunkte: keine
- Monotonie: streng monoton steigend/wachsend (wenn b > 1) bzw. fallend (sonst)
Natürlicher Logarithmus und andere spezielle Logarithmen
Der Logarithmus zur Basis e (der eulerschen Zahl) wird auch als natürlicher Logarithmus bezeichnet und mit „ln“ oder oft auch „log“ (ohne Subskript) abgekürzt:
- Wenn y = ex, dann ist x = logey = lny.
Die Zahl e ist z. B. dadurch ausgezeichnet (und könnte auch so definiert werden), dass die Exponentialfunktion ex sich bei Ableitung nach x wieder selbst reproduziert, als Formel:
Der Begriff natürlicher Logarithmus wurde gewählt, weil sowohl die Exponentialfunktion als auch der Logarithmus zur Basis e in vielen Zusammenhängen (Integralrechnung, Differentialrechnung, Komplexe Zahlen, Trigonometrie) auf natürliche Weise ohne Vorfaktoren auftreten. Insbesondere lässt sich der natürliche Logarithmus sehr einfach integrieren und differenzieren.
Der natürliche Logarithmus von x, also F(x) = lnx ist eine Stammfunktion der Potenzfunktion
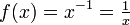 .
.Berechnung des Logarithmus
Potenzreihe
des natürlichen Logarithmus um den Entwicklungspunkt 1 konvergiert nicht sonderlich schnell.
Zur Berechnung verwendet man besser folgende Reihendarstellung, die auf der Potenzreihenentwicklung des Areatangens Hyperbolicus beruht:
mit der Restgliedabschätzung
Die Reihe zeigt für x und 1 / x ähnliches Konvergenzverhalten und konvergiert umso besser, je näher x bei 1 liegt. Um dies zu erreichen, verwendet man
Durch Wahl einer geeigneten ganzen Zahl m kann man immer erreichen, dass gilt
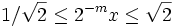 und erhöht damit die Konvergenzgeschwindigkeit der Reihe, die man jetzt für 2 − mx berechnet. Allerdings muss man zusätzlich noch eine Näherung für
und erhöht damit die Konvergenzgeschwindigkeit der Reihe, die man jetzt für 2 − mx berechnet. Allerdings muss man zusätzlich noch eine Näherung für 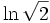 berechnen, was über die gleiche Reihe erfolgt.
berechnen, was über die gleiche Reihe erfolgt.Wenn man aus obiger Formel die Restgliedabschätzung entfernt, erhält man:
Grenzwerte nach Hurwitz
Für den natürlichen Logarithmus gelten die Grenzwerte
sowie gleichbedeutend damit
die man leicht mit der Regel von L’Hospital bestätigt.
Hierauf basieren die von Adolf Hurwitz für den natürlichen Logarithmus angegebenen Grenzwerte der Folgen an bzw. bn, die über
wobei
definiert sind. Wegen
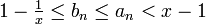 und weil an monoton fallend und bn monoton wachsend ist, folgt die Konvergenz dieser beiden Folgen. Aufgrund von an = bnxn und xn→1 ergibt sich die Gleichheit der beiden Grenzwerte:
und weil an monoton fallend und bn monoton wachsend ist, folgt die Konvergenz dieser beiden Folgen. Aufgrund von an = bnxn und xn→1 ergibt sich die Gleichheit der beiden Grenzwerte:Für eine praktische Berechnung von ln x sind diese Grenzwerte wegen der auftretenden Auslöschung jedoch nicht gut geeignet.
Berechnung einzelner Binärziffern
Eine weitere Möglichkeit zur Berechnung des Logarithmus besteht darin, nacheinander die Ziffern der Binärdarstellung des Logarithmus zur Basis 2 zu bestimmen. Dieses Verfahren ist besonders einfach auf Rechenwerken zu implementieren, da es aufwändige Divisionen vermeidet und auch leicht in Festkomma-Arithmetik umsetzbar ist.
Zunächst werden die Vorkommastellen des Zweierlogarithmus (immer im Dualsystem) durch Abzählen der Vorkommastellen der Zahl x bestimmt, und die Zahl x durch Schieben auf Werte zwischen 1 und 2 normiert.
Der Logarithmus von x hat danach die Darstellung
Quadrieren von x schiebt den Logarithmus also um eine Binärstelle nach links, wodurch die Vorkommastelle möglicherweise Eins wird. Dies ist dann der Fall, wenn x2 ≥ 2 ist. In diesem Falle wird x durch Division durch 2 wieder normiert, was keinen Einfluss auf die verbleibenden Stellen hat. Damit ergibt sich die folgende Skizze des Verfahrens:
INPUT 1 ≤ x < 2 OUTPUT Nachkommastellen bi der Binärdarstellung von log2(x) i ← 0 LOOP i ← i + 1 x ← x2 IF x ≥ 2 THEN x ← x / 2 bi ← 1 ELSE bi ← 0 END IF END LOOPAnalogrechner
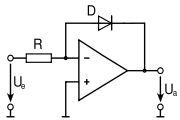
Zur Berechnung des Logarithmus mithilfe eines Analogrechners – also etwa der Erzeugung einer Ausgangsspannung, die den Logarithmus des Nennwerts der Eingangsspannung annimmt – kann man sich den exponentiellen Verlauf der Strom-Spannungs-Kennlinie einer Diode zunutze machen. Die nebenstehende Skizze zeigt den prinzipiellen Aufbau eines Logarithmierers mit Verwendung einer Halbleiterdiode D. Denkbar wäre auch die Verwendung einer Röhre mit adäquater Beschaltung.
Komplexer Logarithmus
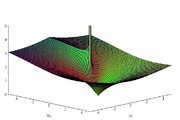
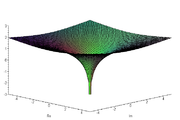
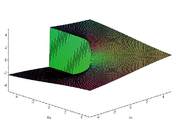
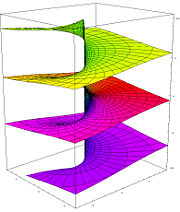 Riemannsche Fläche der komplexen Logarithmus-Funktion, die Blätter entstehen aufgrund der Mehrdeutigkeit
Riemannsche Fläche der komplexen Logarithmus-Funktion, die Blätter entstehen aufgrund der MehrdeutigkeitAnalog zur reellen Definition heißt jede komplexe Zahl w, welche die Gleichung
- ew = z
erfüllt, ein natürlicher Logarithmus von z. Dies ist im Unterschied zum reellen Logarithmus jedoch nicht eindeutig, da
gilt, siehe dazu auch Eulersche Identität. Hat man also einen Logarithmus w von z gefunden, so ist damit auch
ein Logarithmus von z, da gilt:
Um Eindeutigkeit zu erreichen, schränkt man w auf einen Streifen in der komplexen Zahlenebene ein. Man kann z. B. den Streifen
verwenden. Eine komplexe Zahl aus diesem Streifen heißt Hauptwert des Logarithmus und man schreibt w = lnz. Stellt man z in Polarkoordinaten dar, so erhält man eine einfache Darstellung des k-ten Zweigs der Logarithmusfunktion:
Für k = 0 hat man dann den Hauptzweig des Logarithmus:
- lnz = ln | z | + iargz
ln ist nicht stetig auf
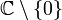 . Entfernt man jedoch die negative reelle Achse, so ist ln auf dem Gebiet
. Entfernt man jedoch die negative reelle Achse, so ist ln auf dem Gebietstetig und sogar holomorph. Allgemeiner gilt dies für alle einfach zusammenhängenden, offenen Teilmengen von
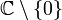 .
.Mit dem Hauptzweig des komplexen Logarithmus kann man den Logarithmus von negativen, reellen Zahlen bestimmen:
Man muss jedoch beachten, dass im Komplexen die Rechenregeln für Logarithmen nicht immer gelten, sondern nur noch modulo 2πi. Es gilt dann beispielsweise nicht notwendig
wegen
Und auch die Gleichung
ist nicht notwendig erfüllt, was durch das Gegenbeispiel
verdeutlicht wird.
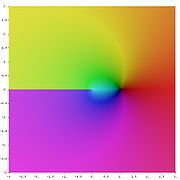
Grafische Darstellung des komplexen Logarithmus Diskrete Logarithmen
→ Hauptartikel: Diskreter Logarithmus
Diskrete Logarithmen sind Lösungen von Gleichungen der Form
über einer endlichen zyklischen Gruppe
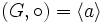 . Der diskrete Logarithmus x von b zur Basis a ist modulo der Gruppenordnung von G eindeutig bestimmt und existiert – da a ein Erzeuger der Gruppe ist – für alle Elemente der Gruppe.
. Der diskrete Logarithmus x von b zur Basis a ist modulo der Gruppenordnung von G eindeutig bestimmt und existiert – da a ein Erzeuger der Gruppe ist – für alle Elemente der Gruppe.Diskrete Logarithmen sind im Sinne der Komplexitätstheorie für viele Gruppen aufwändig zu berechnen und finden Anwendung in der Kryptographie, etwa in auf elliptischen Kurven basierenden Kryptosystemen.
Beispiel:
hat als Lösung den Wert 4, denn es gilt 24 = 16, und 16 lässt den Rest 5 bei Division mit Rest durch 11. Die Lösung ist eindeutig modulo 10, also modulo der Gruppenordnung von
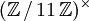 . Dementsprechend ist mit x auch x±10 eine Lösung der Kongruenz.
. Dementsprechend ist mit x auch x±10 eine Lösung der Kongruenz.Literatur
- Wolfgang Walter: Analysis I. Grundwissen Mathematik Band 3. Springer-Verlag, 1985, ISBN 3-540-12780-1 und ISBN 0-387-12780-1.
- Klaus Jänich: Funktionentheorie. Eine Einführung. Springer-Verlag, ISBN 3-540-20392-3.
Siehe auch
- Exponentialfunktion
- Potenzfunktion
- Ableitung
- Dekadischer Logarithmus
- Logarithmus von Ordinalzahlen
- Logarithmische Ableitung
- Logarithmische Darstellung
Weblinks
- Beispiele zur Logarithmusrechnung mit Maple
- Logarithmen
- Logarithmen und Logarithmusgesetze (Onlinekurs, Übungen, Applets und Links)
Einzelnachweise
- ↑ Wissenschaftliche Zeitschrift der Humboldt-Universität zu Berlin. 38, 1989, S. 5
Wikimedia Foundation.


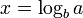
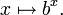
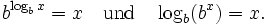
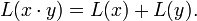
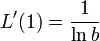
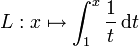
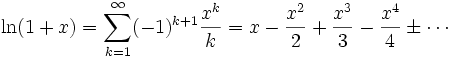
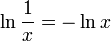
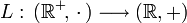
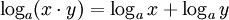
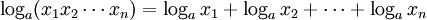
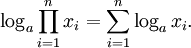
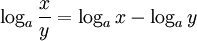
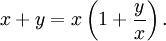
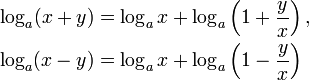
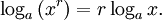
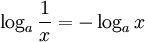
![\log_a \sqrt[n]{x}
= \log_a \left(x^{\frac 1n}\right)
= \frac 1n\log_a x.](/pictures/dewiki/55/7b6ee1cf714ba8820a155e9c703dabb1.png)
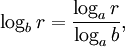
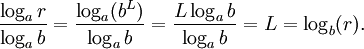
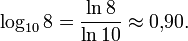
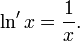
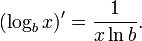
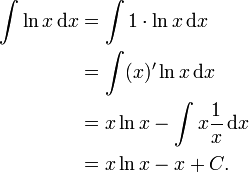
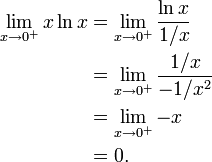
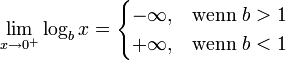
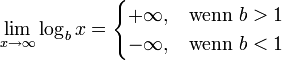
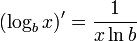
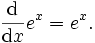
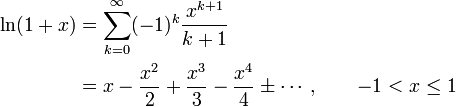
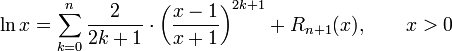
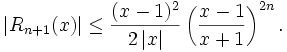
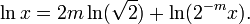
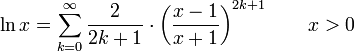
![\ln x = \lim_{n \to \infty} n \left(\sqrt[n]x -1 \right)
= \lim_{n \to \infty} n \left(1-\frac{1}{\sqrt[n]{x}}\right)](/pictures/dewiki/53/5a3f4cb02dddb72eb0a21c42be224df1.png)