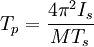Lunisolare Präzession

Präzession eines rotierenden Kreisels

Die Präzession ist allgemein die Richtungsänderung der Achse eines rotierenden Körpers, wenn äußere Kräfte ein Drehmoment auf ihn ausüben. Speziell in der Astronomie ist damit die Richtungsänderung der Erdachse gemeint, die eine Folge der Massenanziehung des Mondes und der Sonne in Verbindung mit der Abweichung der Erdfigur von der Kugelform ist.

Grundlagen

Präzession bei Störung

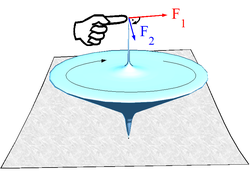
Die Trägheit der rotierenden Kreiselmasse bewirkt bei „Störungen“ durch Krafteinwirkung F1 an der Kreiselachse eine Ausweichbewegung, als wirke am Angriffspunkt der Störkraft eine um 90° in Rotationsrichtung „weitergedrehte“ Kraft F2 (tangential zur Drehbewegung). Vorsicht: Betrachtungen hier und im Folgenden nur für "schnell drehende" Kreisel richtig; im Allgemeinen muss mit den Eulerschen Gleichungen gerechnet werden (aufwendiger).

Demonstration der Kreiselgesetze

Die Präzession ist neben der Stabilität der freien Kreiselachse das zweite der – technisch vielfach nutzbaren – grundlegenden Kreiselgesetze, sie lässt sich bei jedem Spielzeugkreisel beobachten, kann aber bei anspruchsvollerer Konstruktion auch in ihrer Richtungsumkehr zwischen "hängendem" und "stehendem" Kreisel demonstriert werden.

Steht die Drehachse des idealen Kreisels genau senkrecht, also parallel zur Lotrichtung, so wirkt kein Drehmoment auf ihn ein, da die Feldlinien der Schwerkraft in Richtung dieser Drehachse ist. Deshalb bleibt die Achse senkrecht, es findet keine Präzession statt.

Setzt man einen Kreisel schräg auf, würde er infolge der Schwerkraft umkippen, wenn er nicht rotierte. Dieses „Kippmoment“ (analog F1) bewirkt bei einem rotierenden Kreisel, dass seine Drehachse aufgrund der Ausweichbewegung (durch F2) eine Bewegung ausführt, die Präzession.

Ist die Drehachse des Kreisels insbesondere parallel zur Erdoberfläche und ist der Kreisel auf der Drehachse, jedoch nicht im Schwerpunkt gestützt, so präzediert die gesamte Anordnung um den Stützpunkt des Kreisels.

Deutlich zu spüren ist die Ausweichbewegung, wenn man ein ausgebautes, schnell rotierendes Rad eines Fahrrades an den Enden der Radachse in den Händen hält und versucht, das Rad nach rechts oder links zu neigen. Man spürt eine deutliche Kraft, die versucht, die Achse des Rades nach vorne oder hinten zu drehen. Auch beim Gyrotwister, einem kürzlich sehr populären kugelförmigen Hand- und Unterarmmuskulaturtrainer, kann man diesen Effekt deutlich spüren.

Das physikalische Prinzip, welches für die oben beschriebenen Effekte verantwortlich ist, ist die Drehimpulserhaltung.

Technische Anwendungen der Präzession sind etwa der Kreiselkompass, der Wendezeiger, das Zweirad (vgl. Gyroskopischer Effekt bei Zweirädern) oder das Gyroskop als Beschleunigungssensor.

Präzessionsperiode und Präzessionsfrequenz

Die Präzessionsperiode wird bestimmt durch:

$T_p = \frac{4\pi^2I_s}{MT_s}$

Hierbei ist I_s das Trägheitsmoment, T_s die Rotationsperiode und M das Drehmoment. Es handelt sich hierbei um eine Näherungsformel, die gilt, wenn T_s << T_p ist.

Die Präzessionsfrequenz ist der Rotationsfrequenz (Drehzahl) umgekehrt proportional: Je schneller der Körper rotiert, desto weniger schnell taumelt er. Die resultierende Winkeländerung pro Zeit wird bei der Rotation der Erde als Präzessionskonstante bezeichnet.

Präzession der Erdachse

Präzessionsbewegung der Erde mit (stark überzeichneter) Nutation

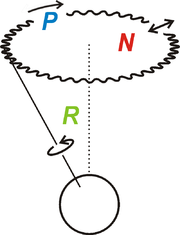
Die Erde hat keine exakte Kugelform, sondern durch die Abplattung des Erdellipsoids von 1:298,25 einen zusätzlichen „Äquatorwulst“ (engl. equatorial bulge) von 21 km. Dadurch bewirken die Gezeitenkräfte von Mond und Sonne ein Drehmoment, welches die Erdachse aufzurichten versucht und zur Präzession der Erdachse führt (auch als Lunisolare Präzession bezeichnet, in der Zeichnung mit P markiert). Für einen vollen Kegelumlauf benötigt die Erdachse um die 25.700–25.800 Jahre. Dieser Zeitraum wird Zyklus der Präzession (auch Platonisches Jahr) genannt und durch die Präzessionskonstante beschrieben.

Auch die Ebene der Mondbahn, die gegenüber der Ekliptik um rund 5° geneigt ist, weist eine Präzessionsbewegung mit einer Periodenlänge von 18,6 Jahren auf; d.h. ihr Normalenvektor beschreibt einen Kegelumlauf mit dieser Umlaufdauer um den Normalenvektor der Ekliptik. Die dadurch verursachte Änderung des Drehmoments hat ebenfalls eine Auswirkung auf die Richtungsänderung der Erdachse: Dem kegelförmigen Präzessionsumlauf überlagert sich eine periodische Abweichung mit einer Amplitude von 9,2" und einer Periode von 18,6 Jahren. Diese nickende Bewegung der Erdachse heißt Nutation. In der Zeichnung ist sie mit N bezeichnet. Daneben gibt es noch weitere Nutationsanteile mit kürzeren Perioden und Amplituden unter 1". (Der hier verwendete astronomische Begriff der Nutation ist nicht identisch mit dem in der Mechanik verwendeten Begriff der Nutation in der Kreiseltheorie.)

Auswirkungen

Die Präzession der Erdachse führt dazu, dass das tropische Jahr, das sich nach dem Winkel der Erdachse zur Sonne richtet, etwa 20 Minuten kürzer ist als das siderische Jahr (ein Umlauf um die Sonne). Dadurch verändert sich die Schnittlinie Äquator-Ekliptik (der sog. Frühlingspunkt), welcher als eine Art „Nullmeridian“ auf der Himmelssphäre dient. Infolgedessen ändern sich auch die Koordinaten der Fixsterne am Himmel langsam – um etwa 0,014°, also 50,4" pro Jahr.
Dieser Effekt ist schon seit über 2000 Jahren bekannt. Der griechische Astronom Hipparchos verglich etwa um 150 v. Chr. die Sternörter seines neu gemessenen Kataloges mit den Daten aus mehrere hundert Jahre alten Aufzeichnungen und stellte Unterschiede fest. Die Babylonier dürften die Präzession aber schon 170 Jahre früher entdeckt haben.

Gegenwärtig zeigt die Erdachse recht genau in Richtung des Polarsterns, um den sich scheinbar alle Fixsterne drehen. Als Folge der Präzession wird in fernerer Zukunft der Himmelspol nicht mehr beim Polarstern liegen, sondern in verschiedenen Sternbildern auf einem Kreis von 23,5° Radius (Schiefe der Ekliptik) um den Ekliptikpol. In 12.000 Jahren wird er sich bei der Wega im Sternbild Leier befinden, dem zweithellsten nördlichen Stern.

Im Rahmen der Milanković-Zyklen gibt es einen Einfluss der Präzession auf die Eiszeiten, über dessen Ausmaß aber noch Unklarheit herrscht.

Siehe auch

• Nutation (Physik) – die nicht durch äußere Kräfte verursachte Bewegung der Achse eines Kreisels
• Nutation (Astronomie) – die Nutation von Himmelskörpern, insbesondere der Erde
• Künstlicher Horizont – wo die Präzession als Störeffekt auftritt
• Präzession des Perizentrums bzw. Perihels – ein Effekt mit anderer physikalischer Ursache

Weblinks

• Beschreibung mit animierter Grafik
• Präzession der Erdachse in der Astronomie-Bibliothek auf Astronomie.de
• Präzession eines seitlich von seinem Schwerpunkt aufgehängten rotierenden Rades