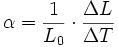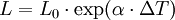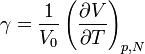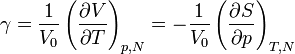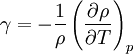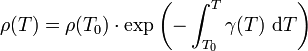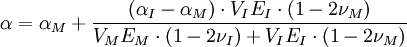Längenausdehnungkoeffizient

Der Ausdehnungskoeffizient oder Wärmeausdehnungskoeffizient ist ein Kennwert, der das Verhalten eines Stoffes bezüglich Veränderungen seiner Abmessungen bei Temperaturveränderungen beschreibt - deswegen oft auch thermischer Ausdehnungskoeffizient genannt. Der hierfür verantwortliche Effekt ist die Wärmeausdehnung. Da die Wärmeausdehnung bei vielen Stoffen nicht gleichmäßig über alle Temperaturbereiche erfolgt, ist auch der Wärmeausdehnungskoeffizient selbst temperaturabhängig und wird deshalb für eine Bezugstemperatur oder einen Temperaturbereich angegeben.

Es wird zwischen dem thermischen Längenausdehnungskoeffizienten α (auch linearer Wärmeausdehnungskoeffizient oder Wärmedehnung) und dem thermischen Raumausdehnungskoeffizienten γ (auch räumlicher Ausdehnungskoeffizient oder Volumenausdehnungskoeffizient oder kubischer Ausdehnungskoeffizient) unterschieden:

Linearer Wärmeausdehnungskoeffizient

Der lineare Ausdehnungskoeffizient gibt an, um welche Längendifferenz im Verhältnis zur gesamten Länge L₀, sich ein fester Körper bei einer Temperaturänderung von einem Kelvin verändert. Er ist eine stoffspezifische Größe, die für einen homogen Festkörper definiert ist durch:

$\alpha = \frac{1}{L_0} \cdot \frac{\Delta L}{ \Delta T} \,$

Die Längenänderung eines Stabes bei gleichmäßiger Erwärmung oder Abkühlung um die Temperaturdifferenz ΔT kann berechnet werden, indem der lineare Ausdehnungskoeffizient α des Stabmaterials mit der Stablänge L₀ und der Temperaturdifferenz ΔT multipliziert wird:

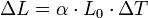$\Delta L = \alpha \cdot L_0 \cdot \Delta T$ bzw. $L = L_0 (1 + \alpha \cdot \Delta T) \,$

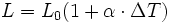
Bei großen Temperaturdifferenzen ist genauer:

$L = L_0 \cdot \exp (\alpha \cdot \Delta T) \,$

Bei anisotropen Festkörpern kann auch die Messrichtung einen Einfluss haben, was es in Bezug auf die Aussagekraft der Stoffwerte zu beachten gilt.

Volumenspezifischer Ausdehnungskoeffizient

Der volumenspezifische Ausdehnungskoeffizient gibt an, um welchen Betrag im Verhältnis zum gesamten Volumen sich das Volumen eines Körpers bei einer Temperaturänderung von einem Kelvin vergrößert oder verkleinert. Anders ausgedrückt: Der volumenspezifische Ausdehnungskoeffizient beschreibt die relative Änderung des Volumens V mit der Temperatur T. Er ist definiert durch (die den partiellen Ableitungen als Index nachgestellte Größen sind konstant zu halten: Druck p, Teilchenzahl N):

$\gamma=\frac{1}{V_0}\left(\frac{\part V}{\part T} \right)_{p,N} \,$

Für isotrope (kubische) Festkörper gilt: $\gamma \approx 3 \cdot \alpha \,$.

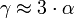Mit einer Maxwell-Relation ist es möglich, den thermischen Ausdehnungskoeffizient mit der Entropie S in Verbindung zu bringen:

$\gamma=\frac{1}{V_0}\left(\frac{\part V}{\part T} \right)_{p,N} = -\frac{1}{V_0}\left(\frac{\part S}{\part p} \right)_{T,N} \,$

Der volumenspezifische Ausdehnungskoeffizient ergibt sich, da die Masse 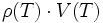$\rho(T) \cdot V(T)$ temperaturunabhängig ist, aus der Dichte ρ(T) in Abhängigkeit von der Temperatur:

$\gamma=-\frac{1}{\rho}\left(\frac{\part \rho}{\part T} \right)_p \,$

Ist der Ausdehnungskoeffizient als Funktion der Temperatur bekannt, so ergibt sich die Dichte aus:

$\rho(T)=\rho(T_0) \cdot \exp \left( - \int_{T_0}^{T} \gamma (T) \ \mathrm dT \right) \,$

Hierbei ist T₀ eine beliebige Temperatur, z.B. T₀ = 298,15 K = 25 °C, bei der die Dichte ρ(T₀) bekannt ist.

Grüneisen hat gezeigt, dass der Quotient α / c_p zwischen dem thermischen Ausdehnungskoeffizienten 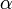$\alpha\$ und der spezifischen Wärmekapazität c_p unabhängig von der Temperatur ist.

Im Allgemeinen ist der Wärmeausdehnungskoeffizient eine positive Größe. Wegen des Massenerhaltungssatzes geht daher bei den meisten Stoffen eine Temperaturerhöhung mit einer Verringerung der Dichte einher. Manche Stoffe wie beispielsweise Wasser zwischen 0 und 4 °C zeigen jedoch in einem bestimmten Temperaturbereich ein ungewöhnliches Verhalten, das man als Dichteanomalie bezeichnet. Außerdem gibt es Materialien wie zum Beispiel einige Arten von Glaskeramik, deren Wärmeausdehnungskoeffizient nahezu null ist.

Der Wärmeausdehnungskoeffizient wird auf empirischen Wege durch Messungen ermittelt und gilt nur für den Stoff und für den Temperaturbereich, an beziehungsweise in dem die Messung erfolgte.

Beispiele

Gase verhalten sich meistens annähernd als ideales Gas, das sich proportional zur Temperatur in Kelvin ausdehnt und demzufolge bei 0 °C (273,15 K) einen Ausdehnungskoeffizienten von 1/273,15 K⁻¹hat.

Längenausdehnungskoeffizient α einiger Feststoffe Bezeichnung α in 10−6 K−1 bei 20 °C Acryl 90,0 Aluminium, gewalzt 23,2 Aluminium, rein 23,0 Antimon 10,5 Aramidfaser (HM-Faser in Längsrichtung) −4,1 Bakelit (mit Holzmehl) 50,0 Bakelit (mit Asbest) 30,0 Beryllium 12,3 Beton 6 bis 14 Bismut 14,0 Blei 29,3 Bronze 17,5 Cadmium 41,0 Chrom 6,2 Diamant 1,3 Eis, 0 °C 51,0 Eisen 12,2 Germanium 6,0 Gummi (leicht vulkanisiert) 220,0 Gummi (mit Ruß) 160,0 Glas (Fensterglas) 7,6 Glas (Geräteglas) 4,5 Glas (BK7) 7.1 Glas (Borsilikatglas, Duran, Pyrex) 3,25 Glas (Quarzglas) 0,5 Glaskeramik (Zerodur) < 0,1 Gold 14,2 Granit 3,0 Graphit 2,0 Grauguss 9,0 Holz, Eiche 8,0 Invar 1,7-2,0 Iridium 6,5 Kochsalz 40,0 Kohlenstofffaser (HM 35 in Längsrichtung) -0,5 Konstantan 15,2 Kovar um 5 Kupfer 16,5 Magnesium 26,0 Mangan 23,0 Mauerwerk 5,0 Messing 18,4 Molybdän 5,2 Neusilber 18,0 Nickel 13,0 Platin 9,0 Polyamid (Nylon) 120,0 Polyethylen 100,0 bis 250,0 [1] Polystyrol 70,0 Polyester 80,0 Polyester mit 70% Glasfaser in GF-Richtung 12,0 Polymethylmethacrylat (PMMA) 85,0 Polyvinylchlorid, biegsam (PVC) 240,0 Polyvinylchlorid, steif (PVC) 50,0 Polytetrafluorethylen, (PTFE) 200,0 Porzellan 3,0 Silber 19,5 Silizium 2,0 Stahl 13,0 Stahl, rostfrei 10,0…16,0 Titan 10,8 Wolfram 4,5 Zink 26,3 Zinn 26,7

Raumausdehnungskoeffizient γ einiger Flüssigkeiten Bezeichnung γ in 10−3 K−1 bei 20 °C Ethanol 1,10 Aceton (Propanon) 1,43 Benzin 1,06 Benzol 1,23 Chloroform (Trichlormethan) 1,28 Essigsäure 1,07 Ether 1,62 Ethylacetat 1,38 Glyzerin (Propantriol) 0,49 Methanol 1,10 Mineralöl (Hydrauliköl) 0,70 Paraffin 0,76 Petroleum 0,96 Quecksilber 0,182 Terpentinöl 1,00 Tetrachlormethan 1,22 Toluol 1,12 Wasser 0,21

Zweiphasige Werkstoffe

Für zweiphasige Werkstoffe, die aus einer Matrixphase und einer eingelagerten oder durchdringenden Phase bestehen, ergibt sich der lineare thermische Ausdehnungskoeffizient aus folgender Formel:

$\alpha=\alpha_M+\frac{(\alpha_I-\alpha_M)\cdot V_I E_I \cdot (1-2 \nu_M)}{V_M E_M \cdot(1-2 \nu_I) + V_I E_I \cdot(1-2\nu_M)} \,$

Hierbei bezeichnen α_M bzw α_I die Wärmeausdehnungskoeffizienten, V_M bzw V_I die Volumenanteile, E_M bzw E_I die Elastizitätsmoduln und ν_M bzw ν_I die Querkontraktionszahlen der Matrixphase (Index M) bzw. der eingelagerten Phase (Index I).

Quellen

1. ↑ Vorlesungsskript TU München

Literatur

• G. Ondracek: Werkstoffkunde. Leitfaden für Studium und Praxis. 2. Aufl., Expert-Verlag, 1986, ISBN 3-88508-966-1.
• Böhler (Hrsg.): Edelstahl-Handbuch. Eigenverlag, Kapfenberg (Österreich).

Siehe auch

• Wärmeausdehnung
• Temperaturkoeffizient