- Maschenstromanalyse
-
Als Maschenstromverfahren bezeichnet man ein in der Elektrotechnik verwendetes Verfahren zur Netzwerkanalyse. Mit dieser Methode lassen sich die Zweigströme bestimmen. Denn jedes elektrische Netzwerk aus linearen Bauelementen kann auf diese Weise durch ein lineares Gleichungssystem beschrieben und berechnet werden.
Vorgehen
- Baum wählen
- Das Netzwerk vereinfachen, d. h. Parallelschaltungen vereinen.
- Ideale Stromquellen als Sehne wählen, das Gleichungssystem vereinfacht sich dadurch.
- Nicht-ideale Stromquellen in äquivalente Spannungsquellen umwandeln.
- Baum markieren.
- Maschen festlegen
- Jede Masche (M) läuft über nur eine Sehne, ansonsten schließt sich diese über die Äste des Baumes
- Bei jeder Masche muss der Umlaufsinn festgelegt werden. Vom Umlaufsinn hängt die Wahl der Vorzeichen ab.
- Matrix aufstellen
![[R] \cdot [I_M] = [U_{qM}]](/pictures/dewiki/49/1f09c1e1d1b0f42160c391de0f465b02.png) [1], mit komplexen Größen
[1], mit komplexen Größen ![[\underline Z] \cdot [\underline {I}_M] = [ \underline {U}_{qM}]](/pictures/dewiki/97/ae234dc94547705488b179843b0f7b1d.png)
In die Hauptdiagonale der Widerstandsmatrix trägt man die Summe aller Widerstände, über die sich die jeweilige Masche schließt, ein. Die Dimension der Matrix ist die Anzahl der Maschen abzüglich der idealen Stromquellen im Netzwerk.
In die anderen Felder trägt man die Summen der Widerstände ein, mit denen sich die Maschen überschneiden. Bei gegensätzlichem Umlaufsinn bekommt die Summe ein negatives Vorzeichen.
In die Quellspannungsmatrix trägt man die Summe aller Spannungsquellen ein, die in der jeweiligen Masche liegen. Das Vorzeichen ist positiv, wenn der Umlaufsinn ungleich dem Spannungspfeil ist.
Ideale Stromquellen (Iq) müssen anders behandelt werden. Die zugehörige Masche (MIq) wird nicht in die Matrix aufgenommen, sowohl Zeile als auch Spalte entfallen. Die Lösung des Maschenstromes ist bereits gegeben, IMi = Iq. Der Überlappung mit den anderen Maschen wird Rechnung getragen, indem der Spannungsabfall auf den gemeinsamen Widerständen durch die ideale Stromquelle in die Quellspannungsmatrix mit einfließt.
- Gleichungssystem lösen
Die aufgestellte Gleichung ist ein lineares Gleichungssystem. Durch das Gaußsches Eliminationsverfahren oder die Cramer’sche Regel lässt sich dieses durch systematisches Vorgehen lösen.
- Zweigströme berechnen
Nach dem Überlagerungsprinzip berechnet sich der Strom in einem Zweig (vorzeichenrichtig) aus der Summe der Maschenströme, die diesen durchlaufen.
Beispiel:
- I1 = IM1 + IM2 − IM3
Einzelnachweise
Siehe auch
Wikimedia Foundation.





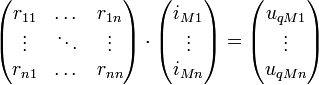
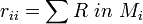
![r_{ij} = r_{ji} = \sum [R\ in\ M_i\ und\ M_j \cdot Umlaufsinn(M_i,M_j)]](/pictures/dewiki/99/cd067fb59f73d919d0e565a4334d5067.png)
![u_{qMi} = \sum [U_q\ in\ M_i \cdot (-1) \cdot Pfeil(U_q,M_i)]](/pictures/dewiki/52/4e6971088a67e03b34c2e8c8845bd778.png)
![u_{qMi} = \sum [U_q\ in\ M_i \cdot (-1) \cdot Pfeil(U_q,M_i)] - I_q \cdot \sum [R\ in\ M_i\ und\ M_{Iq} \cdot Umlaufsinn(M_i,M_{Iq})]](/pictures/dewiki/99/c194ca0ebb1228ca286380cb4e6a5d00.png)