Maschinenepsilon

Die Maschinengenauigkeit ist ein Maß für den Rundungsfehler, der bei der Rechnung mit Gleitkommazahlen auftritt.

Beschreibung

Aufgrund der endlichen Mantisse in der Gleitkommadarstellung lassen sich Zahlen auf einem Computer nicht beliebig genau darstellen. Es muss gerundet werden. Statt x verwendet der Computer die Zahl rd(x) für die weitere Rechnung.

Für den dabei auftretenden relativen Rundungsfehler gilt:

$\left| \frac{x-rd(x)}{x}\right| \le \varepsilon = \frac{1}{2} \beta^{1-t}$

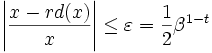
Dabei wird ε als Maschinengenauigkeit bezeichnet. β ist die Basis der Gleitkommadarstellung und t die Mantissenlänge. Die Maschinengenauigkeit gibt also den maximalen relativen Rundungsfehler an.

Bemerkungen

Die angegebene Abschätzung für den Rundungsfehler gilt nur für normalisierte Gleitkommazahlen. Nähert man sich der Zahl Null, so kann der relative Rundungsfehler auch größer werden und steigt bis auf 100% (für rd(x) = 0).

Es sind auch andere Bezeichnungen für die Maschinengenauigkeit gebräuchlich. Insbesondere sind dies Rundungseinheit (unit roundoff) und manchmal auch Maschinenepsilon (bzw. macheps). Wobei der Begriff Maschinenepsilon auch für den maximalen relativen Abstand zweier Gleitkommazahlen verwendet wird.

Beispiel

Als Beispiel soll ein Zahlensystem zur Basis 2 mit der Mantissenlänge 3 genommen werden. Das Bild zeigt die entsprechenden Gleitkommazahlen im Bereich 1 bis 8.

Die Zahl 4,2 wird in diesem System auf 4 gerundet werden. Der absolute Rundungsfehler ist dann:

| x − rd(x) | = | 4,2 − rd(4,2) | = | 4,2 − 4 | = 0,2

Der relative Rundungsfehler ergibt sich aus:

$\left| \frac{x-rd(x)}{x}\right| = \frac{0,2}{4,2} =\frac{1}{21} \approx 0,05$

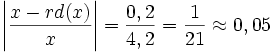
Dieser ist natürlich kleiner als die Maschinengenauigkeit für dieses Beispiel 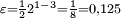$\scriptstyle \varepsilon=\frac{1}{2}2^{1-3}=\frac{1}{8}=0,125$. Die Maschinengenauigkeit ist also im Allgemeinen eine sogenannte worst case Abschätzung.

Bedeutung

Das Ergebnis einer Rechnung ist wesentlich von der Maschinengenauigkeit abhängig. Zunächst können die Eingangsdaten nicht beliebig genau dargestellt werden. Daraus resultiert ein Fehler im Ergebnis. Dieser Fehler wird über die Kondition des Problems beschrieben. Multipliziert man die Kondition mit der Maschinengenauigkeit erhält man eine Abschätzung dieses Fehlers. Die zweite Fehlerquelle entsteht aus der Ungenauigkeit des verwendeten Algorithmus. Diese Fehlerverstärkung wird als Stabilität bezeichnet. Auch hierfür lässt sich manchmal die entsprechende Stabilitätskonstante angeben. Ein schlecht konditioniertes Problem oder ein mäßig stabiler Algorithmus erfordern also eine hohe Maschinengenauigkeit oder eine geeignete Problemumformulierung beziehungsweise die Verwendung eines stabileren Algorithmus.

Maschinengenauigkeit in der Praxis

Heutige Computer arbeiten meist nach IEEE 754. Die Maschinengenauigkeit für die dabei verwendeten Datentypen ist 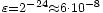$\scriptstyle \varepsilon=2^{-24}\approx 6\cdot10^{-8}$ für einfache Genauigkeit (single precision) und 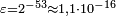$\scriptstyle \varepsilon=2^{-53}\approx 1,1\cdot10^{-16}$ für doppelte Genauigkeit (double precision).

Literatur

• A. Kielbasinski und H. Schwetlick: Numerische lineare Algebra Deutscher Verlag der Wissenschaften 1988
• Alfio Quarteroni, Riccardo Sacco, Fausto Saleri: Numerische Mathematik 1, Springer-Verlag 2002, ISBN 3540678786