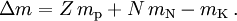Massedefekt

Als Massendefekt (auch Massenverlust) bezeichnet man in der Kernphysik den Unterschied zwischen der Summe der Massen aller Nukleonen (Protonen und Neutronen), aus denen ein Atomkern besteht, und der tatsächlich gemessenen (stets kleineren) Masse des Atomkerns. Auch die Summe von Kernmasse und der Massen der Elektronen in der Atomhülle in einem neutralen Atom ist größer als die gemessene Atommasse. Dieser Massendefekt ist jedoch wesentlich geringer als der Massendefekt beim Zusammenfügen von Protonen und Neutronen und wird meist vernachlässigt.

Der Massendefekt widerlegt die Unterstellung der klassischen Physik, die Masse sei in allen Vorgängen erhalten.

Massendefekt und Bindungsenergie

Der Massendefekt lässt sich mit der Erkenntnis der relativistischen Physik erklären, dass man an der Masse die Energie des ruhenden Teilchens ablesen kann: die Bindungsenergie der Nukleonen vermindert die Summe der Ruheenergien der einzelnen Kernbausteine. Somit ist die beim Bau eines Atoms freigesetzte Bindungsenergie der Nukleonen diejenige Energie, die dem Massendefekt nach der Beziehung E_B = Δmc² äquivalent ist.

Je größer der Massendefekt ist, desto stabiler ist der Atomkern, da mehr Energie zu seiner Zerlegung aufgewendet werden muss.

Massendefekt bei verschiedenen Massenzahlen

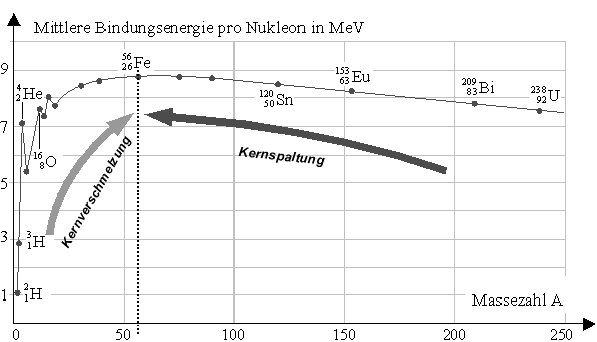
Der gesamte Massendefekt steigt mit der Anzahl der beteiligten Nuklide. Wenn man den durchschnittlichen Massendefekt pro Nukleon bestimmt (z. B. durch Messungen mittels Massenspektrometern) und daraus die Bindungsenergie (in der Einheit MeV) berechnet, so ergibt sich folgender Zusammenhang mit der Massenzahl, d. h. der Zahl der Nukleonen:

Die höchsten Massendefekte pro Nukleon finden sich bei Nukliden, deren Atomkern aus ungefähr 60 Nukleonen besteht, eine ganze Reihe von Isotopen haben hier fast identische Werte. Das stabilste aller Nuklide ist das häufigste Eisenisotop Fe-56.

Wenn leichte Nuklide, die deutlich links von diesem Massendefekt-Maximum liegen, durch Kernfusion (Kernverschmelzung) eine höhere Nukleonenzahl erreichen, dann erhöht sich der Massendefekt pro Nukleon, somit wird diese nun zusätzlich fehlende Masse in Energie umgewandelt, welche genutzt werden kann.

Schwere Kerne (rechts vom Massendefekt-Maximum), die durch Kernspaltung in zwei Nuklide im mittleren Bereich zerlegt werden, setzen ebenfalls Energie frei.

Bei Kernen der Massenzahlen von etwa 60 ist eine Umwandlung von Masse in Energie im nennenswertem Umfang weder durch Spaltung noch durch Verschmelzung möglich.

Eine Energie freisetzende Umwandlung erfolgt somit immer „in Richtung zum Maximum des Massendefekts“, also mit ansteigender Kurve. Rechts des Maximums, also mit schweren Elementen wie zum Beispiel Uran, wird daher durch Kernspaltung Masse in Energie umgewandelt, durch Kernfusion geht das dagegen grundsätzlich nur links des Maximums, also mit leichten Elementen wie zum Beispiel Wasserstoff. Allerdings nutzen die praktisch (in Gestirnen und in der Energietechnologie) wichtigen Fusionsreaktionen meist das in der Abbildung sichtbare starke lokale Maximum des Massendefekts beim Helium-Isotop ⁴He aus.

Berechnung

Der Massendefekt eines Atomkerns ergibt sich aus der Differenz der Masse seiner Protonen (Ordnungszahl = Kernladungszahl Z) und Neutronen (Neutronenanzahl N) und seiner tatsächlichen Kernmasse m_K:

$\Delta m = Z \, m_\mathrm{p} + N \, m_\mathrm{N} - m_\mathrm{K} \,.$

In guter Näherung kann Δm auf halbempirischer Basis mittels der Bethe-Weizsäcker-Formel auf der Grundlage des Tröpfchenmodells des Atomkerns berechnet werden.

In der Praxis wird der Massendefekt nicht für den isolierten Atomkern, sondern für das gesamte, ungeladene Atom des jeweiligen Nuklids angegeben. Dies hat experimentelle Gründe: Vollständig ionisierte, also „nackte“ Atomkerne lassen sich nur schwer gewinnen und handhaben, weil sie mit ihrer hohen positiven elektrischen Ladung sofort Elektronen aus der Umgebung einfangen. Die genaue Messung ihrer Masse wäre daher kaum möglich, besonders bei schweren Elementen (Elementen hoher Ordnungszahl) mit ihrer entsprechend besonders hohen Ladung.

In der Literatur finden sich häufig Rechenbeispiele für vergleichsweise einfache Kerne, in denen der Kern ohne Elektronenhülle betrachtet wird. In Tabellen wird jedoch in der Regel der Massendefekt bezogen auf das ganze neutrale Atom angegeben.

Beispiele

Die Masse eines Protons beträgt m_p = 1,007276 Atomare Masseneinheiten (u), die eines Neutrons m_n = 1,008665 u. Der Kern von Helium ⁴He besteht aus zwei Protonen und zwei Neutronen; die Summe aus deren Ruhemassen wäre 4,03188 u, die Ruhemasse des ⁴He-Kerns beträgt jedoch nur 4,00151 u. Der Massendefekt beträgt hier also etwa 0,76 % der Ausgangsmasse.

Der Kern von ²³⁸Uran besteht aus 92 Protonen und 146 Neutronen. Diese besitzen zusammen die Masse 239,9344 u, der ²³⁸Uran-Kern jedoch nur 238,0003 u, dies entspricht einem Massendefekt von 0,806 % der Ausgangsmasse. Dieser Massenunterschied lässt sich nicht komplett in Energie umwandeln, denn bei der Kernspaltung entstehen keine 92 Protonen und 146 Neutronen. Tatsächlich wird bei der Kernspaltung etwa ein Zehntel dieser Energie freigesetzt, sie entspricht der Differenz aus dem Massendefekt des ²³⁵Uran und der beiden Massendefekte der entstehenden Kerne.