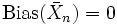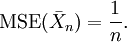Mean squared error

Zwei Schätzfunktionen: Die Wahl einer verzerrten Statistik kann hinsichtlich ihrer erwarteten Abweichung vom echten Wert gegenüber einer unverzerrten vorteilhaft sein.

Die mittlere quadratische Abweichung oder mittlerer quadratischer Fehler (engl. mean squared error und daher mit "MSE" abgekürzt) ist ein Begriff der mathematischen Statistik. Mit der mittleren quadratischen Abweichung kann die Abweichung eines Schätzers von dem zu schätzenden Wert (oder allgemeiner: von Funktionalen von ihnen) berechnet werden.

Definition

Es seien 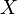$X\;$ eine Zufallsvariable und f eine messbare Funktion. Wenn g geschätzt werden soll, dann ist die mittlere quadratische Abweichung eines Schätzers 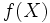$f(X)\;$ für g wie folgt definiert:

$\mbox{MSE}(f,g) = E [ \| f(X) - g \|^2]\;$

Im klassischen Falle reellwertiger Funktionen heißt das dann:

$\mbox{MSE}(f,g) = \mbox{Bias}^2(f(X))+ \mbox{Var}(f(X)). \;$

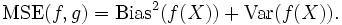
Dabei ist die Verzerrung $\mbox{Bias}(f(X)) := E[f(X) - g] \;$ und verschwindet also im Fall der Erwartungstreue (der MSE entspricht dann der Varianz).

Interpretation

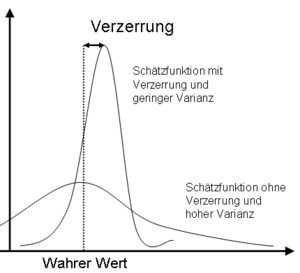
Eine geringe mittlere quadratische Abweichung bedeutet im klassischen Fall, dass gleichzeitig Bias und Varianz des Schätzers klein sind. Man befindet sich mit dem Schätzer also im Mittel in der Nähe des zu schätzenden Funktionals (geringer Bias) und weiß gleichzeitig, dass die Schätzwerte wenig streuen (geringe Varianz) und mit großer Wahrscheinlichkeit auch in der Nähe ihres Erwartungswerts liegen.

Mit dem MSE ist es daher möglich, Schätzverfahren miteinander zu vergleichen. Die Idee ist, dass es vorteilhaft sein kann, einen leicht verzerrten Schätzer zu bevorzugen, der dafür eine wesentlich kleinere Varianz besitzt. Dabei gilt das Schätzverfahren mit dem kleineren MSE in der Regel als das bessere.

Problematisch ist, dass der MSE vom zu schätzenden, unbekannten Grundgesamtheitsparameter abhängt.

Beispiel

Ein typischer Fall ist die Schätzung des Mittelwerts einer Normalverteilung. Wir nehmen an, dass Zufallsvariablen 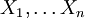$X_1, \ldots X_n\;$ existieren, die jeweils normalverteilt mit unbekanntem Erwartungswert γ und Varianz 1 sind. Der klassische Schätzer ist das Stichprobenmittel 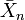$\bar{X}_n$. Hier ist die Verzerrung null:

$\mbox{Bias}(\bar{X}_n) = 0$

da der empirische Mittelwert erwartungstreu für γ ist. Da 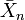$\bar{X}_n$ selbst normalverteilt mit Erwartungswert γ und Varianz $\frac 1n$ ist, folgt

$\mbox{MSE}(\bar{X}_n) = \frac 1n.$

Ausweitung auf beliebige Verlustfunktionen

Eine Verallgemeinerung der mittleren quadratischen Abweichung ergibt sich, wenn man in der Definition an Stelle des quadratischen Abstandes von Schätzer und unbekanntem Funktional eine beliebige andere Funktion 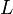$L\;$ ersetzt, die

• symmetrisch ist,
• Werte in 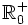$\mathbb R^{+}_{0}$ besitzt und
• in beiden Komponenten konvex ist.

Abbildungen dieser Art heißen Verlustfunktion, das Risiko eines Schätzers 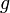$g\;$ ist dann definiert als

$\mbox{R}_\vartheta(g) = E_{\vartheta}[L(g(X), \gamma (\vartheta))].$