- Mehrfachwinkelformeln
-
Dies ist eine Formelsammlung zu dem mathematischen Teilgebiet der Trigonometrie.
Dreieckberechnung
Die folgende Liste enthält die meisten bekannten Formeln aus der Trigonometrie in der Ebene. Die meisten dieser Beziehungen verwenden trigonometrische Funktionen.
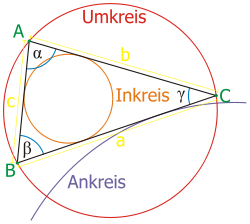
Dabei werden die folgenden Bezeichnungen verwendet: Das Dreieck ABC habe die Seiten a = BC, b = CA und c = AB, die Winkel α, β und γ bei den Ecken A, B und C. Ferner seien r der Umkreisradius, ρ der Inkreisradius und ρa, ρb und ρc die Ankreisradien (und zwar die Radien der Ankreise, die den Ecken A, B bzw. C gegenüberliegen) des Dreiecks ABC. Die Variable s steht für den halben Umfang des Dreiecks ABC:
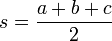 . Schließlich wird die Fläche des Dreiecks ABC mit F bezeichnet. Alle anderen Bezeichnungen werden jeweils in den entsprechenden Abschnitten, in denen sie vorkommen, erläutert.
. Schließlich wird die Fläche des Dreiecks ABC mit F bezeichnet. Alle anderen Bezeichnungen werden jeweils in den entsprechenden Abschnitten, in denen sie vorkommen, erläutert.Winkelsumme
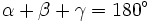 .
.
Sinussatz
Formel 1:
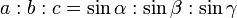 (Verhältnisgleichung)
(Verhältnisgleichung)
Formel 2: wenn α = 90°
Kosinussatz
Formel 1:
Formel 2: wenn α = 90°
Projektionssatz
Die Mollweideschen Formeln
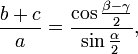
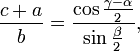
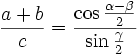
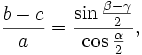
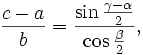
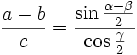
Tangenssatz
Formel 1:
Analoge Formeln gelten für (c + a)/(c - a) und (a + b)/(a - b).
Formel 2: wenn α = 90°
Formeln mit dem halben Umfang
Im folgenden bedeutet s immer die Hälfte des Umfangs des Dreiecks ABC, also
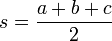 .
.Flächeninhalt und Umkreisradius
Der Flächeninhalt des Dreiecks ABC wird hier mit F bezeichnet (nicht, wie heute üblich, mit A, um eine Verwechselung mit der Dreiecksecke A auszuschließen):
Den Umkreisradius des Dreiecks ABC bezeichnen wir mit r.
(Es ist zu beachten, dass die hier benutzten Bezeichnungen r, ρ, ρa, ρb, ρc für den Umkreisradius, den Inkreisradius und die drei Ankreisradien von der vorwiegend im englischsprachigen Raum verbreiteten Bezeichnungsweise abweichen, bei der dieselben Größen R, r, ra, rb, rc genannt werden.)
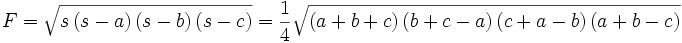
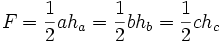 , wobei ha, hb und hc die Längen der von A, B bzw. C ausgehenden Höhen des Dreiecks ABC sind.
, wobei ha, hb und hc die Längen der von A, B bzw. C ausgehenden Höhen des Dreiecks ABC sind.
Erweiterter Sinussatz:
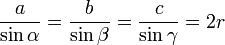
In- und Ankreisradien
In diesem Abschnitt werden Formeln aufgelistet, in denen der Inkreisradius ρ und die Ankreisradien ρa, ρb und ρc des Dreiecks ABC vorkommen.
Wichtige Ungleichung:
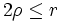 ; Gleichheit tritt nur dann ein, wenn Dreieck ABC gleichseitig ist.
; Gleichheit tritt nur dann ein, wenn Dreieck ABC gleichseitig ist.Die Ankreise sind gleichberechtigt: Jede Formel für ρa gilt in analoger Form für ρb und ρc.
Höhen
Die Längen der von A, B bzw. C ausgehenden Höhen des Dreiecks ABC werden mit ha, hb und hc bezeichnet.
Hat das Dreieck ABC einen rechten Winkel bei C (ist also γ = 90°), dann gilt
Seitenhalbierende
Die Längen der von A, B bzw. C ausgehenden Seitenhalbierenden des Dreiecks ABC werden sa, sb und sc genannt.
Winkelhalbierende
Wir bezeichnen mit wα, wβ und wγ die Längen der von A, B bzw. C ausgehenden Winkelhalbierenden im Dreieck ABC.
Allgemeine Trigonometrie in der Ebene
Gegenseitige Darstellung
Die trigonometrischen Funktionen lassen sich in einander umwandeln oder gegenseitig darstellen. Es gelten folgende Zusammenhänge:
(Siehe auch Phasenverschiebungen.)
Mittels dieser Gleichungen lassen sich die drei vorkommenden Funktionen durch eine der beiden anderen darstellen:
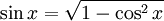
für ![x \in \left[0,\pi \right]=[0^\circ,180^\circ]](/pictures/dewiki/55/73e91ab244a90d9aa94059baa0722580.png)
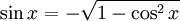
für ![x \in \left[ \pi , 2\pi \right]=[180^\circ,360^\circ]](/pictures/dewiki/98/b7ebd4848a161c4b61688c689882d8cb.png)
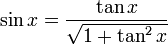
für ![x\in\left[0,\frac{\pi}{2}\right]\cup\left[\frac{3\pi}{2},2\pi\right]
=[0^\circ,90^\circ] \cup [270^\circ, 360^\circ]](/pictures/dewiki/101/e4f15f7f8760c31314fbd137cd09760d.png)
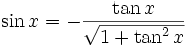
für ![x \in \left[ \frac{\pi}{2}, \frac{3\pi}{2} \right]=[90^\circ,270^\circ]](/pictures/dewiki/49/1a7a299db4fccc4520b71169b7dd0ca0.png)
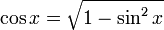
für ![x\in\left[0,\frac{\pi}{2}\right]\cup\left[\frac{3\pi}{2},2\pi\right]
=[0^\circ,90^\circ]\cup [270^\circ,360^\circ]](/pictures/dewiki/101/e4f15f7f8760c31314fbd137cd09760d.png)
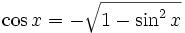
für ![x\in \left[ \frac{\pi}{2} , \frac{3\pi}{2} \right]=[90^\circ ,270^\circ]](/pictures/dewiki/49/1a7a299db4fccc4520b71169b7dd0ca0.png)
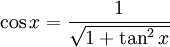
für ![x\in\left[0,\frac{\pi}{2}\right]\cup\left[\frac{3\pi}{2},2\pi\right]
=[0^\circ,90^\circ] \cup [270^\circ,360^\circ]](/pictures/dewiki/101/e4f15f7f8760c31314fbd137cd09760d.png)
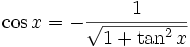
für ![x \in \left[ \frac{\pi}{2},\frac{3\pi}{2} \right]=[90^\circ,270^\circ]](/pictures/dewiki/49/1a7a299db4fccc4520b71169b7dd0ca0.png)
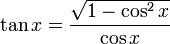
für ![x \in \left[0,\pi \right]=[0^\circ,180^\circ]](/pictures/dewiki/55/73e91ab244a90d9aa94059baa0722580.png)
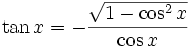
für ![x \in \left[ \pi,2\pi \right]=[180^\circ,360^\circ]](/pictures/dewiki/98/b7ebd4848a161c4b61688c689882d8cb.png)
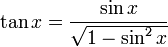
für ![x\in\left[0,\frac{\pi}{2}\right]\cup\left[\frac{3\pi}{2},2\pi\right]
=[0^\circ,90^\circ]\cup [270^\circ,360^\circ]](/pictures/dewiki/101/e4f15f7f8760c31314fbd137cd09760d.png)
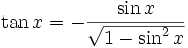
für ![x\in \left[ \frac{\pi}{2} , \frac{3\pi}{2} \right]=[90^\circ,270^\circ]](/pictures/dewiki/49/1a7a299db4fccc4520b71169b7dd0ca0.png)
Vorzeichen der Winkelfunktionen
Die Vorzeichen von cot, sec und csc stimmen überein mit denen ihrer Kehrwertfunktionen tan, cos bzw. sin.
Wichtige Funktionswerte
α ° α (rad) sin α cos α tan α cot α 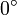
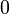
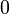
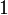
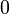
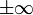
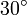
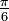
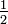
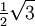
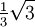
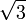
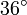
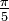
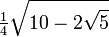
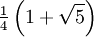
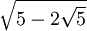
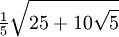
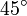
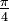
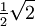
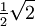
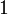
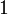
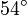
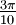
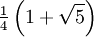
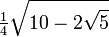
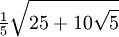
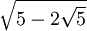
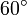
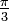
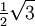
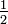
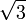
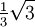
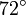
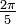
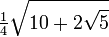
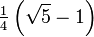
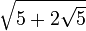
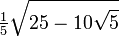
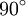
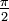
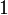
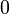
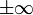
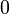
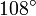
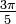
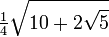
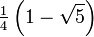
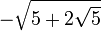
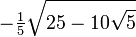
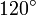
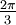
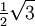
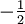
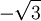
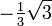
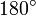
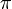
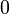
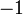
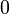
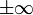
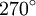
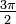
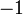
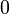
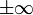
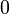
Symmetrien
Die trigonometrischen Funktionen haben einfache Symmetrien:
Phasenverschiebungen
Additionstheoreme
Weiterhin sind die Additionstheoreme nützlich:
Für x = y folgen hieraus die Doppelwinkelfunktionen.
Für
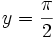 folgen hieraus die Phasenverschiebungen.
folgen hieraus die Phasenverschiebungen.Für die Arkusfunktionen gelten folgende Additionstheoreme[3]
Doppelwinkelfunktionen
Winkelfunktionen für weitere Vielfache
Die Formel für cos(nx) steht über Tn(cosx) = cos(nx)[4] mit den Tschebyschow-Polynomen in Beziehung.
Halbwinkelformeln
Zur Berechnung des Funktionswertes des halben Arguments dienen die Halbwinkelformeln[9]:
Siehe auch: Halbwinkelsatz
Summen zweier trigonometrischer Funktionen (Identitäten)
Aus den Additionstheoremen lassen sich Identitäten ableiten, mit denen die Summe zweier trigonometrischer Funktionen als Produkt aufgefasst werden kann[9]:
Produkte der Winkelfunktionen
Produkte der trigonometrischen Funktionen lassen sich mit folgenden Formeln berechnen[9]:
Potenzen der Winkelfunktionen
Sinus
Kosinus
Tangens
Reduktionsformeln
Es gibt Reduktionsformeln, mit denen man das Argument einer Winkelfunktion in das Intervall [0, 90°] bzw. [0, π/4] bringen kann.
Siehe auch: Zusammenhang mit den Hyperbelfunktionen, Quadrant
Umrechnung in andere trigonometrische Funktionen
Weitere Formeln
Die folgenden Formeln folgen nach längeren Termumformungen aus α + β + γ = 180°, gelten also allgemein für drei beliebige Winkel α, β und γ mit der Eigenschaft α + β + γ = 180°, solange die in den Formeln vorkommenden Funktionen wohldefiniert sind (letzteres betrifft nur die Formeln, in denen Tangens und Kotangens vorkommen).
Sinusoid
Reihenentwicklung
Wie auch sonst in der Analysis werden alle Winkel im Bogenmaß angegeben.
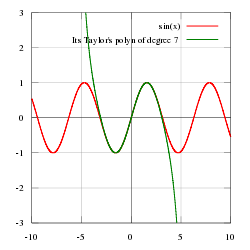
Man kann zeigen, dass der Kosinus die Ableitung des Sinus darstellt und die Ableitung des Cosinus der negative Sinus ist. Hat man diese Ableitungen, kann man die Taylorreihe entwickeln (am einfachsten mit dem Entwicklungspunkt x = 0) und zeigen, dass die folgenden Identitäten für alle x aus den reellen Zahlen gelten. Mit diesen Reihen werden die trigonometrischen Funktionen für komplexe Argumente definiert (Bn bzw. βn bezeichnet dabei die Bernoulli-Zahlen):
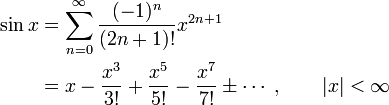
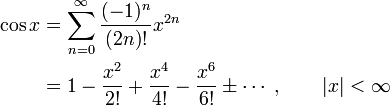
Produktentwicklung
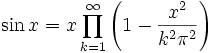
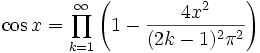
Zusammenhang mit der komplexen Exponentialfunktion
Ferner besteht zwischen den Funktionen sinx, cosx und der komplexen Exponentialfunktion exp(ix) folgender Zusammenhang:
Auf Grund der oben genannten Symmetrien gilt weiter:
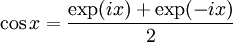
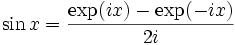
Mit diesen Beziehungen können einige Additionstheoreme besonders einfach und elegant hergeleitet werden.
Einzelnachweise
- ↑ Die Wurzel 2006/04+05, 104ff., ohne Beweis
- ↑ a b Otto Forster Analysis 1 Differential- und Integralrechnung einer Veränderlichen vieweg 1983 Seite 87
- ↑ Milton Abramowitz and Irene Stegun: Handbook of Mathematical Functions, (1964) Dover Publications, New York. ISBN 0-486-61272-4 4.4.32 - 4.4.36
- ↑ Milton Abramowitz and Irene A. Stegun, ebenda 22.3.15
- ↑ Milton Abramowitz and Irene A. Stegun, ebenda 4.3.27
- ↑ Milton Abramowitz and Irene A. Stegun, ebenda 4.3.29
- ↑ I. S. Gradshteyn and I. M. Ryzhik, Table of Integrals, Series, and Products, Academic Press, 5th edition (1994). ISBN 0-12-294755-X 1.333.4
- ↑ I. S. Gradshteyn and I. M. Ryzhik, ebenda 1.331.3 (Bei dieser Formel enthält Gradshteyn/Ryzhik allerdings einen Vorzeichenfehler)
- ↑ a b c d e f g h i j k l m n o I. N. Bronstein, K. A. Semendjajew, Taschenbuch der Mathematik, B. G. Teubner Verlagsgesellschaft Leipzig. 19. Auflage 1979. 2.5.2.1.3
- ↑ Milton Abramowitz and Irene A. Stegun, ebenda 4.3.28
- ↑ Milton Abramowitz and Irene A. Stegun, ebenda 4.3.30
- ↑ I. S. Gradshteyn and I. M. Ryzhik, ebenda 1.335.4
- ↑ I. S. Gradshteyn and I. M. Ryzhik, ebenda 1.335.5
- ↑ I. S. Gradshteyn and I. M. Ryzhik, ebenda 1.331.3
- ↑ I. S. Gradshteyn and I. M. Ryzhik, ebenda 1.321.1
- ↑ I. S. Gradshteyn and I. M. Ryzhik, ebenda 1.321.2
- ↑ I. S. Gradshteyn and I. M. Ryzhik, ebenda 1.321.3
- ↑ I. S. Gradshteyn and I. M. Ryzhik, ebenda 1.321.4
- ↑ I. S. Gradshteyn and I. M. Ryzhik, ebenda 1.321.5
- ↑ I. S. Gradshteyn and I. M. Ryzhik, ebenda 1.323.1
- ↑ I. S. Gradshteyn and I. M. Ryzhik, ebenda 1.323.2
- ↑ I. S. Gradshteyn and I. M. Ryzhik, ebenda 1.323.3
- ↑ I. S. Gradshteyn and I. M. Ryzhik, ebenda 1.323.4
- ↑ I. S. Gradshteyn and I. M. Ryzhik, ebenda 1.323.5
- ↑ Milton Abramowitz and Irene A. Stegun, ebenda 4.3.67
- ↑ Milton Abramowitz and Irene A. Stegun, ebenda 4.3.70
Wikimedia Foundation.

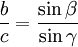
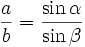
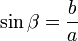
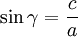
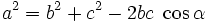
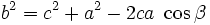
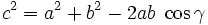
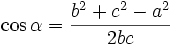
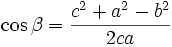
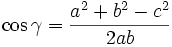
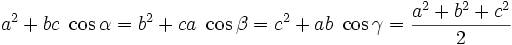
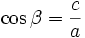
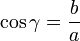
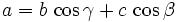
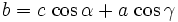
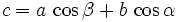
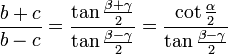
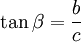
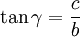
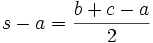
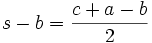
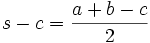
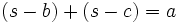
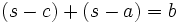
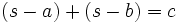
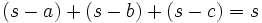
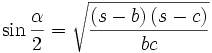
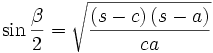
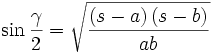
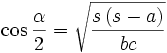
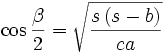
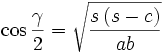
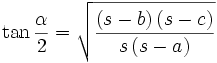
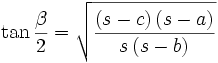
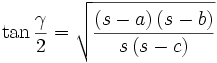
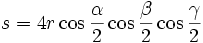
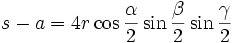
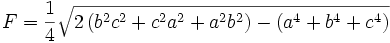
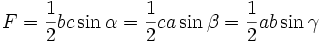
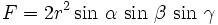
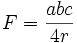
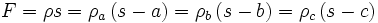
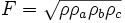
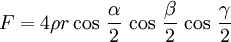
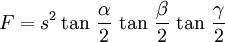
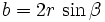
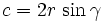
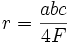
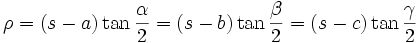
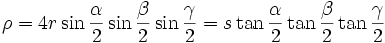
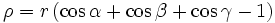
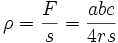
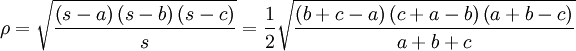
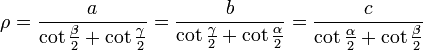
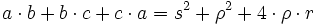
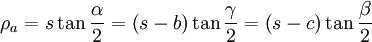
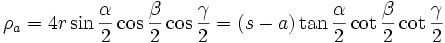
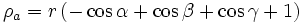
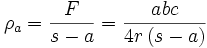
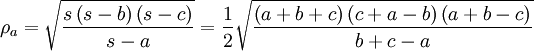
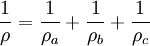
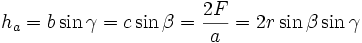
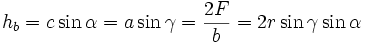
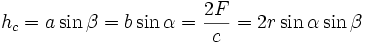
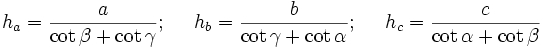
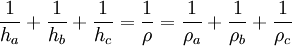
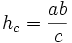
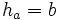
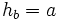
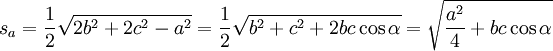
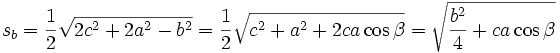
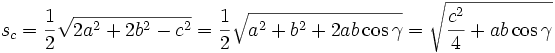
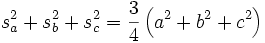
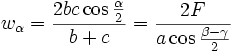
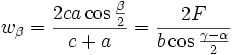
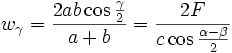
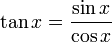
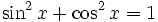
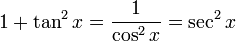
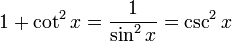
![\sin x > 0 \quad \mathrm{f\ddot ur} \quad x\in \left] 0^{\circ },180^\circ\right[](/pictures/dewiki/101/e6d2a921afdb9e61955fdc1030dcc5ba.png)
![\sin x < 0 \quad \mathrm{f\ddot ur} \quad x\in \left] 180^{\circ },360^\circ\right[](/pictures/dewiki/51/3557af3c65f2dc42072814668d149eea.png)
![\cos x > 0 \quad \mathrm{f\ddot ur} \quad x\in \left[ 0^\circ,90^\circ\right[ \cup \left] 270^\circ,360^\circ\right]](/pictures/dewiki/50/2d7800239c5566e27925031e91a6d76d.png)
![\cos x < 0 \quad \mathrm{f\ddot ur} \quad x\in \left] 90^{\circ },270^\circ\right[](/pictures/dewiki/51/31247bd3573944a9171231303ea4a321.png)
![\tan x > 0 \quad \mathrm{f\ddot ur} \quad x\in \left] 0^{\circ },90^\circ\right[ \cup \left] 180^\circ,270^\circ\right[](/pictures/dewiki/100/d0cee2848f750a9cebde32a51e3e9fc9.png)
![\tan x < 0 \quad \mathrm{f\ddot ur} \quad x\in \left] 90^{\circ },180^\circ\right[
\cup \left] 270^\circ,360^\circ\right[](/pictures/dewiki/56/88822686035e184ac3bfd7dbffd58cb5.png)
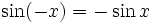
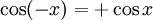
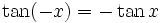
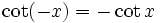
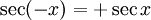
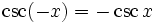
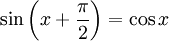
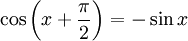
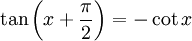
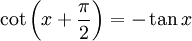
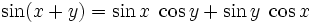
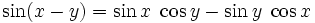
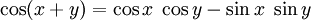
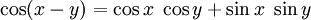
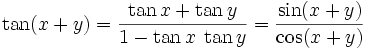
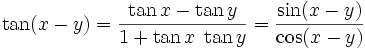
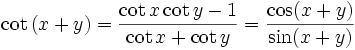
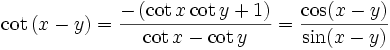
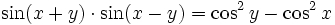
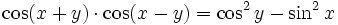
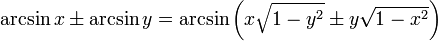
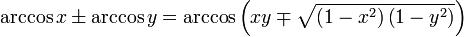
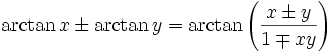
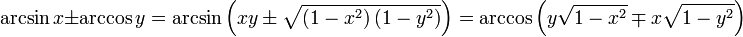
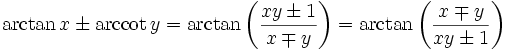
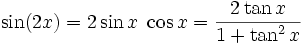
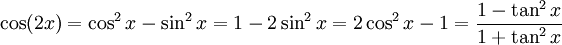
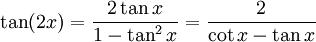
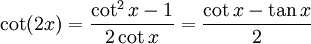
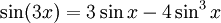
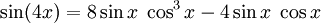
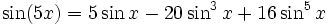
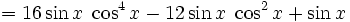
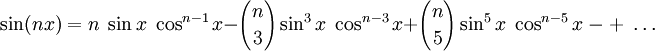
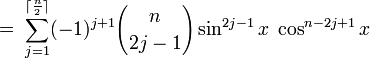
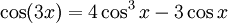
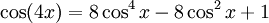
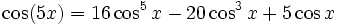
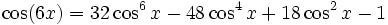
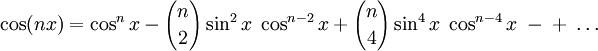
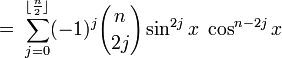
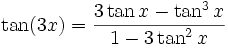
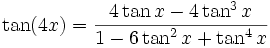
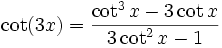
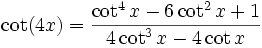
![\sin \frac{x}{2} = \pm \sqrt{\frac{1-\cos x}{2}} \quad \mathrm{f\ddot ur} \quad x\in \left[ 0^{\circ };\;360^{\circ }\right]](/pictures/dewiki/53/523fe05e10fb5b6824548acf6962ec02.png)
![\cos \frac{x}{2} = \pm \sqrt{\frac{1+\cos x}{2}} \quad \mathrm{f\ddot ur} \quad x\in \left[ -180^{\circ };\;180^{\circ }\right]](/pictures/dewiki/102/f29e6e1b8154026ae21bb706da08626a.png)
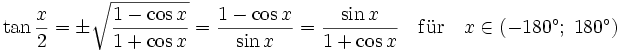
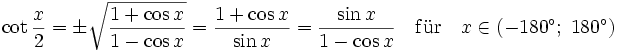
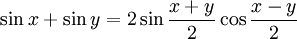
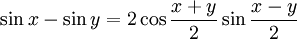
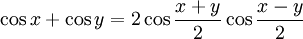
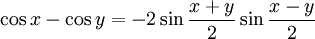
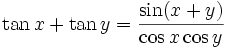
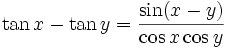
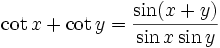
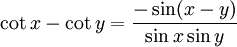
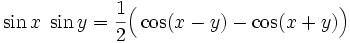
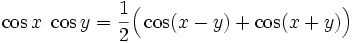
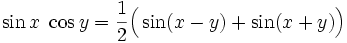
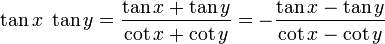
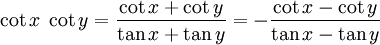
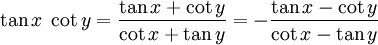
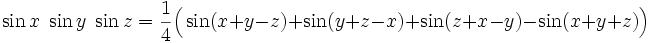
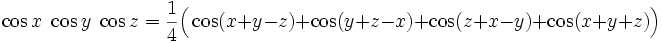
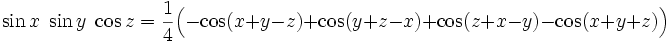
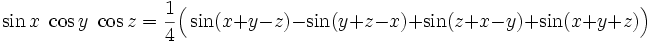
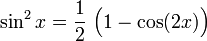
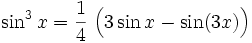
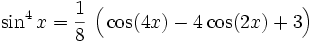
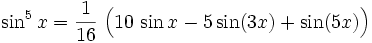
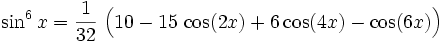
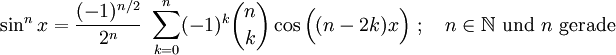
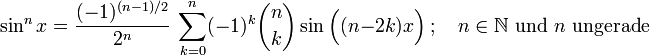
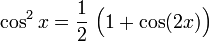
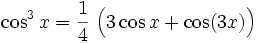
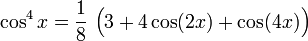
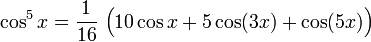
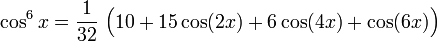
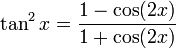
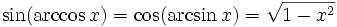
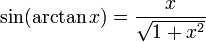
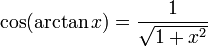
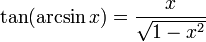
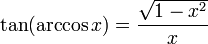
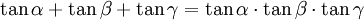
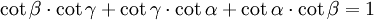
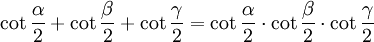
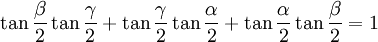
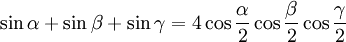
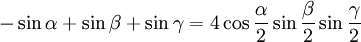
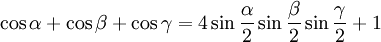
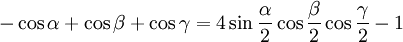
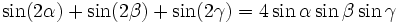
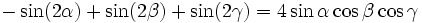
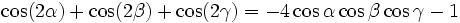
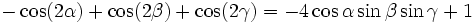
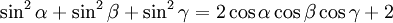
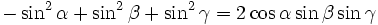
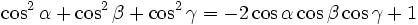
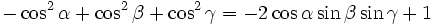
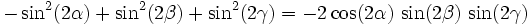
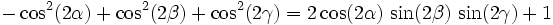
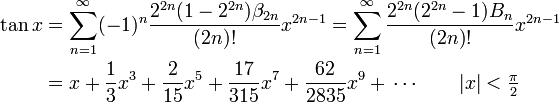
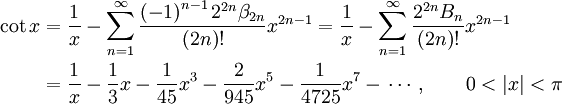
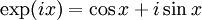 (
(