- Meßunsicherheit
-
Die Messunsicherheit des Schätzwertes oder Schätzers einer physikalischen Größe grenzt einen Wertebereich ein, innerhalb dessen der wahre Wert der Messgröße liegt. Eine Wahrscheinlichkeit dazu ist nicht angebbar. Das Ergebnis einer Messung ist erst durch Schätzer und Messunsicherheit definiert. Die Messunsicherheit ist positiv, sie wird ohne Vorzeichen angegeben. Messunsicherheiten sind selbst Schätzer. Andere Bezeichnungen für Messunsicherheit sind laut DIN 1319-3 Standardmessunsicherheit, Standardunsicherheit oder schlicht Unsicherheit. Wird die Standardunsicherheit als Standardabweichung ausgedrückt, so sind auch diese beiden Begriffe synonym verwendbar. Früher wurde für Unsicherheit der Begriff Fehler verwendet.
Sinn und Ziel des Schätzens von Messunsicherheiten ist es, Intervalle festzulegen, die die wahren Werte der Messgrößen einschließen oder „lokalisieren“ sollen.
In aller Regel legt die Messunsicherheit einen zum Schätzwert der Messgröße symmetrisch liegenden Wertebereich fest, wobei der Schätzwert von bekannten systematischen Fehlern befreit worden ist. Bekannte systematische Messfehler sind nicht Gegenstand der Fehlerrechnung. Das Messergebnis ist durch einen Ausdruck der Form
- Schätzwert
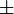Messunsicherheit
gegeben. Der so definierte Bereich (das Intervall) hat die Länge der doppelten Messunsicherheit.
Eine weitere Schreibweise ist die nachgestellte Angabe der Messunsicherheit in Klammern. Dabei geben die in den Klammern stehenden Ziffern die Unsicherheit der letzten Ziffern des Messwertes an.
Beispiel: 0,8543(24) entspricht 0,8543
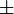0,0024Inhaltsverzeichnis
Metrologische Bedeutung von Messunsicherheiten
Die Messunsicherheiten in Wissenschaft und Technik sollen drei Aufgaben erfüllen.
- Sie sollen Messresultate objektivieren, indem sie festlegen, in welchem Intervall der wahre Wert der Messgröße zu erwarten ist. Nach klassischer Diktion waren das Konfidenzintervalle, deren Längen von der Höhe eines Vertrauensniveaus abhingen. Die klassische Fehlerrechnung muss um sogenannte unbekannte systematische Messfehler erweitert werden. Daher kann der Messunsicherheit nicht auf dieselbe Weise eine Wahrscheinlichkeit zugewiesen werden, wie es bei ausschließlich statistischen Fehlern möglich ist.
- Das auf diese Weise geschaffene Netz physikalischer Konstanten muss in sich widerspruchsfrei sein, d. h. berechnete man anhand einer gegebenen Verknüpfungsfunktion aus einer Teilmenge von Konstanten eine andere, numerisch bereits bekannte Konstante, so muss die aus der Fehlerfortpflanzung hervorgehende Messunsicherheit wiederum den wahren Wert dieser Konstanten lokalisieren. Messunsicherheiten müssen also der Forderung nach „Rückverfolgbarkeit der wahren Werte“ genügen.
- Messunsicherheiten sollen Theorie und Experiment objektiv vergleichbar machen. Sie werden als Mittel verwendet, eine zur Debatte stehende neue Theorie entweder zu verwerfen oder sie zu bestätigen.
Hinterfragung der Fehlerrechnung
Die „klassische“ Gauß'sche Fehlerrechnung behandelt ausschließlich zufällige Messfehler. Indessen hatte schon Gauß auf die Existenz und Bedeutung so genannter unbekannter systematischer Messfehler hingewiesen. Das sind zeitkonstante, nach Betrag und Vorzeichen unbekannte Störgrößen, die in der Regel in einer mit den zufälligen Fehlern vergleichbaren Größenordnung liegen. Unbekannte systematische Messfehler müssen mit Hilfe von Intervallen eingegrenzt werden.
Der heutige Mainstream der Metrologie interpretiert die Prozedur des Schätzens der Messunsicherheit als „technische Vorschrift“, die einheitlich zu praktizieren ist. Im Bereich des gesetzlichen Messwesens und des Kalibrierdienstes in Deutschland wird empfohlen, Messunsicherheiten nach DIN festzulegen. Dieser Leitfaden zur Angabe der Unsicherheit beim Messen entspricht der europäischen Vornorm ENV 13005, welche die Empfehlung der ISO übernimmt; er hat auch unter dem Akronym „GUM“ Bekanntheit erlangt.
Siehe auch
- Guide to the Expression of Uncertainty in Measurement
- Fehler
- Fehlerrechnung
- Messabweichung
- Messgerätefehler
Literatur
- DIN 1319 „Grundlagen der Messtechnik“ (Teil 1: Grundbegriffe [Ausgabe: 1995-01] , Teil 2: Begriffe für Messmittel [Ausgabe: 2005-10], Teil 3: Auswertung von Messungen einer einzelnen Meßgröße, Meßunsicherheit [Ausgabe: 1996-05], Teil 4: Auswertung von Messungen; Meßunsicherheit [Ausgabe: 1999-02])
- DIN, Deutsches Institut für Normung e. V. (Hrsg.): Leitfaden zur Angabe der Messunsicherheit beim Messen. 1. Auflage. Beuth Verlag GmbH, Berlin 1995, ISBN 3-410-13405-0
- DIN V ENV 13005:1999-06, Ausgabe 1999-06 „Leitfaden zur Angabe der Unsicherheit beim Messen“ Deutsche Fassung ENV 13005:1999, Beuth Verlag GmbH, Berlin
- Guide to the Expression of Uncertainty in Measurement, ISO, Internationale Organisation für Normung
- Weise, Klaus; Wöger, Wolfgang: Meßunsicherheit und Meßdatenauswertung. Weinheim: Wiley-VCH 1999. ISBN 3-527-29610-7
Weblinks
GUM
- Allgemeinverständliche Erläuterung der Messunsicherheit
- Guidelines for Evaluating and Expressing the Uncertainty of NIST Measurement Results
Kritik am GUM und Alternativer Ansatz
- Schätzwert
Wikimedia Foundation.
