Mischkreuz

Das Mischungskreuz ist eine mathematische Methode, um Konzentrationen und Mengenverhältnisse zu errechnen, die sich beim Mischen gelöster Chemikalien, Säuren oder Laugen unterschiedlicher Konzentration ergeben. Das Mischungskreuz oder auch Andreaskreuz ist eine Methode, mit der man die Mengenanteile berechnen kann, die man benötigt, um aus zwei Stammlösungen, d. h. Lösungen mit bekannten Konzentrationen, eine Lösung mit einer bestimmten Zielkonzentration zu erzeugen. Das Mischungskreuz lässt sich aus der Richmannschen Mischungsregel ableiten.

Die Berechnungen über das Mischungskreuz funktionieren nur mit Massen. Wenn man mit Volumina rechnen möchte, muss man vorher die einzelnen Volumina mit Hilfe der Dichte in eine Masse umrechnen. Man erhält auch als Ergebnis eine Masse. Diese lässt sich mit der Dichte (bzw. über eine Prozentrechnung) wieder in ein Volumen umrechnen (Dichte = Masse/Volumen = [g/ml], [kg/l]).

Anwendung

Mischen von Flüssigkeiten

Mischungskreuz

Auf der linken Seite des Mischungskreuzes werden die bekannten Ausgangskonzentrationen der Flüssigkeiten eingetragen. An den Kreuzungspunkt schreibt man die gewünschte Zielkonzentration der Mischung. Nun bildet man die Differenz aus der bekannten Konzentration links oben und der gewünschten Zielkonzentration in der Mitte und notiert das Ergebnis rechts unten. Dann bildet man die Differenz aus der bekannten Konzentration links unten und der gewünschten Zielkonzentration in der Mitte und schreibt das Ergebnis rechts oben auf. Negative Ergebnisse werden ohne Vorzeichen notiert (Betragsrechnung). Auf der rechten Seite des Mischungskreuzes erhält man dann als Ergebnis die Anteile an der Gesamtmasse (nicht am Volumen!), mit denen man die gewünschte Zielkonzentration herstellen kann.

Beispielrechnung:

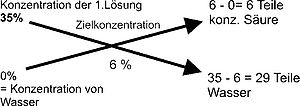
Im Beispiel soll eine 35-prozentige Säure mit Wasser so gemischt werden, 
dass sich eine Ziellösung von 6 % Säureanteil ergibt. 
Wie viel Wasser und wie viel Säure werden benötigt?

Die Ausgangskonzentrationen auf der linken Seite sind 35 % für die Säure und 0 % für das Wasser.
In der Mitte steht die gewünschte Zielkonzentration, in diesem Fall 6 %.  
35 - 6 ergibt 29 Teile, 6 - 0 ergibt 6 Teile, insgesamt sind es 35 Gesamtteile.
Es werden folglich 6 Teile der 35-prozentigen Säure und 29 Teile Wasser benötigt, um eine 6-prozentige Säure herzustellen. 

Volumenberechnung
Sollen 1000 g einer 6-prozentigen Ziellösung hergestellt werden, benötigt man demnach
von der 35-prozentigen Säure:  [1000 g / 35] * 6 = 171 g   
von Wasser: [1000 g / 35] * 29 = 829 g 

An Stelle von 0 % (für die Konzentration von Wasser) könnte links auch ein Wert für
eine 15-prozentige Säure stehen. 
Bei einer Zielkonzentration von 22 % müssten dann 
22 - 15 = 7 Teile 35-prozentige Säure und 
35 - 22 = 13 Teile 15-prozentige Säure gemischt werden.

Legierungen

Das Mischungskreuz eignet sich auch zur näherungsweisen Berechnung der Masseanteile in Metalllegierungen, z.B. der Anteile von Zink und Kupfer in einer Messinglegierung. Wegen der Kristallgitterstruktur von Metallen ergibt die Berechnung mit dem Mischungskreuz nur ungefähre Werte. Die Formeln zur genauen Berechnung finden sich im Artikel Stoffmengenanteil.

Beispielrechnung:

Für die Dichte einer Messinglegierung wurde durch Wiegen und Volumenberechnung der
Wert 8,32 g/cm³ ermittelt. 
Reines Zink besitzt nach Tabelle eine Dichte von 6,97 g/cm³ und Kupfer eine Dichte von 8,61 g/cm³. 
Auf der linken Seite des Mischungskreuzes setzt man die "Ausgangskonzentrationen" 
6,97 (für reines Zink) und 8,61 (für reines Kupfer) ein. 
In die Mitte setzt man den Mischungswert 8,32 für Messing als Zielzahl ein.
Nun wird diagonal subtrahiert:
Subtrahiert man 8,32 von 8,61 ergibt sich 0,29 -- sind 29 Teile Zink
Subtrahiert man 8,32 von 6,97 ergibt sich 1,35 -- sind 135 Teile Kupfer.
29 Teile + 135 Teile = 164 Teile = Gesamtmasse = 100 %
29 Teile entsprechen somit 17,7 % (=Zink). 135 Teile entsprechen 82,3 % (= Kupfer)
Die vorhandene Messinglegierung besteht demnach aus ca. 18 % Zink und 82 % Kupfer.