Mittelpunkregel

Mittelpunktsregel

Die Mittelpunktregel (auch Rechteckregel) ist ein numerisches Verfahren zur näherungsweisen Berechnung von Integralen. Man nimmt dabei den Mittelpunkt des Intervalls [a;b] und multipliziert den Funktionswert an dieser Stelle mit der Intervallbreite (b-a) um das Integral zu bekommen:

$\int_{a}^{b}f(x) dx \approx f\left(\frac{a+b}{2} \right) \cdot (b-a)$.

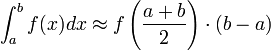Bei der zusammengesetzten Mittelpunktsregel wird nun das Intervall [a;b] in n Teilintervalle aufgeteilt. Anschließend führt man die Mittelpunktsregel für jedes der Teilintervalle aus und summiert die Flächen auf.

Beispiel

Es sei eine Funktion f(x) = lnx im Intervall [2;6] zu integrieren. Dazu wäre die Berechnung des Integrals 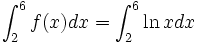$\int_2^6 f(x) dx = \int_2^6 \ln x dx$ nötig.

Rechteckverfahren

1. Zerlegung des Intervalls [2;6] in vier Teilintervalle: [2;3], [3;4], [4;5] und [5;6] mit den Intervallmitten 2,5, 3,5, 4,5 und 5,5.
2. Berechnung von: $\frac{6-2}{4} \cdot (f(2,5) + f(3,5) + f(4,5) + f(5,5)) = \frac{4}{4} (\ln 2,5 + \ln 3,5 + \ln 4,5 + \ln 5,5) \approx 0,9163 + 1,2528 + 1,5041 + 1,7047 = 5,3779$
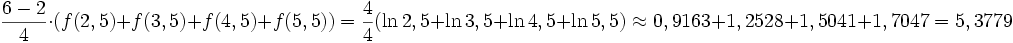
3. Es gilt also $\int_2^6 f(x) dx \approx 5,3779$

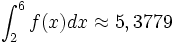
Die analytische Lösung ist: $\int \ln x dx = x \ln x - x + C$

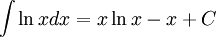
Demnach ist $\int_2^6 f(x) dx = 5,3642...$

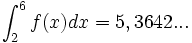
Beispiel Programmcode

Ein BASIC-Code für den Taschenrechner TI 89 bzw. 92:

Prgm mittelpr(a,b,n)

(C)n ist anzahl der teilintervalle
(C)a ist untere grenze
(C)b ist obere grenze

ClrIO
Local  erg,h,j

(b-a)/(n+2)->h

2*h*Sigma(f(a+(2*j+1)*h),j,0,ceiling(n/2))->erg

Disp  {"result",erg}

EndPrgm

Siehe auch

• Numerische Integration

Weblinks

• Numerische Integration Ein Java Applet zur Darstellung verschiedener Integrationsmethoden