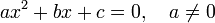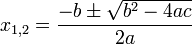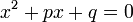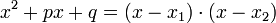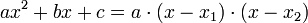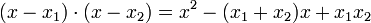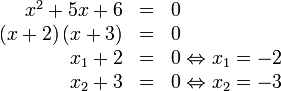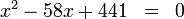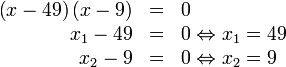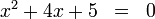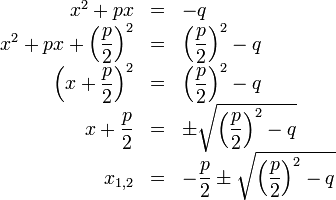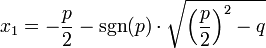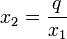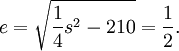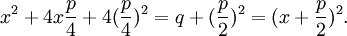Mondscheinformel

Unter einer quadratischen Gleichung versteht man eine mathematische Gleichung der Form

ax² + bx + c = 0.

Dabei sind a,b,c Parameter und x die Unbekannte. Die linke Seite dieser Gleichung ist also ein beliebiges Polynom des Grades 2. Geometrisch beschreibt die quadratische Gleichung die Nullstellen einer quadratischen Funktion, also die x-Koordinaten der Schnittpunkte des Funktionsgraphen (der eine Parabel ist) mit der x-Achse in der x-y-Ebene.

Allgemeine Form und Normalform

Die allgemeine Form der quadratischen Gleichung lautet

$ax^2 + bx + c = 0 \qquad (a, b, c \in \mathbb{R}, \ a \neq 0)$ .

Dabei heißt ax² quadratisches Glied, bx lineares Glied und c Absolutglied (oder auch konstantes Glied) der Gleichung. Die Gleichung ist in Normalform, wenn das quadratische Glied den Koeffizienten 1 hat:

$x^2 + px + q = 0 \qquad (p,q \in \mathbb{R})$ .

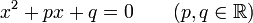Aus der allgemeinen Form lässt sich äquivalent die Normalform gewinnen, indem durch 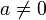$a \neq 0$ dividiert wird.

Beispiel

Gegebene Gleichung:	x2 + 16x + 50 = 5x2 + 4x + 10
Allgemeine Form (alle Terme auf die rechte Seite):	0 = 4x2 − 12x − 40
Normalform:	x2 − 3x − 10 = 0

Lösungen der quadratischen Gleichung

Eine Lösung der quadratischen Gleichung ist eine Zahl, die die Gleichung erfüllt, wenn sie für x eingesetzt wird. Jede quadratische Gleichung (mit reellen oder komplexen Koeffizienten) hat zwei Lösungen, auch Wurzeln genannt. Die Lösungen sind im Allgemeinen komplexe Zahlen, also nicht notwendigerweise reelle Zahlen.

Wenn man sich auf die reellen Zahlen beschränkt, gibt es genau drei mögliche Fälle:

1. Es gibt zwei unterschiedliche Lösungen,
2. es gibt eine (doppelte) Lösung, das heißt eine Zahl tritt zweimal als Lösung auf, oder
3. es gibt keine Lösung.

Wenn man sich auf reelle Lösungen beschränkt, sind manche quadratischen Gleichungen somit nicht auflösbar. Es lassen sich immer zwei Lösungen finden, wenn die Betrachtungen auf die komplexen Zahlen ausgedehnt werden.

Sind die Koeffizienten reelle Zahlen, dann sind entweder beide Wurzeln reell oder beide konjugiert komplex.

Lösungsformeln

Zum Finden von Lösungen einer quadratischen Gleichung kann man die quadratische Ergänzung benutzen. Da die quadratische Gleichung stets die gleiche Struktur aufweist, bietet es sich an, eine allgemeinere Formel herzuleiten, die in der Umgangssprache als „Mitternachtsformel“ bezeichnet wird. Es ergeben sich zwei Lösungsformeln. In ihrer allgemeinen Form

$ax^2+bx+c=0, \quad a\neq 0$

hat die quadratische Gleichung die Lösungen

$x_{1,2} = \frac{-b\pm\sqrt{b^2-4ac}}{2a}$

Im normierten Fall, der sich durch Division beider Seiten der Gleichung durch a erreichen lässt,

$x^2+px+q=0 \quad$

lauten die Lösungen nach der p-q-Formel

$x_{1,2} \;=\; - \frac{p}2\pm\sqrt{\left(\frac{p}2\right)^2 - q} \;\ =\;\ - \frac{p}2\pm\sqrt{\frac{p^2}4 - q} \;\ =\;\ - \frac{p}2\pm\frac12\sqrt{p^2 - 4q}$.

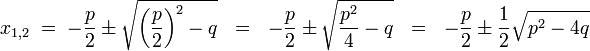Es hängt nur vom Vorzeichen des Radikanden (auch als Diskriminante bezeichnet) p² − 4q bzw. b² − 4ac der oben vorkommenden Wurzel ab, welche Lösungen sich ergeben:

• Ist der Radikand > 0, so ergeben sich zwei verschiedene, reelle Lösungen.
• Ist der Radikand = 0, so ergibt sich eine einzelne, doppelte, reelle Nullstelle (Lösung).
• Ist der Radikand < 0, so ergeben sich zwei verschiedene, konjugiert komplexe Lösungen. In diesem Fall kann man die beiden Lösungen nach der p-q-Formel wie folgt angeben:
  Komplexer Fall: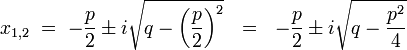  $x_{1,2} \;=\; - \frac{p}{2}\pm i \sqrt{ q - \left(\frac{p}{2}\right)^2 } \;\ =\;\ - \frac{p}{2}\pm i \sqrt{ q - \frac{p^2}{4} }$.

Mit den Lösungen lässt sich das quadratische normierte Polynom in Linearfaktoren zerlegen:

$x^2 + px + q = ( x - x_1 ) \cdot ( x - x_2 )$

und das nicht normierte in

$ax^2 + bx + c = a\cdot( x - x_1 ) \cdot ( x - x_2 )$

Durch Ausmultiplizieren im normierten Fall

$( x - x_1 ) \cdot ( x - x_2 ) = x^2 - (x_1 + x_2) x + x_1 x_2$

und Koeffizientenvergleich erhält man den Satz von Vieta:

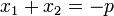$\, x_1 + x_2 = -p$   und   $x_1 \cdot x_2 = q$

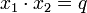
Falls man die Betrachtung im Reellen durchführt und unter der Wurzel einer der Lösungsformeln eine negative Zahl auftritt, so gibt es keine reellen Lösungen, wie man im folgenden Abschnitt am Beispiel der p-q-Formel sieht.

Lösen durch Faktorisieren

Das Faktorisieren ist eine besondere Form zur Lösung quadratischer Gleichungen. Bei vielen Gleichungen bekommt man so schneller eine Lösung. Allerdings kann bei einer nicht lösbaren Gleichung nicht erkannt werden, dass sie nicht lösbar ist. Bei größeren Zahlen kann man die Faktoren nicht immer erkennen. Gelöst werden die Gleichungen dann wie folgt:

Beispiel:

(1)

$\begin{array}{rcl} x^2+5x+6 &amp;amp;amp; = &amp;amp;amp; 0\\ \left(x+2\right)\left(x+3\right) &amp;amp;amp; = &amp;amp;amp; 0\\ x_1+2 &amp;amp;amp; = &amp;amp;amp; 0 \Leftrightarrow x_1 = -2 \\ x_2+3 &amp;amp;amp; = &amp;amp;amp; 0 \Leftrightarrow x_2 = -3\\ \end{array}$

Die eigentliche Schwierigkeit bei diesem Verfahren ist, die Lösungen zu finden. Bei der allgemeinen Form x² + px + q = 0 die richtigen Zahlen zu finden. Die Zahlen x₁ und x₂ müssen addiert -p ergeben und multipliziert q. Bei einigen Gleichungen kann man das Verfahren nicht anwenden, da die Zahlen zu unübersichtlich sind:

(2)

$\begin{array}{rcl} x^2-58x+441 &amp;amp;amp; = &amp;amp;amp; 0\\ \end{array}$

Um auf die Lösung dieser Gleichung zu kommen, muss man ein gutes Zahlengefühl haben oder viel Zeit oder einen Taschenrechner, was das Schriftliche unnötig macht.

$\begin{array}{rcl} \left(x-49\right)\left(x-9\right) &amp;amp;amp; = &amp;amp;amp; 0\\ x_1-49 &amp;amp;amp; = &amp;amp;amp; 0\Leftrightarrow x_1 = 49\\ x_2-9 &amp;amp;amp; = &amp;amp;amp; 0\Leftrightarrow x_2 = 9\\ \end{array}$

(3)

$\begin{array}{rcl} x^2+4x+5 &amp;amp;amp; = &amp;amp;amp; 0\\ \end{array}$

Diese Gleichung hat überhaupt keine Lösung, auch wenn die Zahlen klein und übersichtlich sind. Bei Sonderfällen kann man mit diesem Verfahren auch biquadratische Gleichungen lösen, wenn sie die Form: x⁴ + c² + e = 0 haben

Herleitung der p-q-Formel durch quadratische Ergänzung

Für eine Gleichung der Form:

$x^2+px+q=0 \quad$

ergibt sich durch Umformen nach dem Verfahren der quadratischen Ergänzung:

$\begin{array}{rcl} x^2+px &amp;amp;amp; = &amp;amp;amp; -q\\ x^2+px+\left(\dfrac{p}{2}\right)^2 &amp;amp;amp; = &amp;amp;amp; \left(\dfrac{p}{2}\right)^2-q\\ \left(x+\dfrac{p}{2}\right)^2 &amp;amp;amp; = &amp;amp;amp; \left(\dfrac{p}{2}\right)^2-q\\ x+\dfrac{p}{2} &amp;amp;amp; = &amp;amp;amp; \pm\sqrt{\left(\dfrac{p}{2}\right)^2-q}\\ x_{1,2} &amp;amp;amp; = &amp;amp;amp; -\dfrac{p}{2}\pm\sqrt{\left(\dfrac{p}{2}\right)^2-q} \end{array}$

Anzahl der reellen Nullstellen

Lage der quadratischen Parabeln und Auswirkungen auf die Zahl der Nullstellen

Der Ausdruck unter der Wurzel (die Diskriminante D = b² − 4ac) bestimmt für eine Gleichung mit reellen Koeffizienten, wie viele reellwertige Lösungen die Gleichung hat. Die Grafik zeigt den Zusammenhang zwischen Nullstellen und Diskriminante. Man kann drei Fälle unterscheiden, wobei die in der Grafik dargestellte Normalparabel solche vom Typ 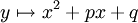$y \mapsto x^2+px+q$ darstellen:

(A) D > 0: Die Parabel hat zwei Schnittpunkte mit der x-Achse, es gibt also zwei verschiedene reelle Nullstellen x₁ und x₂,

(B) D = 0: Die Parabel hat einen Berührpunkt mit der x-Achse. Die Berührstelle x₁ = x₂ ist gleichzeitig auch eine Minimumstelle (falls a > 0) bzw. Maximumstelle (falls a < 0) und der Ausgangsterm der quadratischen Gleichung lässt sich auf die Form 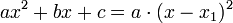$ax^2 + bx + c = a \cdot (x - x_1)^2$ bringen.

(C) D < 0: Die Parabel hat keinen Schnittpunkt mit der x-Achse, es gibt keine reelle Lösung der quadratischen Gleichung.

Numerische Berechnung

Wenn die Lösungen numerisch ermittelt werden und sich um Größenordnungen voneinander unterscheiden, kann durch folgende Variation der obigen Formeln das Problem der Auslöschung vermieden werden:

$x_1 = - \frac{p}{2} - \sgn(p) \cdot \sqrt{ \left(\frac{p}{2}\right)^2 - q }$

$x_2 = \frac{q}{x_1}$

Hierbei hat sgn(p) den Wert −1 für p < 0 und sonst den Wert 1. Die zweite Formel beruht auf dem Satz von Vieta.

Beispiele

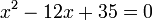
$x^2 - 12x + 35 = 0\$	Beide Lösungen sind positiv: x1 = 7 und x2 = 5
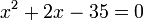
$x^2 + 2x - 35 = 0\$	Die Lösungen haben unterschiedliches Vorzeichen: x1 = −7 und x2 = 5
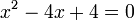
$x^2 - 4x + 4 = 0\$	Die Diskriminante ist D = 0. Die (doppelte) Lösung ist x = 2.
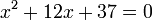
$x^2 + 12x + 37 = 0\$	Es gibt keine reellen Lösungen, denn die Diskriminante ist negativ. Die komplexen Lösungen ergeben sich zu x1 = −6 + i und x2 = −6 − i. Hierbei bezeichnet i die Imaginäre Einheit.

(Reelle) Lösung mit Zirkel und Lineal

Man macht sich bei der Lösung mit Zirkel und Lineal die Satzgruppe von Vieta zu nutze, von deren Richtigkeit man sich durch einfaches Ausrechnen überzeugt:

$x_1\cdot x_2= \left (- \frac{p}{2}+\sqrt{ \left(\frac{p}{2}\right)^2 - q }\right )\cdot \left ( -\frac{p}{2}-\sqrt{ \left(\frac{p}{2}\right)^2 - q }\right )= \left ({p\over 2}\right )^2 - \left ( \left ({p\over 2}\right )^2 -q \right ) = +q$,

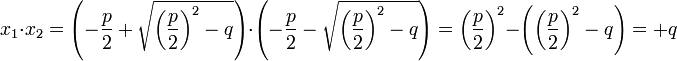sowie

$x_1+ x_2= \left (- \frac{p}{2}+\sqrt{ \left(\frac{p}{2}\right)^2 - q }\right )+ \left ( -\frac{p}{2}-\sqrt{ \left(\frac{p}{2}\right )^2-q}\right )= -2\cdot{p\over 2} = -p$.

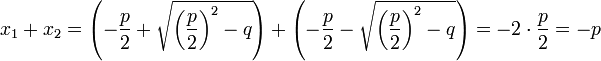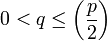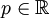Im ersten Falle seien $0 &amp;amp;lt; q \leq \left ( {p \over 2} \right )$ und $p\in \mathbb{R}$ gegeben. Wir bezeichnen mit p nun die Hypotenuse eines rechtwinkligen Dreiecks mit der Länge 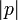$\vert p \vert$. Schlägt man den Thaleskreis über p und sucht auf diesem die Punkte mit Abstand 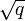$\sqrt{q}$, so teilt jeweils deren Lot auf p die Seite p im Verhältnis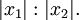 $\vert x_1 \vert : \vert x_2 \vert.$

Zur Konstruktion ermittle man zunächst 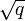$\sqrt{q}$, indem man eine Strecke der Länge q + 1 abtrage, darüber den Thaleskreis schlage und diese Strecke im Verhältnis q:1 durch eine Senkrechte teile. Der Schnittpunkt der Senkrechten mit dem Thaleskreis bildet mit den Eckpunkten der konstruierten Strecke ein rechtwinkliges Dreieck. Die Höhe der Hypotenuse hat gerade die Länge 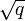$\sqrt{q}$, was aus dem Höhensatz folgt.

Sodann konstruiere man eine Strecke p mit Länge 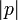$\vert p\vert$ und schlage den Thaleskreis darüber. Anschließend errichte man an den Eckpunkten von p (nach einer Seite hin) Senkrechten, auf denen man zwei Punkte im Abstand 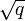$\sqrt{q}$ abtrage. Die Verbindungslinien dieser beiden Punkte bildet eine Sehne durch den Thaleskreis.

Jeder dieser Schnittpunkte hat offenbar den Abstand 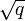$\sqrt{q}$ zu der Seite p. An einem der Schnittpunkte dieser Sehne mit dem Thaleskreis konstruiere man ein Dreieck mit der Seite p. Die Höhe der Seite p teilt diese Seite im Verhältnis $\vert x_1\vert :\vert x_2\vert$.
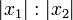Erklärung: Bezeichnet man die so gewonnenen beiden Teile der Seite p als x₁ und x₂, so ist zum einen nach dem Höhensatz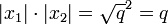 $\vert x_1\vert \cdot \vert x_2\vert = \sqrt{q}^2 = q$ zum anderen gilt 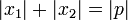$\vert x_1\vert + \vert x_2\vert = \vert p \vert$. Beides trifft aber auch auf die Lösungen des Satzes von Vieta zu und damit sind dies die gesuchten Lösungen.

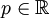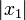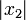Im zweiten Falle seien q < 0 und $p\in \mathbb{R}$. Wir erhalten damit für die quadratische Gleichung eine positive und eine negative Lösung. Um $\vert x_1\vert$ und $\vert x_2 \vert$ wieder als durch die Höhe getrennte Teile der Hypotenuse eines Dreiecks zu erhalten, konstruiere man wie folgt eine Strecke c mit der Länge $\vert x_1 \vert + \vert x_2\vert$.

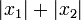Da q < 0 ersetzen wir − q kurzerhand durch $+\vert q\vert$.

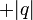Für x₁ ist aber 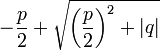$- {p\over 2} + \sqrt{ \left ( {p\over 2}\right )^2 +\vert q\vert }$ stets positiv, da der Wurzelterm offensichtlich stets größer als 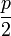${p\over 2}$ ist. Damit ist 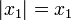$\vert x_1\vert = x_1$. Sicherlich ist x₂ stets negativ und daher ist 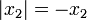$\vert x_2 \vert = -x_2$. Es gilt mithin 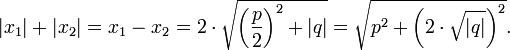$\vert x_1\vert +\vert x_2 \vert = x_1 - x_2 = 2\cdot \sqrt{ \left ({p\over 2} \right )^2 +\vert q\vert} = \sqrt{ p^2+ \left(2\cdot \sqrt{ \vert q\vert}\right )^2 }.$ Letzteres entspricht nach dem Satz des Pythagoras der Länge einer Hypotenuse über zwei Katheten der Länge 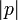$\vert p\vert$ und $2\cdot \sqrt{ \vert q\vert}$.

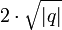Damit ist klar, was zu tun ist. Man konstruiere wieder 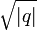$\sqrt{\vert q\vert }$ wie oben beschrieben, trage bei zwei aufeinander senkrecht stehenden Strahlen an einem 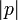$\vert p\vert$ und an dem anderen 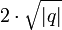$2\cdot \sqrt{\vert q\vert }$ ab und ziehe zwischen den Verbindungslinien eine Strecke. Über dieser Strecke schlage man den Thaleskreis, suche auf diesem einen Punkt mit Abstand 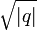$\sqrt{\vert q\vert}$ wie oben beschrieben und konstruiere aus diesem und den Eckpunkten der Strecke ein rechtwinkliges Dreieck. Die Höhe der Strecke teilt die Strecke genau im Verhältnis $\vert x_1\vert :\vert x_2\vert$.

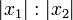Verallgemeinerung (abstrakte Algebra)

Allgemein nennt man eine Gleichung der Form

x² + px + q = 0

mit Elementen p, q eines Körpers oder Rings eine quadratische Gleichung. In einem Körper und bestimmten Ringen (faktorielle Ringe) hat sie höchstens zwei Lösungen, in beliebigen Ringen kann sie mehr als zwei haben. Falls Lösungen in dem betrachteten Ring oder Körper existieren, dann erhält man sie ebenfalls mit der pq-Formel, falls die Charakteristik des Ringes ungleich 2 ist. Hierbei sind allerdings alle möglichen Quadratwurzeln der Diskriminante zu berücksichtigen.

Z.B. hat die quadratische Gleichung

x² - 1 = 0

im Restklassenring 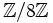$\Z/8\Z$ die vier Lösungen 1, 3, 5, 7.

Geschichte

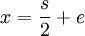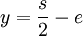Bereits vor 4000 Jahren im Altbabylonischen Reich wurden quadratische Gleichungen gelöst, beispielsweise auf folgende Art: Die quadratische Gleichung x² + p = sx ist äquivalent dem Gleichungssystem xy = p und x + y = s. Für x wird nun der Ansatz $x = \frac{s}{2}+e$ bzw. $y = \frac{s}{2}-e$ gemacht. Für das Produkt p ergibt sich 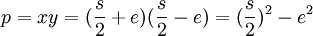$p = xy = (\frac{s}{2}+e)(\frac{s}{2}-e) = (\frac{s}{2})^2 - e^2$. Auflösen der binomischen Formel liefert $e = \sqrt{\frac{1}{4}s^2 - p}$.

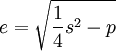Mit e ist damit auch die Lösung x der quadratischen Gleichung bestimmt. Als Beispiel wird die Gleichung x² + 210 = 29x besprochen. Diese ist äquivalent dem Gleichungssystem p = xy = 210 und s = x + y = 29. Der oben genannte Ansatz liefert

$e = \sqrt{\frac{1}{4}s^2 - 210} = \frac{1}{2}.$

Für die Lösung der quadratischen Gleichung ergibt sich $x = \frac{s}{2}+e = \frac{29}{2} + \frac{1}{2} = 15$.

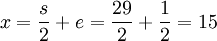Die Griechen kannten keine negative Zahlen und mussten für die quadratische Gleichung mehrere Fallunterscheidungen durchführen. Gleichungen der Art x² + ax = a² werden bei Euklid (II 11) geometrisch gelöst; die Formen ax² + c = bx bzw. ax² + bx = c in Euklid (VI 28) bzw. (VI 29).

geometrische Lösung der Gleichung x² + 10x = 39 nach Euklid

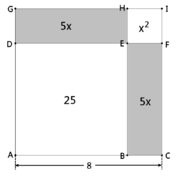
Als Beispiel soll die Gleichung x² + 10x = 39 als Spezialfall von x² + bx = c mit b,c > 0 geometrisch gelöst werden (siehe Bild). Man zerlegt den linearen Term in zwei Rechtecke DEGH bzw. BCFE der Fläche 5x und fügt diese Rechtecke mit dem Quadrat EFIH der Fläche x² zu einem Gnonom BCIGDE der Fläche x² + 10x zusammen. Ergänzt man dieses Gnonom um das Quadrat der Länge 5 zu einem vollständigen Quadrat ACIG, so hält man für die Flächensumme die Gleichung x² + 10x + 25 = 39 + 25. Der Term der rechten Seite liefert das Quadrat der Seite 8. Die quadratische Gleichung wird also »quadratisch ergänzt« zu (x + 5)² = 64 mit der (positiven) Lösung x = 3.

geometrische Lösung der Gleichung x² + px = q nach Brahmagupta

Bei Aryabhata und Brahmagupta wird die Lösung der Gleichung x² + px = q mit Worten beschrieben. Wie man aus dem Bild (links) ersieht, gilt die folgende Zerlegung des Quadrats:

$x^2+4x\frac{p}{4}+4(\frac{p}{4})^2 = q+(\frac{p}{2})^2 = (x+\frac{p}{2})^2.$

Dies liefert sofort die Lösung in heutiger Schreibweise als $x = \sqrt{(\frac{p}{2})^2+q}-\frac{p}{2}$.

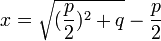Bei Heron von Alexandria und auch bei Al-Chwarizmi wird die Lösung von ax² + bx = c verbal beschrieben; in heutiger Schreibweise als 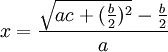$x = \frac{\sqrt{ac+(\frac{b}{2})^2} -\frac{b}{2}}{a}$. Allerdings schiebt Heron den euklidischen Weg als geometrische Begründung nach.

Die allgemeine Lösung in heutiger Schreibweise 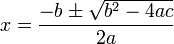$x = \frac{-b \pm \sqrt{b^2-4ac}}{2a}$ entstand erst zu Beginn des 16. Jahrhunderts, als negative Zahlen als Lösung akzeptiert waren und das Wurzelzeichen erfunden war (durch Christoph Rudolff 1525 in seiner Algebra). Einen neuen Ansatz zur Lösung einer quadratischen Gleichung bot der Wurzelsatz von Vieta, der posthum 1615 in seinem Werk De Aequationem Recognitione et Emendatione Tractatus duo publiziert wurde.

Siehe auch

• Lineare Gleichung
• Kubische Gleichung
• Quartische Gleichung

Literatur

• Bartel Leendert van der Waerden: Erwachende Wissenschaft Bd.1 ("Ägyptische, babylonische und griechische Mathematik"), 2.Aufl., Birkhäuser 1966.

Weblinks

• Weblösung zur Lösung quadratischer Gleichungen
• Javascript zur Lösung einer quadratischen Gleichung mit Ausgabe von Normalform, Radikand und Lösungsmenge
• Übungen zu quadratischen Gleichungen mit Korrektur (Javascript)
• Quadratische Gleichung mit komplexen Koeffizienten (Javascript)