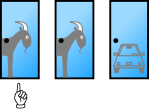
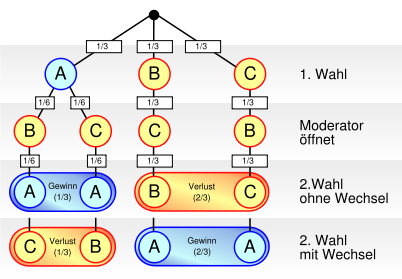
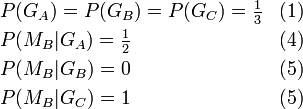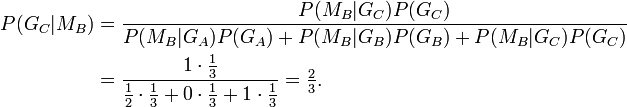Monty-Hall-Dilemma

Auf der Suche nach einem Auto wählt der Kandidat Tor 1. Der Moderator wählt immer ein Tor, hinter dem sich eine Ziege verbirgt (hier Tor 3), öffnet es und schlägt dem Kandidaten vor, das Tor zu wechseln. Ist es vorteilhaft für den Kandidaten, das Tor zu wechseln?

Das Ziegenproblem, Drei-Türen-Problem, Monty-Hall-Problem oder Monty-Hall-Dilemma (nach dem Moderator der US-amerikanischen Spielshow „Let's make a deal“, Monty Hall) ist eine Problemstellung aus der Wahrscheinlichkeitstheorie. Es wird oft als Beispiel dafür herangezogen, dass der menschliche Verstand zu Trugschlüssen neigt, wenn es um das Schätzen von Wahrscheinlichkeiten geht.

Problem und Lösung

Problem

Bei einer Spielshow kann der Kandidat ein Auto gewinnen. Dem Spiel liegen die folgenden Regeln zugrunde.

1. Ein Auto und zwei Ziegen werden zufällig auf drei Tore verteilt.
2. Zu Beginn des Spiels sind alle Tore verschlossen, sodass Auto und Ziegen nicht sichtbar sind.
3. Der Kandidat wählt ein Tor aus, welches aber vorerst verschlossen bleibt.
4. Hat der Kandidat das Tor mit dem Auto gewählt, dann öffnet der Moderator zufällig ausgewählt eines der beiden anderen Tore, hinter dem sich immer eine Ziege befindet.
5. Hat der Kandidat ein Tor mit einer Ziege gewählt, dann öffnet der Moderator dasjenige der beiden anderen Tore, hinter dem die zweite Ziege steht.
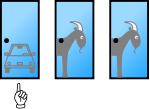
6. Der Moderator bietet dem Kandidaten an, seine Entscheidung zu überdenken und das andere ungeöffnete Tor zu wählen.
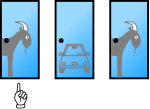
7. Das vom Kandidaten letztlich gewählte Tor wird geöffnet und er erhält das Auto, falls es sich hinter diesem Tor befindet.

Diese Regeln sind dem Kandidaten bekannt. Wie soll er sich im vorletzten Schritt entscheiden, um seine Gewinnchance zu maximieren?

Lösung

Der Kandidat sollte das Tor wechseln. Seine Gewinnwahrscheinlichkeit beträgt dann 2/3.

Erklärung der Lösung

Beweis

Dass die Gewinnwahrscheinlichkeit bei einem Wechsel 2/3 beträgt, wird an dem Beispiel gezeigt, dass der Kandidat zunächst Tür 1 wählt und der Moderator die Ziegentür 3 öffnet. Für die anderen möglichen Kombinationen verläuft der Beweis völlig analog.

Die Wahrscheinlichkeit dafür, dass das Auto hinter Tür 2 steht und der Moderator Tür 3 öffnet, ist doppelt so groß wie die Wahrscheinlichkeit, dass das Auto hinter Tür 1 steht und der Moderator Tür 3 öffnet.

Denn die Wahrscheinlichkeit dafür, dass der Moderator Tür 3 öffnet, wenn das Auto hinter Tür 2 steht, ist nach Spielregel 5 gleich 1, während die Wahrscheinlichkeit dafür, dass er Tür 3 öffnet, wenn das Auto hinter Tür 1 steht, nach Spielregel 4 gleich 1/2 ist.

Da zu Beginn des Spiels nach Spielregel 1 das Auto mit der gleichen Wahrscheinlichkeit 1/3 hinter Tür 1 oder Tür 2 steht, ergibt sich daraus die Ausgangsthese.

Denn die beiden bedingten Wahrscheinlichkeiten 1 und 1/2 müssen jetzt nur noch jeweils mit dem gleichen Faktor 1/3 multipliziert werden, um die Verbundwahrscheinlichkeiten für Tür 2 und Tür 1 bei geöffneter Ziegentür 3 zu erhalten:

1 * (1/3) = 1/3 bzw. (1/2) * (1/3) = 1/6

Für Tür 2 ergibt sich damit die Gewinnwahrscheinlichkeit (1/3) / (1/3 + 1/6) = 2/3, für Tür 1 die Gewinnwahrscheinlichkeit (1/6) / (1/3 + 1/6) = 1/3.

Beweis mit detaillierten Einzelschritten

Im folgenden wird der Fall angenommen, dass der Kandidat zunächst auf Tor 1 zeigt. Die Begründung für die anderen beiden Fälle verläuft völlig analog. Die in Klammern angegebenen Zahlen beziehen sich zur Begründung der jeweiligen Aussage auf die entsprechende Bedingung der oben aufgeführten Aufgabenstellung.

In 1/3 der Fälle steht das Auto hinter Tor 1. (1) In der Hälfte dieser Fälle, also in 1/6 der Gesamtzahl der Fälle, wird vom Moderator Tor 2 geöffnet, in einem weiteren Sechstel Tor 3. (4)

In 2/3 der Fälle steht das Auto hinter Tor 2 oder Tor 3, und zwar in der einen Hälfte dieser Fälle hinter Tor 2, in der anderen Hälfte hinter Tor 3. (1) Entsprechend wird in der einen Hälfte dieser Fälle, also in einem Drittel der Gesamtzahl der Fälle, vom Moderator Tor 2 geöffnet, in der anderen Hälfte Tor 3. (5)

Durch das Öffnen des Nietentors 2 oder 3 reduziert sich die Zahl der Fälle, bei denen das Auto hinter Tor 2 oder 3 steht, um die Hälfte, also auf 1/3 der Gesamtzahl der Fälle.

Außerdem reduziert sich die Zahl der Fälle, bei denen das Auto hinter Tor 1 steht, ebenfalls um die Hälfte, also auf 1/6 der Gesamtzahl der Fälle.

Die Gewinnwahrscheinlichkeit für dasjenige der Tore 2 oder 3, das der Moderator nicht geöffnet hat, beträgt also (1/3)/(1/6 + 1/3) = 2/3.

Das Ergebnis kann man auch so ausdrücken:

Die Gewinnwahrscheinlichkeit für Tor 1 ist eine Invariante des Spiels; ebenso die Gewinnwahrscheinlichkeit für „Tor 2 oder 3“.

Formeller Beweis

Es sind die Ereignisse definiert:

M_A: Der Moderator hat das Tor A geöffnet

G_A: Der Gewinn ist im Tor A

analog für die Indizes B und C

Es liege beispielsweise folgende Situation vor: Der Kandidat hat Tor A gewählt, und der Moderator hat daraufhin das Tor B geöffnet. Lohnt es sich für den Kandidaten zu wechseln? Wie groß ist die Wahrscheinlichkeit, dass das Auto hinter Tor C ist? Gesucht ist also die bedingte Wahrscheinlichkeit P(G_C | M_B), dass das Auto hinter Tor C ist, wenn bekannt ist, dass es nicht hinter Tor B ist. Man kann diese Wahrscheinlichkeit mit dem Bayesschen Theorem ermitteln.

Auf Grund der Aufgabenstellung liegen folgende Voraussetzungen vor:

$\begin{align} &P(G_A) = P(G_B) = P(G_C) = \tfrac{1}{3} &(1) \\ &P(M_B|G_A) = \tfrac{1}{2} &(4)\\ &P(M_B|G_B) = 0 &(5)\\ &P(M_B|G_C) = 1 &(5) \end{align}$

Die Anwendung des Satzes von Bayes ergibt dann Folgendes:

$\begin{align} P(G_C|M_B) & = \frac{P(M_B|G_C)P(G_C)}{P(M_B|G_A)P(G_A)+P(M_B|G_B)P(G_B)+P(M_B|G_C)P(G_C)}\\ & = \frac{ 1 \cdot \tfrac{1}{3} } { \tfrac{1}{2} \cdot \tfrac{1}{3} + 0 \cdot \tfrac{1}{3} + 1 \cdot \tfrac{1}{3}} = \tfrac{2}{3}.\end{align}$

Der Kandidat sollte wechseln.

Begründung über Wertetabelle

Nach Schritt drei der Problemstellung ergeben sich neun mögliche Kombinationen aus erster Wahl des Kandidaten und Position des Autos:

Wahl=1 und Auto=1 
Wahl=1 und Auto=2 *
Wahl=1 und Auto=3 *
Wahl=2 und Auto=1 *
Wahl=2 und Auto=2
Wahl=2 und Auto=3 *
Wahl=3 und Auto=1 *
Wahl=3 und Auto=2 *
Wahl=3 und Auto=3

Mit dem Stern sind die Kombinationen markiert, bei denen Wechseln zum Gewinn des Autos führt. Es sind sechs der neun Möglichkeiten, also führt in sechs von neun oder 2/3 der Fälle Wechseln zum Gewinn des Autos.

Schema für die „Wechselstrategie“

Für die folgende Erklärung wird festgelegt, dass der Kandidat Tor 1 wählt. (Die gleiche Erklärung lässt sich auch für Tor 2 oder Tor 3 durchführen.) Das Auto steht hinter einem der drei Tore. Wählt der Kandidat die Immer-Wechseln-Strategie, dann führt das in den drei Situationen zu folgendem Resultat.

	Der Kandidat wählt Tor 1 und ihm wird entweder die Ziege von Tor 2 oder Tor 3 gezeigt. Durch einen Wechsel verliert er.
	Der Kandidat wählt Tor 1 und ihm wird die Ziege hinter Tor 3 gezeigt. Durch einen Wechsel gewinnt er.
	Der Kandidat wählt Tor 1 und ihm wird die Ziege hinter Tor 2 gezeigt. Durch einen Wechsel gewinnt er.

Fazit: Er gewinnt in zwei von drei Fällen durch einen Wechsel.

Erklärung mit Hilfe eines Entscheidungsbaumes

Entscheidungsbaum zum Ziegenproblem

Beim Schätzen und Berechnen von Wahrscheinlichkeiten ist es wichtig, keine Informationen, die zur Verfügung stehen, zu übersehen: hier ein Entscheidungsbaum für das Problem. Annahme bei diesem Entscheidungsbaum: Das Auto befindet sich hinter dem Tor A.

Eine Million Tore

Das Ziegenproblem lässt sich auch erklären, indem man die Situation überspitzt. Es gibt dann eine Million Tore und hinter genau einem befindet sich das Auto. Nachdem der Kandidat ein Tor gewählt hat, öffnet der Moderator alle anderen Tore bis auf eines. Hier ist es sofort einsichtig, dass der Kandidat wechseln sollte: Die Wahrscheinlichkeit, mit dem zuerst gewählten Tor richtig zu liegen, ist sehr gering. Wenn man die Zahl der Tore verringert, ändert sich nichts daran, dass der Kandidat das Tor wechseln sollte, nachdem der Moderator alle bis auf eine Niete entfernt hat. Insbesondere gilt dies auch für den Fall mit drei Toren.

Sprachlich einfache Erklärungen

Der Moderator kann nur ein Tor öffnen, hinter dem sich der Gewinn nicht befindet. Er muss in der hier besprochenen Aufgabenstellung immer ein Tor wählen. Ein Kandidat, der sich immer gegen den Wechsel entscheidet, gewinnt nur, wenn er auf Anhieb das richtige Tor trifft. Dies geschieht in einem Drittel der Fälle. Ein Kandidat, der immer wechselt, verliert in allen Fällen, in denen er ohne Wechsel gewonnen hätte, also einem Drittel der Fälle, und gewinnt folglich in zwei Dritteln der Fälle.

Alternativen und Erweiterungen

Alternativ kann man sich auch folgende Interpretation des Spieles durch den Kandidaten vorstellen: Der Kandidat wählt in Gedanken zwei Tore aus, sagt aber das dritte an und bittet den Moderator, eine Niete sicher auszuschließen. Danach ist von seinen zwei innerlich gewählten (nicht angesagten) Toren nur dann eins eine Niete, wenn der Gewinn schon vorher hinter dem einzigen nicht ausgewählten Tor (dem angesagten) versteckt war. Die Chance dafür ist ein Drittel. Folglich ist, wenn der Kandidat immer das Angebot zum Wechsel annimmt, die Gewinnchance zwei Drittel. Anders gesagt: Der Kandidat benutzt den Moderator dadurch zur Mitarbeit, dass er vorgibt, sich für das in Gedanken ausgeschlossene Tor zu entscheiden, woraufhin der Moderator die gewünschte Auswahl in den zwei innerlich gewählten Toren vornimmt. Zum übriggebliebenen Tor wird der Kandidat dann offen wechseln, es gehörte ja ohnehin zu seinen beiden Auswahlkandidaten.

Recht einsichtig wird das Ganze auch, wenn man die Situation etwas erweitert. Zur Vereinfachung der Beschreibung sei dabei angenommen, der Kandidat habe sich für Tor 1 entschieden und der Moderator habe Tor 2 geöffnet, d. h. der Kandidat kann sich zwischen Tor 1 und Tor 3 entscheiden. Ohne dass sich irgendetwas an der Wahrscheinlichkeit ändert, den Gewinn zu bekommen, kann man nun auch annehmen, dass der Moderator dem Kandidaten zusätzlich zu dem Gegenstand hinter Tor 3 auch noch die Ziege hinter Tor 2 schenkt. Ebenfalls ändert sich nichts an der Gewinnwahrscheinlichkeit, wenn der Moderator Tor 2 nun wieder schließt. Und es ändert sich auch nichts an der Gewinnwahrscheinlichkeit, wenn der Moderator die Nummern von den Toren 2 und 3 abnimmt, so dass der Kandidat nicht mehr weiß, welches Tor ursprünglich Nummer 2 und welches 3 war (er bekommt ja sowieso beide). Damit wäre das Problem reduziert auf die Aufgabe, entweder Tor 1 zu wählen oder aber die beiden anderen, wobei klar ist, dass hinter einem der anderen beiden Tore eine Ziege steht. Betrachtet man nun diese Aufgabenstellung losgelöst vom ursprünglichen Problem, wird intuitiv jeder zur Wahl der beiden anderen Tore tendieren, denn bei der Wahl von zwei Toren ist logischerweise die Gewinnwahrscheinlichkeit höher als bei der Wahl nur eines Tores.

Leserbrief an Marilyn vos Savant

Ein Leserbrief von Craig F. Whitaker aus Columbia, Maryland an Marilyn vos Savant enthielt die folgende Aufgabenstellung:

„„Nehmen Sie an, Sie wären in einer Spielshow und hätten die Wahl zwischen drei Toren. Hinter einem der Tore ist ein Auto, hinter den anderen sind Ziegen. Sie wählen ein Tor, sagen wir, Tor Nummer 1, und der Showmaster, der weiß, was hinter den Toren ist, öffnet ein anderes Tor, sagen wir, Nummer 3, hinter dem eine Ziege steht. Er fragt Sie nun: 'Möchten Sie das Tor Nummer Zwei?' Ist es von Vorteil, das Tor Nummer 2 zu wählen?“

– Game-Show-Problem^[1]

Gegenüber der Definition des Ziegenproblems in diesem Artikel fehlen unter anderem zwei wesentliche Punkte: die Regeln für den Showmaster sind nicht formuliert und es ist nicht ersichtlich, ob der Kandidat die Regeln kennt. Damit der Kandidat trotzdem mindestens eine 50-prozentige Chance auf den Gewinn hat, muss er zufällig eines der beiden verbleibenden Tore öffnen.^[2] Die Gewinnwahrscheinlichkeit bei Wechsel wäre beispielsweise Null, wenn der Showmaster nur anbietet zu wechseln, wenn hinter der gewählten Tür ein Auto steht. Sie beträgt 50%, wenn er das vom Teilnehmer gewählte Tor öffnet und dahinter eine Ziege ist. Sie ist nicht wohldefiniert, wenn der Showmaster die entsprechenden Strategien willkürlich ändert.

In ihrer ersten Antwort auf den Leserbrief erklärte Marilyn vos Savant die Lösung des Problems ähnlich wie bei „eine Million Tore“ dargestellt.^[1]

Durch die Antwort von Marilyn vos Savant auf den Leserbrief, die richtige – aber unerwartete – Strategie sei „immer wechseln“, wurde das Problem international auch außerhalb der Mathematik in großem Maße bekannt und erzielte große Aufmerksamkeit und Kontroversen.

Ähnliche Aufgaben

Zum Ziegenproblem gibt es mit dem Drei-Kasten-Problem und dem Gefangenenparodoxon zwei Aufgaben, die die gleiche Problematik mit anderen Hintergrundgeschichten erzählen. Daneben gibt es noch die Spielshow „Geh aufs Ganze!“, die zwar Ähnlichkeiten mit dem Ziegenproblem aufweist, aber letztendlich ein anderes Problem darstellt.

Bertrands Schachtelparadoxon

Bei Joseph Bertrands Drei-Kasten-Problem aus dem Jahr 1889 gibt es drei Kästen mit je zwei geschlossenen Schubladen. Im ersten Kasten liegt in jeder Schublade eine Goldmünze. Im zweiten Kasten liegt in jeder Schublade eine Silbermünze und im dritten Kasten liegt in der einen Schublade eine Gold- und in der anderen eine Silbermünze. Jemand wählt zufällig einen Kasten aus und öffnet ebenso zufällig eine der beiden Schubladen. In dieser liegt eine Goldmünze. Mit welcher Wahrscheinlichkeit ist nach dem Öffnen der Schublade in der anderen Schublade eine Silbermünze? Auch hier ist die Antwort $\tfrac 1 3$.

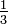Gefangenenparadoxon

→ Hauptartikel: Gefangenenparadoxon

Beim Gefangenenparadoxon aus dem Jahr 1959 spielt die Hintergrundgeschichte in einem Gefängnis. Dort sitzen drei zum Tode verurteilte Gefangene: Anton, Brigitte und Clemens. Genau einer von ihnen soll begnadigt werden. Dazu wird ein Los gezogen, das allen die gleiche Chance gibt, begnadigt zu werden. Der Gefangene Anton bittet den Wärter, der das Ergebnis des Losentscheids kennt, ihm einen seiner Leidensgenossen Brigitte oder Clemens zu nennen, der oder die sterben muss. Der Wärter antwortet ‚Brigitte‘. Wie hoch ist nun Antons Überlebenswahrscheinlichkeit? Auch hier ist die Antwort $\tfrac 1 3$.

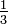Geh aufs Ganze!

→ Hauptartikel: Geh aufs Ganze!

Das Ziegenproblem ähnelt der Spielshow „Geh aufs Ganze!“, unterscheidet sich aber in einem wesentlichen Punkt: Beim Ziegenproblem ist immer genau ein Gewinn vorhanden. Bei „Geh aufs Ganze“ können auch mehrere und wertmäßig unterschiedliche Gewinne vorhanden sein, unter anderem auch ein offenes Geldangebot in bar. Der Moderator bietet dem Spieler Geld, wenn er sich umentscheidet und das vom Moderator gewollte Tor nimmt. Der Moderator feilscht regelrecht mit dem Spieler, erhöht sein Angebot (100, 200, 300… Euro) und geht bis zu einem Limit, das der Spieler vorher nicht kennt. Wenn sich dann der Spieler nicht sofort für das Geld entscheidet, ist das Angebot weg und der Spieler muss das gewählte Tor nehmen. Deshalb unterscheidet sich hier die optimale Strategie. Sie hängt maßgeblich von der Risikoaversion des Kandidaten ab. Der Moderator erhöht schrittweise die sichere Alternative (das Geldangebot), bleibt dabei jedoch unter dem Wert des Hauptpreises. Der Kandidat muss entscheiden, ob ihm das sichere Geldangebot mehr wert ist als die Chance auf den Hauptgewinn. Die Entscheidungstheorie nennt dies das Sicherheitsäquivalent.

Literatur

• Gero von Randow: Das Ziegenproblem – Denken in Wahrscheinlichkeiten. Rowohlt, Reinbek 1992, ISBN 3-499-19337-X, Neuauflage: Rowohlt, Reinbeck 2004, ISBN 3-499-61905-9
• Olle Häggström: Streifzüge durch die Wahrscheinlichkeitstheorie. Springer, Berlin 2005, ISBN 3-540-23050-5
• Henk Tijms: Understanding Probability, Chance Rules in Everyday Life. University Press, Cambridge 2004, ISBN 0521833299
• Gerd Gigerenzer: Das Einmaleins der Skepsis – Über den richtigen Umgang mit Zahlen und Risiken. Berlin-Verlag, Berlin 2002, ISBN 3-8270-0079-3
• Hans-Otto Georgii: Stochastik, Einführung in Wahrscheinlichkeitstheorie und Stochastik, Seite 54 f, Gruyter, August 2004, ISBN 3-11-018282-3
• Norbert Henze:Stochastik für Einsteiger. Vieweg 1997, ISBN 3-528-06894-9, S. 51-52, 105-107
• Grinstead, Charles M. and Snell, J. Laurie: Grinstead and Snell’s Introduction to Probability (PDF), Online version of Introduction to Probability, 2nd edition, American Mathematical Society, Copyright (C) 2003 Charles M. Grinstead and J. Laurie Snell. 2006-07-04(Zugriff am 2. April 2008)

Weblinks

• Recht anschauliche Beschreibung
• Die Zeit: Das Rätsel der drei Türen
• Matheprisma der Uni Wuppertal: Ziegenproblem – Online Simulation, bedingte und totale Wahrscheinlichkeit, Bayes-Formel

Einzelnachweise

1. ↑ ^{a b} Game-Show-Problem – gesammelte Leserbriefe und Antworten innerhalb des Webauftritts von Marilyn vos Savant
2. ↑ Marc Steinbach: Autos, Ziegen und Streithähne. In: Konrad-Zuse-Zentrum für Informationstechnik Berlin (ZIB). Report Nr. 40, S. 7