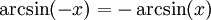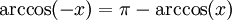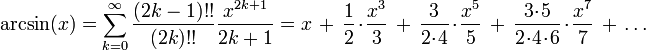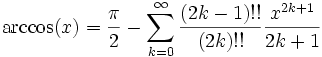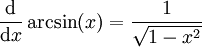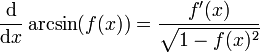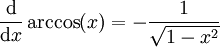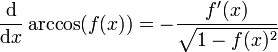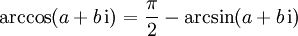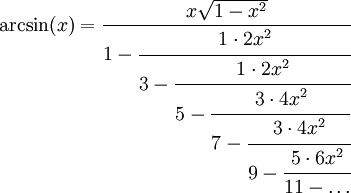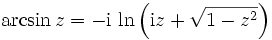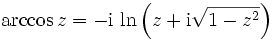- Arkus-Sinus
-
Der Arkussinus (geschrieben arcsin, asin oder sin − 1) ist die Umkehrfunktion der eingeschränkten Sinusfunktion; der Arkuskosinus (geschrieben arccos, acos oder cos − 1) ist die Umkehrfunktion der eingeschränkten Kosinusfunktion. Beide Funktionen gehören damit zur Klasse der Arkusfunktionen. Die Schreibweisen cos − 1 und sin − 1, die immer noch auf einigen Taschenrechnern verwendet werden, sollten vermieden werden, um Verwechslungen mit dem Sekans bzw. Kosekans zu vermeiden.
Inhaltsverzeichnis
Definitionen
Die Sinusfunktion ist 2π-periodisch und innerhalb einer Periode nicht injektiv. Daher muss ihr Definitionsbereich eingeschränkt werden, damit sie umkehrbar-eindeutig wird. Da es für diese Einschränkung mehrere Möglichkeiten gibt, spricht man von Zweigen des Arkussinus. Meist wird der Hauptzweig (oder Hauptwert), die Umkehrfunktion der Einschränkung
![\sin|_{\left[-\frac{\pi}{2},\frac{\pi}{2}\right]}](/pictures/dewiki/57/9a6d93ec693b6051bf2d2b40cfa009d9.png) betrachtet. In diesem Fall entsteht die bijektive Funktion mit
betrachtet. In diesem Fall entsteht die bijektive Funktion mitAnalog zum Arkussinus wird der Hauptwert des Arkuskosinus definiert als die Umkehrfunktion von cos | [0,π]. Diese Definition führt zu der bijektiven Funktion
die sich mittels
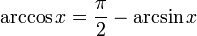 ineinander umrechnen lassen.
ineinander umrechnen lassen.Eigenschaften
Arkussinus Arkuskosinus Funktions-
Graphen
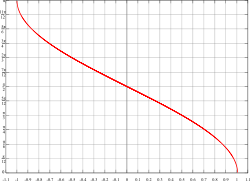
Definitionsbereich 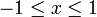
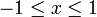
Wertebereich 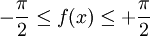
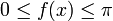
Monotonie streng monoton steigend streng monoton fallend Symmetrien Ungerade Funktion: 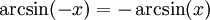
Punktsymmetrie zu 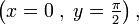
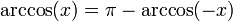
Asymptoten 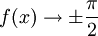 für
für 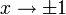
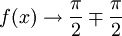 für
für 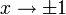
Nullstellen 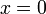
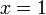
Sprungstellen keine keine Polstellen keine keine Extrema keine keine Wendepunkte 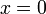
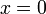
Formeln für negative Argumente
Aufgrund der Symmetrieeigenschaften gilt:
Reihenentwicklungen
Die Taylorreihe des Arkussinus erhält man durch Anwenden der binomischen Reihe auf die Ableitung, sie ist gegeben durch:
Der Ausdruck k!! bezeichnet dabei die Doppelfakultät.
Die Taylorreihe des Arkuskosinus ist aufgrund der Beziehung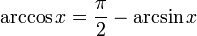 :
:Verkettungen mit Sinus und Kosinus
Für die Arkusfunktionen gelten unter anderem folgende Formeln:
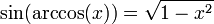 , denn für
, denn für 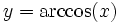 gilt
gilt ![y\in \left[ 0, {\pi} \right]](/pictures/dewiki/55/71f941be562f54aa7b3cd7fb8cfffd3b.png) und
und 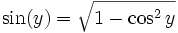 .
.
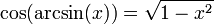 , denn für
, denn für 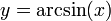 gilt
gilt ![y\in \left[ -\frac{\pi}{2}, \frac{\pi}{2} \right]](/pictures/dewiki/51/30809e2e687acc43c7e0ac768fc00953.png) und
und 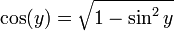 .
.
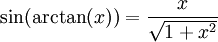 , denn für
, denn für 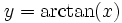 gilt
gilt ![y\in \left]-\frac{\pi}{2}, \frac{\pi}{2}\right[](/pictures/dewiki/97/ad1449c2058e614ff7fb65f03d9222ca.png) und
und 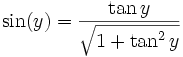 .
.
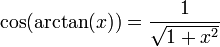 , denn für
, denn für 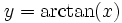 gilt
gilt ![y\in \left]-\frac{\pi}{2}, \frac{\pi}{2}\right[](/pictures/dewiki/97/ad1449c2058e614ff7fb65f03d9222ca.png) und
und 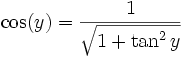 .
.
Ableitungen
- Arkussinus
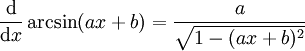
Spezialfall für a = 1 und b = 0:
Allgemein:
- Arkuskosinus
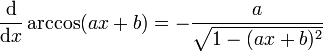
Spezialfall für a = 1 und b = 0:
Allgemein:
- Umrechnung
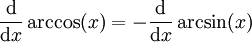
Integrale
- Arkussinus
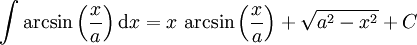
- Arkuskosinus
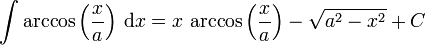
Komplexe Argumente
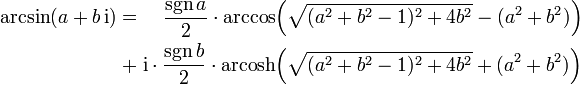 mit
mit 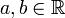
Wobei für die Signumfunktion gilt
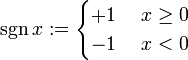
Anmerkungen
Besondere Werte
x − 1 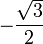
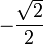
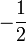
0 
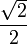
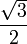
1 arcsin(x) 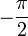
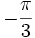
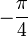
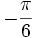
0 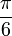
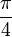
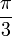
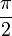
x − 1 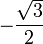
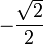
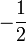
0 
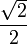
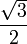
1 arccos(x) π 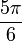
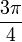
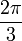
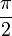
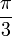
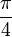
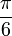
0 Kettenbruchdarstellung des Arkussinus
H. S. Wall fand 1948 folgende Kettenbruchdarstellung für den Arkussinus:
Sonstiges
Man kann Arkussinus und Arkuskosinus auch durch den Hauptzweig des komplexen Logarithmus ausdrücken:
Siehe auch
Literatur
- Ilja Bronstein, Konstantin Semendjajew: Taschenbuch der Mathematik. B.G. Teubner, Stuttgart 1991. ISBN 3-87144-492-8
Primäre trigonometrische Funktionen
Sinus und Kosinus | Tangens und Kotangens | Sekans und KosekansUmkehrfunktionen (Arkusfunktionen)
Arkussinus und Arkuskosinus | Arkustangens und Arkuskotangens | Arkussekans und ArkuskosekansHyperbelfunktionen
Sinus Hyperbolicus und Kosinus Hyperbolicus | Tangens Hyperbolicus und Kotangens Hyperbolicus | Sekans Hyperbolicus und Kosekans HyperbolicusAreafunktionen
Areasinus Hyperbolicus und Areakosinus Hyperbolicus | Areatangens Hyperbolicus und Areakotangens Hyperbolicus | Areasekans Hyperbolicus und Areakosekans Hyperbolicus
Wikimedia Foundation.

![\arcsin\colon[-1,1]\to \left[-\frac{\pi}{2},\frac{\pi}{2} \right].](/pictures/dewiki/102/f5e85f79ad2fa46f52452a5cc61c5c89.png)
![\arccos\colon[-1,1]\to[0,\pi],](/pictures/dewiki/56/8505de47c85fec7e0c74efc75e9632ba.png)