- Differenzoperator
-
Die diskrete Differentialrechnung ist eine Form der Differentialrechnung, die nicht wie in der Analysis mit kontinuierlichen, sondern mit diskreten Mengen arbeitet und zur Berechnung von Reihen angewandt werden kann.
Inhaltsverzeichnis
Differenzen und Summen
Die bekannte kontinuierliche Differentialrechnung basiert auf dem Differenzialoperator D, der wie folgt definiert ist:
Die diskrete Differentialrechnung hingegen verwendet einen sogenannten Differenzoperator Δ:
- Δf(x) = f(x + 1) − f(x).
Die umgekehrte Operation wird nicht wie in der kontinuierlichen Differentialrechnung mit dem unbestimmten Integral, sondern mit einer unbestimmten Summe
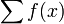 erreicht, die sich zum Differenzoperator wie folgt verhält:
erreicht, die sich zum Differenzoperator wie folgt verhält: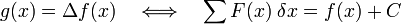 .
.
δ verhält sich hier zu Δ wie d zu D in der kontinuierlichen Differentialrechnung. C steht für den Wert einer beliebigen Funktion, die für ganzzahlige x konstant ist (C(x + 1) = C(x)).
Das Pendant zu bestimmten Integralen sind bestimmte Summen. Diese entsprechen gewöhnlichen Summen ohne den Wert am höchsten Index:
![\sideset{}{_a^b} \sum f(x)\; \delta x = \sum_{k=a}^{b-1} F(k) = [F(x)]_a^b = F(b) - F(a)](/pictures/dewiki/56/87d0587e05ca0fb85c068829f42f7dc7.png) .
.
Eigenschaften
Invariante Funktion
Die unter dem Differenzialoperator invariante Funktion ist die Exponentialfunktion der Basis e. In der diskreten Differentialrechnung ist die Exponentialfunktion der Basis 2 invariant, wie sich leicht ermitteln lässt:
Fallende Fakultäten
Eine einfache Rechenregel gibt es für fallende Fakultäten, die für jede Ganzzahl m wie folgt definiert sind:
Dieser Ausdruck verhält sich in der diskreten Differentialrechnung folgendermaßen:
wobei Hn die n-te harmonische Zahl ist. Die harmonische Reihe ist somit das Gegenstück zum natürlichen Logarithmus.
Fallende Fakultäten können stets mittels Stirling-Zahlen erster Art in Potenzen umgewandelt werden:
![x^{\underline{m}} = \sum_k\left[\begin{matrix} m \\ k \end{matrix}\right] (-1)^{m-k}x^k](/pictures/dewiki/55/79501d366d9fb9d0ddd1426c157690d8.png) .
.
Außerdem gilt der binomische Lehrsatz auch für fallende Fakultäten.
Beispiel zur Berechnung der Summe der ersten n Quadratzahlen:
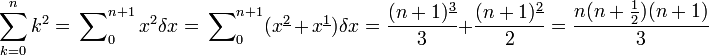 .
.
Produktregel und partielle Summation
Die Produktregel der kontinuierlichen Differentialrechnung ist in folgender Form gültig:
- Δ(u(x)v(x)) = u(x)Δv(x) + v(x + 1)Δu(x).
Diese Regel lässt sich durch Einführung eines Verschiebeoperators E, definiert als Ef(x) = f(x + 1), kompakter ausdrücken:
- Δ(uv) = uΔv + EvΔu.
Die Umstellung der Terme führt zur Formel der partiellen Summation ähnlich der partiellen Integration:
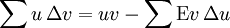 .
.
Beispiel zur Berechnung der Summe
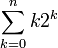 :
:Hier ist u(x) = x und Δv(x) = 2x, sodass Δu(x) = 1, v(x) = 2x und Ev(x) = 2x + 1.
Die Formel zur partiellen Summation ergibt:
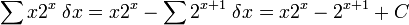 .
.Dies führt schließlich zur Lösung:
Literatur
- Ronald Graham u. a.: Concrete Mathematics. Addison-Wesley, Upper Saddle River 2008, ISBN 0-201-55802-5
Weblinks
- Brian Hamrick: Discrete Calculus (PDF, 70 KB)
Wikimedia Foundation.

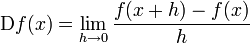
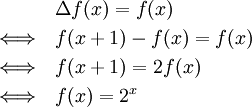

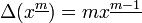
![\sideset{}{_a^b} \sum x^{\underline{m}}\; \delta x =
\begin{cases}
\left[\frac{x^{\underline{m+1}}}{m+1}\right]_a^b & \text{, wenn } m \neq -1 \\
\left[ H_m\right]_a^b & \text{, wenn } m = -1
\end{cases}](/pictures/dewiki/53/59889db58d58df8aa705c00725f45800.png)
![\begin{align}
\sum_{k=0}^n k2^k & = \sideset{}{_0^{n+1}} \sum x2^x\; \delta x \\
& = \left[ x2^x - 2^{x+1} \right ]_0^{n+1} \\
& = (n-1)2^{n+1} + 2
\end{align}](/pictures/dewiki/57/9684f3ffa81bfc87ae3058bcdf47ce94.png)