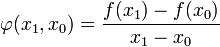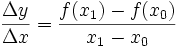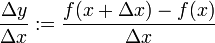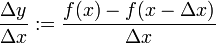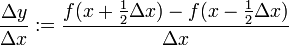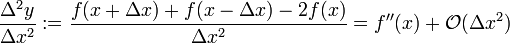- Differenzquotient
-
Der Differenzenquotient ist ein Begriff aus der Mathematik. Er beschreibt das Verhältnis der Veränderung einer Größe zu der Veränderung einer anderen, von der die erste abhängt. In der Analysis verwendet man Differenzenquotienten, um die Ableitung einer Funktion zu definieren. In der numerischen Mathematik werden sie zum Lösen von Differentialgleichungen und für die näherungsweise Bestimmung der Ableitung einer Funktion benutzt.
Inhaltsverzeichnis
Definition
Ist f eine Funktion und
![[x_0;x_1] \subset D_f](/pictures/dewiki/57/9aa8c64aabafac6e9b84ee4a2b757b63.png) , so nennt man den Quotienten
, so nennt man den QuotientenDifferenzenquotient von f im Intervall [x0;x1].
Häufig setzt man
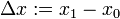 und
und 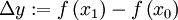 . Damit ergibt sich die alternative Schreibweise
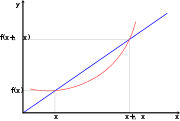
. Damit ergibt sich die alternative SchreibweiseGeometrisch entspricht der Differenzenquotient der Steigung der Sekante des Graphen von f durch die Punkte (x0,f(x0)) und (x0 + Δx,f(x0 + Δx)).
Differentialrechnung
Differenzenquotienten bilden zusammen mit dem Grenzwertbegriff die theoretische Grundlage der Differentialrechnung. Den Grenzwert des Differenzenquotientens für
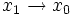 bezeichnet man als Differentialquotienten oder Ableitung der Funktion an der Stelle x0 (kurz: f'(x0)), sofern dieser Grenzwert existiert. Das Berechnen dieses Grenzwerts nennt man Ableiten oder Differenzieren. Die Tabelle zeigt die Ableitungen einiger Funktionen:
bezeichnet man als Differentialquotienten oder Ableitung der Funktion an der Stelle x0 (kurz: f'(x0)), sofern dieser Grenzwert existiert. Das Berechnen dieses Grenzwerts nennt man Ableiten oder Differenzieren. Die Tabelle zeigt die Ableitungen einiger Funktionen:Funktion 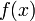
Differenzenquotient 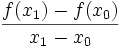
Differentialquotient 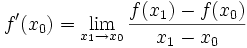
Umformung Konstante Funktion 
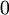
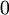
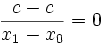
(Homogene) Lineare Funktion 
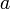
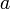
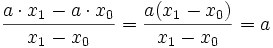
Quadratfunktion 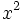
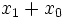
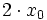
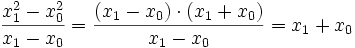
Kubikfunktion 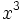
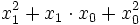
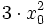
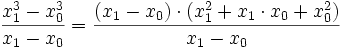
Numerische Mathematik
Bei differenzierbaren Funktionen kann der Differenzenquotient als Näherung für die lokale Ableitung benutzt werden. In der Finite-Differenzen-Methode wird diese Eigenschaft zur Lösung von Differentialgleichungen benutzt. Ebenso wird dies für die numerische Differentiation von Funktionen verwendet.
Dabei ist der Differenzenquotient nicht auf die erste Ableitung beschränkt. Es existieren Differenzenquotienten für höhere sowie partielle Ableitungen.
Beispiel
Es sei
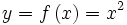 .
.Der Graph von f ist eine Normalparabel. Wollen wir die Ableitung z.B. in der Nähe der Stelle x = 12 ungefähr berechnen, so wählen wir für Δx einen kleinen Wert, z.B. 0,001. Das ergibt als Differenzenquotienten im Intervall [12;12,001] den Wert
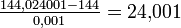 . Dieser ist die Sekantensteigung des Funktionsgraphen im Intervall [12;12,001] und eine Näherung der Steigung der Tangente an der Stelle 12.
. Dieser ist die Sekantensteigung des Funktionsgraphen im Intervall [12;12,001] und eine Näherung der Steigung der Tangente an der Stelle 12.Varianten
In der Praxis werden verschiedene Varianten des Differenzenquotienten verwendet, die sich in der Definition von Δy, etwa um die Genauigkeit bei der Bestimmung des lokalen Wachstums, z.B. der Sekantensteigung eines Graphen, zu verbessern oder um an den Randstellen einer Funktion deren Sekantensteigung „rückwärts“ in Richtung des Inneren ihres Definitionsbereichs zu ermitteln.
Vorwärtsdifferenzenquotient
Der oben definierte Ausdruck
wird auch Vorwärtsdifferenzenquotienten genannt, weil zur Bestimmung des zweiten Funktionswertes, der zur Bildung von Δy notwendig ist, von x aus nach rechts, also „vorwärts“ gegangen wird.
Rückwärtsdifferenzenquotient
Analog bezeichnet man den Ausdruck
als Rückwärtsdifferenzenquotienten, da zur Differenzbildung von x aus nach links, also „rückwärts“ gegangen wird, um den zweiten Funktionswert zu erhalten.
Zentraler Differenzenquotient
Gebräuchlich ist auch der zentralen Differenzenquotient, der durch
gegeben ist. Bei ihm liegen die zur Differenzbildung verwendeten Stellen symmetrisch um den x-Wert, für den die Ableitung angenähert werden soll.
Im Gegensatz zu den beiden vorherigen Differenzenquotienten, deren Fehlerterme beim Annähern der ersten Ableitung an der Stelle x nur von der Klasse
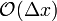 sind, liegt der Fehler des zentrale Differenzenquotienten in
sind, liegt der Fehler des zentrale Differenzenquotienten in 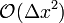 . Dies gilt natürlich nur für Funktionen, die in x differenzierbar sind. Zur
. Dies gilt natürlich nur für Funktionen, die in x differenzierbar sind. Zur 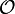 -Notation siehe Landau-Symbole.
-Notation siehe Landau-Symbole.Höhere Differenzenquotienten
Ebenso wie die erste Ableitung durch Differenzenquotienten angenähert werden kann, gilt dies auch für höhere Ableitungen, die über Differenzenquotienten höherer Ordnung approximierbar sind.
Für die zweite Ableitung kann zum Beispiel der Zusammenhang
verwendet werden, zweimalige Differenzierbarkeit der Funktion vorausgesetzt. Die
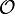 -Konstante ist dabei abhängig von x.
-Konstante ist dabei abhängig von x.
Wikimedia Foundation.