Dirichletsche Beta-Funktion
- Dirichletsche Beta-Funktion
-
Die dirichletsche Beta-Funktion, geschrieben β(s), ist eine spezielle Funktion; sie ist verwandt mit der riemannschen Zeta-Funktion.
Benannt wurde sie nach dem deutschen Mathematiker Peter Gustav Lejeune Dirichlet (1805−1859).
Definitionen
Die dirichletsche β-Funktion ist folgendermaßen definiert:
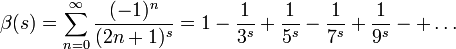
Eine äquivalente Definition ist
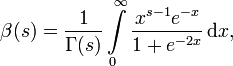
wobei Γ die Gammafunktion bezeichnet.
In beiden Fällen wird Re(s) > 0 vorausgesetzt.
Eine Definitionsmöglichkeit unter Verwendung der hurwitzschen Zetafunktion, die β für alle komplexen s definiert, lautet:
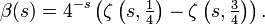
Eine andere gleichwertige Definition für alle komplexen s schließt die transzendente lerchsche Zeta-Funktion Φ ein und lautet
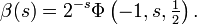
Die analytische Fortsetzung auf die ganze komplexe Zahlenebene ist gegeben durch
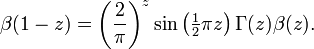
Spezielle Werte
Einige spezielle Werte der β-Funktion sind
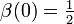
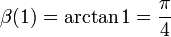
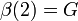
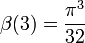
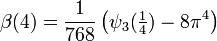
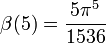
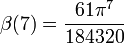
Hierbei bezeichnet G die catalansche Konstante und ψ3(z) ist die Trigamma-Funktion, also die dritte Polygamma-Funktion.
Allgemein gilt für positive ganze Zahlen k die Rekursion
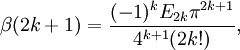
wobei En die n-te Euler-Zahl ist. Im Fall k > 0 vereinfacht sich dies zu
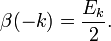
Ferner gilt für natürliche k
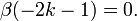
Ableitung
Es gilt
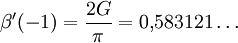
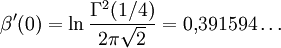
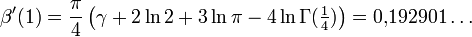
(vgl. Folgen A113847 und A078127 in OEIS)
Außerdem gilt für positive ganze n:
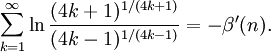
Weiteres
Rivoal and Zudilin bewiesen 2003[1], dass mindestens einer der Werte β(2), β(4), β(6), β(8), β(10) und β(12) irrational ist.
Außerdem bewiesen Guillera und Sandow 2005[2] folgende Formel:
![\int\limits_0^1 \int\limits_0^1 \frac{[-\ln(xy)]^s}{1+x^2y^2}\mathrm dx\mathrm dy =\Gamma(s+2)\beta(s+2)](/pictures/dewiki/57/9886602ad7a466243ccd4ede54d2acb3.png)
Referenzen
- ↑ Tanguy Rivoal, Wadim Zudilin: Diophantine properties of numbers related to Catalan's constant. In: Math. Ann. Band 326, Nummer 4, 2003, Seiten 705-721; vgl. PDF des mathematischen Instituts der Universität Köln
- ↑ Jesús Guillera, Jonathan Sondow: Double integrals and infinite products for some classical constants via analytic continuations of Lerch's transcendent. In: Ramanujan J. Band 16, Nummer 3, 2008, Seiten 247-270; vgl. in arxiv
Weblinks
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
Beta-Funktion — Betafunktion bezeichnet in der Mathematik: Eulersche Betafunktion Β(x), auch Eulersches Integral erster Art Dirichletsche Betafunktion β(s), die mit der riemannschen Zetafunktion verwandt ist … Deutsch Wikipedia
Eulersche Beta-Funktion — Betafunktion bezeichnet in der Mathematik: Eulersche Betafunktion Β(x), auch Eulersches Integral erster Art Dirichletsche Betafunktion β(s), die mit der riemannschen Zetafunktion verwandt ist … Deutsch Wikipedia
Dirichletsche Betafunktion — Die dirichletsche Beta Funktion, geschrieben β(s), ist eine spezielle Funktion; sie ist verwandt mit der riemannschen Zeta Funktion. Benannt wurde sie nach dem deutschen Mathematiker Peter Gustav Lejeune Dirichlet (1805−1859). Inhaltsverzeichnis… … Deutsch Wikipedia
Spezielle Funktion — In der Analysis, einem Teilgebiet der Mathematik, bezeichnet man gewisse Funktionen als spezielle Funktionen, weil sie sowohl in der Mathematik selbst als auch in ihren Anwendungen (z. B. in der mathematischen Physik) eine tragende Rolle… … Deutsch Wikipedia
Lerchsche Zeta-Funktion — Die Lerchsche Zeta Funktion (nach Mathias Lerch) ist eine sehr allgemeine Zeta Funktion. Sehr viele Reihen reziproker Potenzen (einschließlich der hurwitzschen Zeta Funktion und des Polylogarithmus) können als Spezialfall dieser Funktion… … Deutsch Wikipedia
Legendresche Chi-Funktion — Die Legendresche χ Funktion (Chi Funktion) ist in der Mathematik eine spezielle Funktion, die folgendermaßen definiert ist: Sie lässt sich auch mit dem Polylogarithmus Liν(z) ausdrücken: Inhaltsverzeichnis … Deutsch Wikipedia
Zeta-Funktion — Ursprünglich war mit Zeta Funktion oder ζ Funktion in der Mathematik die komplexe Funktion gemeint. Heute heißt diese genauer Riemannsche Zeta Funktion, zu Ehren von Bernhard Riemann, der um 1850 bedeutende Arbeiten zur Untersuchung dieser… … Deutsch Wikipedia
Clausen-Funktion — In der Mathematik ist die Clausen Funktion durch das folgende Integral definiert: Inhaltsverzeichnis 1 Allgemeine Definition 2 Beziehung zum Polylogarithmus … Deutsch Wikipedia
Höhere transzendente Funktionen — Das Gebiet der speziellen Funktionen beschäftigt sich mit gewissen Funktionen, die sowohl in der Mathematik selbst als auch in den angewandten Wissenschaften (z. B. mathematische Physik) häufig auftreten. Die meisten Funktionen von Interesse sind … Deutsch Wikipedia
Spezielle Funktionen — Das Gebiet der speziellen Funktionen beschäftigt sich mit gewissen Funktionen, die sowohl in der Mathematik selbst als auch in den angewandten Wissenschaften (z. B. mathematische Physik) häufig auftreten. Die meisten Funktionen von Interesse sind … Deutsch Wikipedia

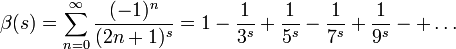
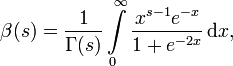
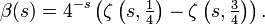
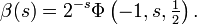
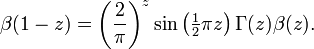
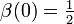
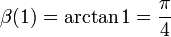
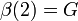
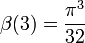
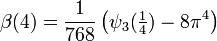
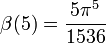
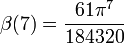
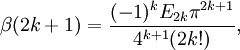
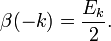
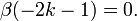
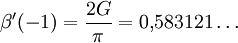
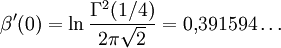
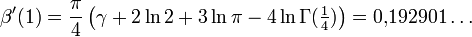
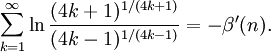
![\int\limits_0^1 \int\limits_0^1 \frac{[-\ln(xy)]^s}{1+x^2y^2}\mathrm dx\mathrm dy =\Gamma(s+2)\beta(s+2)](/pictures/dewiki/57/9886602ad7a466243ccd4ede54d2acb3.png)