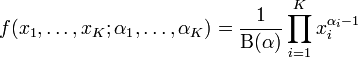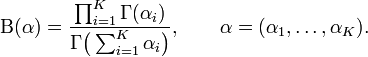Dirichletverteilung

Beispiele einer Dirichlet-Verteilung mit K=3 für verschiedene Parametervektoren α. Im Uhrzeigersinn von oben links: α=(6, 2, 2), (3, 7, 5), (6, 2, 6), (2, 3, 4).

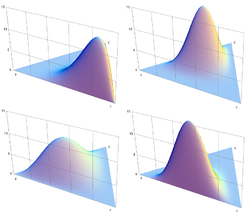
Die Dirichletverteilung (nach Peter Gustav Lejeune Dirichlet) ist eine Familie von stetigen, multivariaten Wahrscheinlichkeitsverteilungen.

Sie ist die multivariate Erweiterung der Beta-Verteilung und die a-priori-Verteilung der multinomialen Verteilung in Bayesscher Statistik. Ihre Dichtefunktion gibt die Wahrscheinlichkeiten von K verschiedenen, exklusiven Ereignissen an, wenn jedes Ereignis α_i − 1 mal beobachtet wurde.

Veranschaulichung

Die multinomiale Verteilung gibt die Wahrscheinlichkeiten p_k für k unterschiedliche Ereignisse an, also z.B. wie wahrscheinlich es ist eine Sechs zu würfeln. Im Gegensatz dazu gibt die Dirichlet-Verteilung an, wie wahrscheinlich eine Verteilung ist, könnte also im Falle einer Würfelfabrik angeben, wie wahrscheinlich die Verteilungen der Würfelergebnisse bei den fabrizierten Würfeln sind. Im Falle von exakten Maschinen wäre diese bei allem anderen als der uniformen Verteilung (alle Augenzahlen gleichwahrscheinlich) sehr gering, was einem α mit gleichen und sehr hohen Elementen wie etwa (1000,1000,1000,1000,1000,1000) entspräche. α = (1000,500,500,500,500,500) würde bedeuten, dass die Maschinen Würfel fabrizieren, bei denen die Augenzahl 1 doppelt so häufig vorkommt wie jede andere Augenzahl. Und dies fast ausnahmslos, da die Werte wiederum sehr hoch sind und damit die Varianz niedrig. Wären die Werte in α alle 0,1 bedeutete dies, dass Würfel hergestellt werden die eine starke Tendenz zu einer Augenzahl haben. Jedoch ist diese bevorzugte Augenzahl eines Würfels zufällig und ohne Tendenz zu bestimmten Bevorzugungen, da alle Werte in α gleich sind. Je kleiner die Werte, desto seltener sind Würfel, die nicht nur eine Augenzahl ergeben.

Dichtefunktion

Die Dirichletverteilung der Ordnung K ≥ 2 mit den Parametern α₁,...,α_K > 0 hat folgende Dichtefunktion:

$f(x_1,\dots, x_{K}; \alpha_1,\dots, \alpha_K) = \frac{1}{\mathrm{B}(\alpha)} \prod_{i=1}^K x_i^{\alpha_i - 1}$

für alle x₁,...,x_{K − 1} > = 0 mit x₁ + ... + x_{K − 1} < = 1 und x_K = 1 − (x₁ + ... + x_{K − 1}). Daher ist die Summe aller Wahrscheinlichkeiten x_i,i = 1...K gleich 1.

Die normierende Konstante ist die multinomiale Betafunktion, welche durch Gammafunktionen dargestellt werden kann:

$\mathrm{B}(\alpha) = \frac{\prod_{i=1}^K \Gamma(\alpha_i)}{\Gamma\bigl(\sum_{i=1}^K \alpha_i\bigr)},\qquad\alpha=(\alpha_1,\dots,\alpha_K).$

Weblinks

• Eintrag in der Encylopedia of Mathematics (Springer)
• Skript, S. 37 (PDF)
• Multivariate Verteilungen (Skript), S. 9 (PDF)

Diskrete univariate Verteilungen

Diskrete univariate Verteilungen für endliche Mengen:
Benford | Bernoulli-Verteilung | Binomialverteilung | Kategoriale | Hypergeometrische Verteilung | Rademacher | Zipfsche | Zipf-Mandelbrot

Diskrete univariate Verteilungen für unendliche Mengen:
Boltzmann | Conway-Maxwell-Poisson | Negative Binomialverteilung | Erweiterte negative Binomial | Compound Poisson | Diskret uniform | Discrete phase-type | Gauss-Kuzmin | Geometrische | Logarithmische | Parabolisch-fraktale | Poisson | Skellam | Yule-Simon | Zeta

 

Kontinuierliche univariate Verteilungen

Kontinuierliche univariate Verteilungen mit kompaktem Intervall:
Beta | Kumaraswamy | Raised Cosine | Dreiecks | U-quadratisch | Stetige Gleichverteilung | Wigner-Halbkreis

Kontinuierliche univariate Verteilungen mit halboffenem Intervall:
Beta prime | Bose-Einstein | Burr | Chi-Quadrat | Coxian | Erlang | Exponential | F | Fermi-Dirac | Folded Normal | Fréchet | Gamma | Extremwert | Verallgemeinerte inverse Gausssche | Halblogistische | Halbnormale | Hotellings T-Quadrat | hyper-exponentiale | hypoexponential | Inverse Chi-Quadrat | Scale Inverse Chi-Quadrat | Inverse Normal | Inverse Gamma | Lévy | Log-normal | Log-logistische | Maxwell-Boltzmann | Maxwell speed | Nakagami | nichtzentrierte Chi-Quadrat | Pareto | Phase-type | Rayleigh | relativistische Breit-Wigner | Rice | Rosin-Rammler | Shifted Gompertz | Truncated Normal | Type-2-Gumbel | Weibull | Wilks’ lambda

Kontinuierliche univariate Verteilungen mit unbeschränktem Intervall:
Cauchy | Extremwert | Exponential Power | Fisher’s z | Fisher-Tippett (Gumbel) | Generalized Hyperbolic | Hyperbolic Secant | Landau | Laplace | Alpha stabile | logistisch | Normal (Gauss) | Normal-inverse Gausssche | Skew normal | Studentsche t | Type-1 Gumbel | Variance-Gamma | Voigt

 

Multivariate Verteilungen

Diskrete multivariate Verteilungen:
Ewen's | Multinomial | Dirichlet Multinomial

Kontinuierliche multivariate Verteilungen:
Dirichlet | Generalized Dirichlet | Multivariate Normal | Multivariate Student | Normalskalierte inverse Gamma | Normal-Gamma

Multivariate Matrixverteilungen:
Inverse-Wishart | Matrix Normal | Wishart