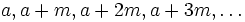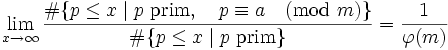Dirichletsches Theorem

Der dirichletsche Primzahlsatz (nach P. G. L. Dirichlet) ist eine Aussage aus dem mathematischen Teilgebiet der Zahlentheorie, der besagt, dass eine arithmetische Folge unendlich viele Primzahlen enthält, wenn dies nicht aus trivialen Gründen unmöglich ist.

In der einfachsten Fassung lautet der Satz: Es sei m eine natürliche Zahl und a eine zu m teilerfremde natürliche Zahl. Dann enthält die arithmetische Folge

$a, a+m, a+2m, a+3m,\ldots$

unendlich viele Primzahlen. Anders formuliert: Es gibt unendlich viele Primzahlen, die kongruent zu a modulo m sind.

Wären a und m nicht teilerfremd und g > 1 ein gemeinsamer Teiler, so wäre jedes Folgenglied durch g teilbar; zwei verschiedene Primzahlen können aber nicht beide durch g teilbar sein. Deshalb ist die Bedingung der Teilerfremdheit von a und m notwendig.

Jede ungerade Zahl hat die Form 4k + 1 oder 4k + 3 mit einer nichtnegativen ganzen Zahl k. Der dirichletsche Primzahlsatz sagt in diesem Spezialfall aus, dass es von beiden Formen jeweils unendlich viele Primzahlen gibt.

In einer quantitativen Fassung, die beispielsweise aus dem tschebotarjowschen Dichtigkeitssatz folgt, lautet der dirichletsche Primzahlsatz:

$\lim_{x\to\infty}\frac{\#\{p\leq x\mid p\ \mathrm{prim},\quad p\equiv a\pmod m\}}{\#\{p\leq x\mid p\ \mathrm{prim}\}}=\frac1{\varphi(m)}$

mit der eulerschen φ-Funktion. Diese Aussage bedeutet, dass es in jeder der primen Restklassen modulo m in einem gewissen Sinne gleich viele Primzahlen gibt.