- Naturton
-
Die Naturtonreihe ist eine stufige Tonfolge, die erklingt, wenn ein schwingendes Medium (beispielsweise: Luftsäule bei Aerophonen, Saite bei Chordophonen) entlang der Schwingungsknoten in aufsteigender Reihenfolge unterteilt wird. Das Phänomen der Naturtonreihe ist physikalisch bedingt und die Intervalle zwischen den Tönen der Reihe sind dadurch fest vorgegeben.
Ein Naturton enthält als seine tiefste Frequenz einen höheren (d. h. nicht den ersten) Teilton des jeweiligen Mediums.
Redundanz und Hierarchie (z. B. die Dominanz des Grundtones bzw. seiner Oktaven sowie Quinte) liegen in der Natur des Tones selbst: Jeder natürliche Ton ist ein aus Teiltönen (Partialtönen, Obertönen, Naturtönen) zusammengesetzter Klang.
Inhaltsverzeichnis
Frequenzbeziehungen
 Die spielbare Tonreihe einer Naturtrompete in C (ca.240 cm lang): Die Zahlen in der oberen Zeile sind die Nummerierung der Naturtöne. Die Zahlen und Pfeile in der unteren Reihe geben die theoretische Abweichung des jeweiligen Naturtones von der „gleichstufig temperierten Stimmung“ in Cent an. Zum Anhören (MIDI)
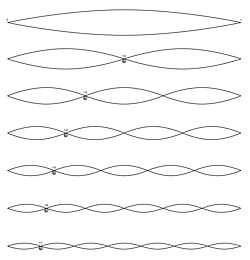
Die spielbare Tonreihe einer Naturtrompete in C (ca.240 cm lang): Die Zahlen in der oberen Zeile sind die Nummerierung der Naturtöne. Die Zahlen und Pfeile in der unteren Reihe geben die theoretische Abweichung des jeweiligen Naturtones von der „gleichstufig temperierten Stimmung“ in Cent an. Zum Anhören (MIDI) Skizzierte Stehende Welle des (von oben nach unten) 1.; 2.; 3.; 4. und 5. Naturtons in einem konischen Blechblasinstrument
Skizzierte Stehende Welle des (von oben nach unten) 1.; 2.; 3.; 4. und 5. Naturtons in einem konischen BlechblasinstrumentDie Frequenzen der in einer gegebenen Luftsäule erzeugbaren stehenden Wellen sind ganzzahlige Vielfache der tiefsten möglichen Frequenz (Grundfrequenz), die somit gleichzeitig der 1. Naturton ist.
Das musikalische Intervall einer Oktave entspricht einer Verdopplung der Frequenz. Somit liegen folgende Töne der Naturtonreihe (innerhalb der ersten 16 Naturtöne) jeweils im Oktavabstand zueinander:
- 1., 2., 4., 8., 16.
- 3., 6., 12.
- 5., 10.
- 7., 14.
Beispiel: Die folgende Tabelle gibt über dem Grundton von 65 Hz (ca. entsprechend dem nebenstehenden Notenbeispiel) die darauf folgenden Naturtöne bis zum 16. Naturton an.
Naturton
Ton
Frequenz
Frequenzverhältnis zum Grundton Harmonischer Abstand zum Grundton Bezeichnung im Orgelbau 1. Naturton (Grundton) C 65 Hz 1:1 Prime verschiedene (Äquallage) 2. Naturton c0 130 Hz 2:1 Oktave Oktave 3. Naturton g0 195 Hz 3:1 Oktave + reine Quinte (Duodezime) Quinte 4. Naturton c1 260 Hz 4:1 2 Oktaven Superoktave, Oktave 5. Naturton e1 325 Hz 5:1 2 Oktaven + große Terz Terz 6. Naturton g1 390 Hz 6:1 2 Oktaven + reine Quinte Superquinte, Quinte 7. Naturton b1 455 Hz 7:1 2 Oktaven + Naturseptime Septime, Sept 8. Naturton c2 520 Hz 8:1 3 Oktaven Oktävlein, Superoktave, Oktave 9. Naturton d2 585 Hz 9:1 3 Oktaven + große Sekunde None 10. Naturton e2 650 Hz 10:1 3 Oktaven + große Terz Terz 11. Naturton fis2 715 Hz 11:1 3 Oktaven + Tritonus Undezime, Elfte 12. Naturton g2 780 Hz 12:1 3 Oktaven + reine Quinte Superquinte, Quinte 13. Naturton gis2 845 Hz 13:1 3 Oktaven + kleine Sexte Tredezime 14. Naturton b2 910 Hz 14:1 3 Oktaven + Naturseptime Septime, Sept 15. Naturton h2 975 Hz 15:1 3 Oktaven + große Septime Durseptime 16. Naturton c3 1040 Hz 16:1 4 Oktaven Superoktave, Oktave Musizierpraxis
Blechblasinstrumente
Der 1. Naturton ist nur in wenigen Fällen sauber intonierend verwendbar (Flügelhorn, Kuhlohorn, manche Trompete), bei dem Naturhorn in F wird bis zum 24. Naturton beblasen.
Die im obenstehenden Notenbeispiel angegebenen Tonhöhendifferenzen in Cent bezogen auf die Gleichstufige Stimmung haben in der Musizierpraxis der Blechblasinstrumente
- mit Ventilen nur relativ geringe Bedeutung, da durch die Verwendung der Ventile und anderer mechanischer Vorrichtungen wie Intonationsdrücker oder -trigger eine Korrektur möglich ist.
- ohne Ventile, wie Naturhorn, Naturtrompete bzw. Barocktrompete zum Teil entscheidende Bedeutung, jedoch ist oft durch verschiedene Anblastechniken auch eine Korrektur möglich. Bei Hörnern ist auch eine Korrektur durch Stopfen (Einführen der Hand in die Stürze) möglich.
Holzblasinstrumente
Die Naturtöne sind hier beim Überblasen von Bedeutung. Auf offenen Flöten und Rohrblattinstrumenten mit konischer Röhre kann auf alle Naturtöne überblasen werden, praktisch wird meist maximal bis zum 4. Naturton überblasen. Eine Ausnahme bilden Obertonflöten (offene Flöten ohne Grifflöcher oder Klappen), auf denen nur die Naturtonreihe spielbar ist. Auf diesen Instrumenten wird bis zum 8. Naturton oder noch höher überblasen. Auf gedackten Flöten und Rohrblattinstrumenten mit zylindrischer Röhre kann nur auf die ungeradzahligen Naturtöne überblasen werden, praktisch wird nur auf den 3. und den 5. Naturton überblasen, da ein Überblasen auf den 7. Naturton nicht nur sehr schwierig ist, sondern auch zu Intonationsproblemen führt, da dieser Ton deutlich von dem entsprechenden gleichstufig gestimmten Ton abweicht.
Saiteninstrumente
Auf Saiteninstrumenten werden höhere Naturtöne als der Grundton durch eine spezielle Spielweise, dem Flageolett, erzeugt.
Orgel
In der Orgel sind die Naturtöne in Form von einzelnen Pfeifenreihen, den Oktavregistern und Aliquotregistern realisiert, die in den unterschiedlichsten Kombinationen eingesetzt werden.
Musiktheorie und Kultur
Die Existenz von Naturtönen oder Obertönen wird seit langer Zeit zu einer wissenschaftlichen Erklärung und Begründung von Tonsystemen der Musik herangezogen. Ein ästhetisches System soll dabei also naturwissenschaftlich legitimiert werden. Die erste dieser Theorien wird Pythagoras zugerechnet, dies war vor rund 2500 Jahren. Einen der letzten Versuche dieser Art findet man bei Hindemith in seiner Unterweisung im Tonsatz. Schon Pythagoras war aber klar, dass kein musikalisches Tonsystem konstruiert werden kann, dass einerseits den Verhältnissen von ganzen Zahlen (den Obertönen, letztlich rationalen Zahlen) und andererseits der Forderung nach der Gleichwertigkeit der Tonschritte (dies erfordert mathematisch geometrische Folgen, also irrationale Verhältnisse) Rechnung trägt. Zweifelsohne ist das moderne, westliche System mit 12 Tönen in gleichschwebender Stimmung ein guter Kompromiss, aber keine Lösung. Deswegen gibt es daneben eine Vielzahl von Stimmungen, die versuchen, die Rauhigkeiten auf andere Weise zu minimieren.
Musikinstrumententechnik, Elektrotechnik und Akustik
Es muss festgestellt werden, dass die sog. "natürlichen Obertöne" mit ihren ganzzahligen Verhältnissen sich nur in einer äußerst künstlich bereiteten Situation – nämlich in hochentwickelten mechanischen Musikinstrumenten, die eindimensionale Schwingungen bevorzugt entwickeln – einstellen, und auch da nur in Näherung. Mechanische Klangerzeuger, wie sie jedes Kind mit Gummibändern zusammenbaut, zeigen, wie dies im anderen Extrem – also schon eher "natürlich" – klingt. Nur elektronische Klangerzeuger erlauben es, ganzzahlige Verhältnisse in Perfektion zu erzeugen, worauf prompt dieser – nun der Musiktheorie nach ideale – Klangcharakter von Musikern negativ bewertet wird.
Mathematisch bleibt hinzuweisen, dass sinusförmige Schwingungen nur dann sinusförmig sind, wenn sie unendlich lange andauern und andauern werden. Die Sinusfunktion erstreckt sich beidseitig in die Unendlichkeit und ein Abschneiden der Dauer führt mathematisch zu etwas Anderem, dem Wellikel, einer zeitlich begrenzten Welle. Diese besitzt aber keine scharf voneinander abgegrenzten Obertöne mehr, sondern ein verschmiertes Frequenzband. In psychoakustischer Konsequenz ergeben sich beim Abschneiden von langandauernden, statischen Sinustönen oder Sinustongemischen breitbandige Artefakte. Bei kurzandauernden Vorgängen solcher Art – wie sie bei allen Instrumenten auftreten, bei denen nicht stets Energie nachgereicht wird, also vor allem den Zupf- und Schlaginstrumenten (auch dem Klavier) – ist die Grundvoraussetzung des Dauertones noch nicht einmal mehr in Näherung gegeben.
In der Kultur der Ingenieurwissenschaften ging man meist von der Situation aus, dass Vorgänge langandauernd und langsam veränderlich sind (bei der Modulation eines Radiosenders ist dies der Fall). Nur dann ergeben die Fouriertransformation und die daraus implizit im Artikel folgenden Begriffe einen Sinn. Erst in den letzten Dekaden hat sich die Einsicht durchgesetzt, dass bei schnell veränderlichen und kurz andauernden Vorgängen die Wavelet-Transformation Anwendung finden muss, worauf Begriffe wie etwa Frequenz neu gedeutet werden müssen.
Musik beinhaltet wesentlich solche Vorgänge. Insofern ist auch aus dieser Sicht Kritik an überkommenen Vorstellungen zu üben.
Literatur
- Michael Dickreiter: Handbuch der Tonstudiotechnik. 6. Auflage, K.G. Saur Verlag KG, München, 1997, ISBN 3-598-11320-x
Siehe auch
Wikimedia Foundation.