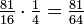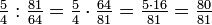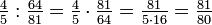Naturtonleiter

Reine Stimmungen (auch natürliche oder harmonische Stimmungen) verwenden im Gegensatz zur pythagoreischen Stimmung nicht nur die reinen Intervalle Oktave, Quinte und daraus folgend die Quarte, sondern auch solche höherer Ordnung, wie sie sich aus der Obertonreihe ergeben, beispielsweise die große Terz oder, seltener, die Naturseptime.

Abgrenzung

Teilweise wird auch von einer reinen „Stimmung“ gesprochen, wenn im A-cappella-Gesang oder bei Instrumenten ohne fixierter Tonhöhe (etwa bei bundlosen Saiteninstrumenten), sowohl in der abendländischen Musiktradition als auch in außereuropäischen Musikkulturen, harmonisch-rein intoniert wird.

Im musikwissenschaftlichen Sinn ist der Begriff reine Stimmung im weiteren Sinn das harmonisch-reine Tonsystem, welches den Obertönen entsprechend über (theoretisch) unendlich viele Tonstufen verfügt und als rein „gedachtes“ Beziehungsgeflecht einzelner Tonigkeiten in der Dur-/Moll-tonalen Musik fungiert, aber auch in außereuropäischer Musik vorkommt. Da unendlich viele Tonstufen in der musikalischen Praxis nicht reproduzierbar sind, versteht man im engeren Sinn eine zwölfstufige Auswahl (etwa für Tasteninstrumente) aus diesem System und nennt diese harmonisch-reine Stimmung.

Letztere haben in der abendländischen Musikpraxis jedoch kaum eine Bedeutung erlangt, da sie nicht nur bei der Modulation in entfernte Tonarten, sondern bereits bei diatonischen Skalen und einstimmigen Melodien erhebliche Mängel aufweisen. Doch waren für diverse Temperierungen, wie etwa die mitteltönige Stimmung und verschiedene mikrotonale Tonsysteme sowohl ihre – auf einen Grundton bezogen – absolut sauber klingenden Intervalle ein idealisiertes Ziel, dem man möglichst nahe zu kommen versuchte, als auch die Entwicklungsgrundlage.

Beispiel

Obertonpositionen

Die C-Dur-Tonleiter in reiner Stimmung (Beispiel) C beruht auf folgenden Frequenzverhältnissen zwischen den Tönen:

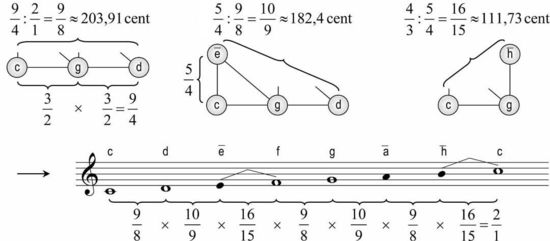
Name des Tones	C	D	E	F	G	A	H	c
Frequenzverhältnis zum Grundton	1/1	9/8	5/4	4/3	3/2	5/3	15/8	2/1
Frequenzverhältnis zum vorigen Ton	16/15	9/8	10/9	16/15	9/8	10/9	9/8	16/15

Dadurch weicht diese Tonleiter unüberhörbar von der C-Dur-Tonleiter in pythagoreischer Stimmung und auch von der Tonleiter in gleichmäßig-temperierter Stimmung ab, bei der jeder Halbton genau ein Zwölftel der Oktave ausmacht und ein Ganzton genau zwei Halbtönen entspricht.

Historische Entwicklung

Dieser Artikel oder Abschnitt bedarf einer Überarbeitung. Näheres ist auf der Diskussionsseite angegeben. Hilf mit, ihn zu verbessern, und entferne anschließend diese Markierung.

Das Quint-Terz-Schema

Die Einführung der reinen Großterz (mit dem Saitenlängenverhältnis zwischen unterem und oberem Ton von 5:4) – als Ersatz und Vereinfachung des pythagoreischen Ditonus (81:64) – geht zurück auf die enharmonische Tetrachordteilung Didymos' (etwa 100 Jahre nach Pythagoras).

In der abendländischen Musik wurde die reine Großterz emanzipiert, indem sie zusammen mit der Sexte (8:5) im 15. Jahrhundert nicht mehr als Dissonanz, sondern als zunächst noch unvollkommene Konsonanz aufgefasst wurde und vor allem als Bestandteil des Dreiklanges zunehmend an musikalischer Bedeutung gewann. Die Deutung der Großterz als 5. Oberton in der Natur- bzw. Teiltonreihe, sowie des Durdreiklanges als Zusammenklang von 4., 5. und 6. Oberton ist dabei eine (umstrittene) Definition der Neuzeit.

In den folgenden Darstellungen und Berechnungen werden die Intervalle - wenn nicht ausdrücklich anders beschrieben - als Frequenzverhältnisse der Intervalltöne in Brüchen dargestellt, wobei die größere Zahl im Zähler für den höheren und die kleinere Zahl im Nenner für den tieferen Ton steht.

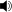  C-Dur Akkord in der Obertonreihe^?/i

Wie jedes Tonsystem basiert auch das harmonisch-reine auf axiomatischen Intervallen, die als gegeben betrachtet werden. Das sind hier die Oktave ²/₁, Quinte ³/₂ und Terz ⁵/₄. Die anderen Intervalle das Tonsystems lassen sich so als Produkte und Quotienten dieser Intervalle darstellen. Dabei ist das mehrfache Auftauchen in dem Produkt oder dem Quotienten möglich.

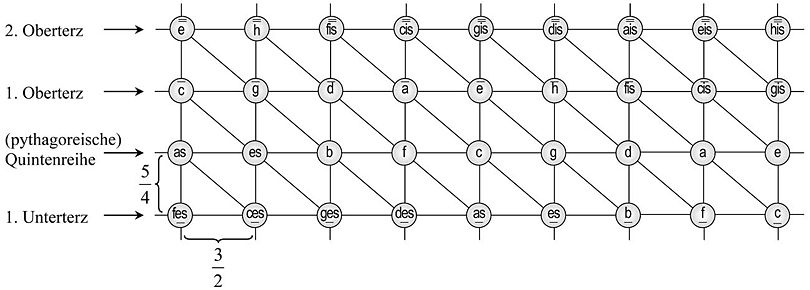
So ergibt sich aus der Vielzahl von Kombination dieser Intervalle ein (theoretisch) unendlicher Tonraum, der sich mittels eines Tonnetzes wie folgt grafisch darstellen lässt:

Darstellung im Tonnetz

Diese grafische Darstellung des Quint-Terz-Schemas versteht sich als Beziehungsgeflecht von Tonigkeiten ohne fixierter Oktavlage (auch: „Chroma“, „Toncharakter“ ^[1]; engl.: „pitch class“), so dass zur Berechnung konkreter Intervallverhätnisse noch das entsprechende Vielfache der Oktave ²/₁ hinzu- oder weggenommen werden muss. Etwa bis zur Mitte des 19. Jahrhunderts galten die Oktave, die reine Quinte und Terz, sowie sämtliche Intervalle, die aus deren Kombination resultieren, als von der jeweiligen Stimmung unabhängiges, eigentlich „gemeintes“ Tonsystem der Dur-/Moll-tonalen Musik und das „Tonnetz“ als entsprechende Abbildung dieser Tonbeziehungen. Durch die zunehmende Alterations-Harmonik, enharmonische Verwechslungen und Ganztonskalen ist eine solche Trennung von „gedachtem System“ und „realisierbarer Stimmung“ (spätestens) ab der Spätromantik nicht mehr gegeben, da derartige Phänomene nicht nur pragmatisch, sondern auch (musik-)theoretisch die gleichschwebende Temperatur voraussetzen.

Das eigentliche „Tonnetz“ wurde 1773 von Leonhard Euler als speculum musicum („Abbild der Musik“) in seiner gleichnamigen Schrift „De harmoniae veris principiis per speculum musicum repraesentatis“ ^[2] vorgestellt, und von da an – zusammen mit den von Moritz Hauptmann ^[3] eingeführten „Kommastrichen“ a, e, h und des, as, es, usw. – von zahlreichen Theoretikern zu verschiedenen Zwecken abgewandelt (u. a. von Hermann v. Helmholtz ^[4], Arthur v. Oettingen ^[5] und Hugo Riemann ^[6]). Die unterschiedlichen Charaktere von Tönen gleichen Namens aber verschiedener Lage im (unendlichen) Tonraum ergibt sich in harmonisch-reiner Stimmung nicht nur aus einer jeweils anderen Tonumgebung und Harmonisierung (etwa das e im C-dur-Akkord c-e-g und das e im E-dur-Akkord e-gis-h), sondern auch aus einem (minimalem) Tonhöhenunterschied zwischen den jeweiligen Tonstufen (e und e):

Über c liegt seine Terz ⁵/₄ e. In der Quintenreihe von c liegt aber auch ein e; als 4. Oberquinte von c kommt ihm das Tonverhältnis ⁸¹/₁₆ zu (3⁴/2⁴). Wird diese Oberquinte um 4 Oktaven nach unten verschoben, so dass sie bei ⁵/₄ e liegt, ergibt sich ihr Tonverhältnis zu c wie folgt:

$\tfrac{81}{16} \cdot \tfrac{1}{4} = \tfrac{81}{64}$

Vergleichen wir die beiden e miteinander,

$\tfrac{5}{4} : \tfrac{81}{64} = \tfrac{5}{4} \cdot \tfrac{64}{81} = \tfrac{5 \cdot 16}{81} = \tfrac{80}{81}$

zeigt sich, dass der Tonhöhenunterschied ⁸⁰/₈₁ beträgt. Er wird syntonisches Komma genannt.
Die 80 ist der Terz ⁵/₄ e zuzuordnen (⁵/₄ = ⁸⁰/₆₄), also ist ⁵/₄ e [um ca. 21,51 Cent, bzw. etwa einen Zehntel-Ton] tiefer als das gleichnamige ⁸¹/₆₄ e“ ^[7]

Umgekehrt liegt das as (etwa im f-Moll-Akkord f-as-c) ein syntonisches Komma über der gleichnamigen Tonstufe in der Quintenkette as-es-b-f-c:

$\tfrac{4}{5} : \tfrac{64}{81} = \tfrac{4}{5} \cdot \tfrac{81}{64} = \tfrac{81}{5 \cdot 16} = \tfrac{81}{80}$

Die C-Dur-Tonleiter in harmonisch-reiner Quint-Terz Stimmung

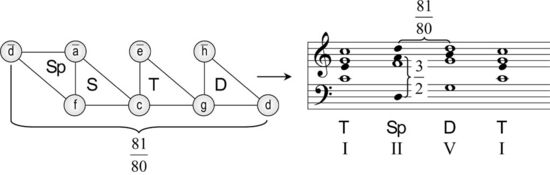
Die reine C-Dur-Tonleiter kann verstanden werden als Auswahl derjenigen sieben Tonstufen aus dem Quint-Terz-Schema, die zur Intonation der drei Hauptfunktionen Subdominante (S), Tonika (T) und Dominante (D) – also für die „authentische“ Kadenz benötigt werden:

  C-Dur-Tonalität^?/i

Die eigentliche Skala entsteht durch Transposition dieser Tonstufen in die entsprechende Oktavlage – beispielsweise zwischen c¹ und c². Sie besteht nun – im Gegensatz zur pythagoreischen Skala – nicht mehr aus zwei, sondern aus drei Intervallschritten verschiedener Größe, dem großen Ganzton ⁹/₈, dem kleinen Ganzton ¹⁰/₉ und dem diatonischen Halbton ¹⁶/₁₅ :

  reine C-Dur-Tonleiter^?/i

Diese siebenstufige Tonleiter erlaubt nun zwar die harmonisch-reine Intonation der Hauptfunktionen T, S und D, doch wirkt sie melodisch unsauber, da die jeweiligen Terzen e, a und h in melodischen Zusammenhang als zu niedrig empfunden werden können. Insbesondere der Leitton h-c ist mit seinen 111,73 Cent problematisch, da er der Tendenz widerspricht, die Strebewirkung von Leittönen durch eine möglichst enge Intonation zu erhöhen (beispielsweise durch das pythagoreische Limma h-c ²⁵⁶/₂₄₃ zu 90,22 Cent). Viele der Intonationsschwierigkeiten – etwa von Streichern, die häufig geschärfte Terzen bzw. Leittöne spielen, und Bläsern – lassen sich auf die Unvereinbarkeit von harmonischer und quasi pythagoreisch-melodischer Reinheit zurückführen.

„In didymischer Auffassung ist cis tiefer als des, gis tiefer als as, dis tiefer als es, usw. Eine Bewertung, die dem melodischen Schrittempfinden des instinktiven Musikers durchaus widerspricht! Und in der Tat ist die naturgewollte primäre Terz gar kein melodisches, sondern ein harmonisches Intervall. […] Die griechische, mathematisch orientierte Musiktheorie zählte die pythagoreische Terz den Dissonanzen zu. Sie hatte in dem Sinne recht, als der Begriff der Konsonanz und Dissonanz ja durchaus eine harmonische Wertung ist. […] Die Linearität der Melodie hat nichts mit großen und kleinen Ganztönen, mit Kommadifferenzen und dergleichen zu schaffen.“ − Sigfrid Karg-Elert  ^[8]

Die zwei verschieden großen Ganztöne ⁹/₈ und ¹⁰/₉ – die Auslöser dieses „Konflikts“ – ergeben sich (zwangsläufig) aus der arithmetischen Teilung der (reinen) Großterz ⁵/₄. Deren Differenz entspricht dem sog. syntonischen, oder didymischem Komma ⁸¹/₈₀ mit ca. 21,51 Cent; d. h. die Tonstufen, die in der Reihe über den (gleichnamigen) Tonstufen im Tonnetz liegen werden etwa einen Zehntel-Ton tiefer als diese intoniert (e:e = 80:81). Eine Lösung dieses zusätzlichen Problems liefert die mitteltönige Stimmung mit der geometrischen Teilung der Großterz, was zu zwei gleichgroßen Ganztönen (jeweils 193,156 Cent) führt, ohne die Reinheit der Terz in Frage zu stellen.

Die „zweierlei d in C-Dur“

Ein anderes Problem besteht in der Intonation der Quinte d-a, die als Wolfsquinte ⁴⁰/₂₇ zu 680,448 Cent um ein syntonisches Komma zu eng, und damit dissonant erscheint. Sie erklingt u. a. im d-Moll-Akkord (d-f-a) auf der zweiten Stufe bzw. in der Kadenz mit Subdominantparallele (T-Sp-D-T):

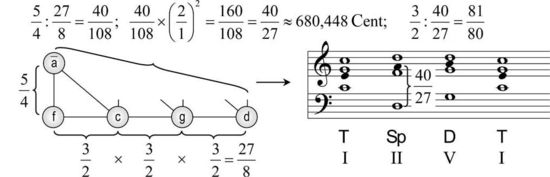
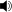  dissonantes d-Moll in C-Dur^?/i

Die Bereinigung dieses dissonanten Intervalls erfordert eine zusätzliche Tonstufe d (d:a= 2:3 statt d:a = 27:40), wodurch allerdings das syntonische Komma ⁸¹/₈₀ zu einem musikalisch relevanten (hörbaren) Intervallschritt wird:

  zweierlei d in C-Dur^?/i

Noch deutlicher tritt das Mikrointervall zwischen d und d in Erscheinung, wenn die C-Dur-Tonleiter entsprechend modifiziert wird:

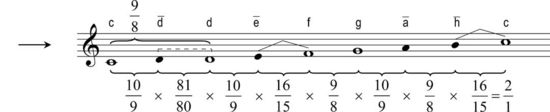
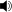  achtstufige C-Dur-Tonleiter^?/i

Diese achtstufige Tonleiter erlaubt nun zwar die harmonisch-reine Intonation sämtlicher diatonischer Nebenfunktionen in C-Dur, doch widerspricht sie nicht nur der gängigen Musikpraxis, sondern auch dem, was im Allgemeinen unter dem diatonischen Tonsystem verstanden wird, bzw. dem, was Hörer und Komponist unter der diskreten Tonhöhenkategorie oder Tonigkeit „d“ erwarten.

Dessen ungeachtet stehen in einigen mikrotonalen Systemen tatsächlich beide Tonstufen d und d zur Verfügung.

Erweiterte reine Stimmung

Später wurde die reine Stimmung eher aus theoretischen als aus musikalisch-praktischen Beweggründen auf zwölf Töne erweitert.

Die zwölftönige Skala ergibt sich durch Hinzufügen von fünf weiteren Tönen, die so gewählt werden, dass C inmitten der Quintenreihe b–f–c–g–d steht und die Töne dieser Reihe (Rangordnung: c–g–f–d–b) nach Möglichkeit von diatonischen Halbtönen (¹⁶/₁₅) umgeben sind. Es treten ausschließlich ganzzahlige Frequenzverhältnisse auf.

Name	Frequenz- verhältnis zum vorherigen Ton	Frequenz- verhältnis zum Grundton	Quotient	Intervall	Beziehung zur Quinten- spirale
c	16/15	1/1	1	0 C
des	16/15	16/15	1,06	111,731 C	gr. Terz unter f
d	135/128	9/8	1,125	203,910 C
es	16/15	6/5	1,2	315,641 C	gr. Terz unter g
e	25/24	5/4	1,25	386,314 C	gr. Terz über c
f	16/15	4/3	1,3	498,045 C
fis	135/128	45/32	1,40625	590,224 C	gr. Terz über d
g	16/15	3/2	1,5	701,955 C
as	16/15	8/5	1,6	813,686 C	gr. Terz unter c
a	25/24	5/3	1,6	884,359 C	gr. Terz über f
b	16/15	16/9	1,7	996,090 C
h	135/128	15/8	1,875	1088,269 C	gr. Terz über g
c	16/15	2/1	2	1200 C

Veranschaulichung

Chromatisch

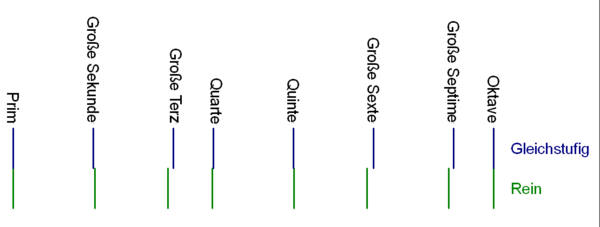
In der Abbildung sind die Frequenzverhältnisse der reinen und der gleichstufigen Stimmung bei einer chromatischen Tonleiter grafisch gegenübergestellt:

Insbesondere bei den Terzen und den Sexten sind deutliche und gegenläufige Abweichungen vorhanden. Bei der gleichstufigen Stimmung sind die kleine Terz, die kleine Sexte und die Sekunden kleiner, die große Terz, die große Sexte und die Septimen größer.

Dur

Bei einer Dur-Tonleiter wirkt sich dies wie folgt aus:

Die Terz, die Sexte und die Septime sind bei der gleichstufigen Stimmung zu groß.

Reines Moll

Bei einer reinen Moll-Tonleiter ist es anders:

Die Terz und die Sexte sind bei der gleichstufigen Stimmung zu klein.

Bezeichnungen der Halbtöne

Die Abstände benachbarter Töne (Halbtöne) haben folgende Bezeichnungen und Werte:

Name	Frequenzverhältnis	Intervall	Beispiel
Diatonischer Halbton	16/15	111,731 C	e – f
Großer chromatischer Halbton	135/128	92,179 C	f – fis
Kleiner chromatischer Halbton	25/24	70,672 C	es – e

Zu beachten: Diese Skala ist nicht für die reine Moll-Tonleiter geeignet, da das Intervall es–b keine reine Quinte darstellt.

Einsatzgebiete

Über den praktischen Sinn dieser zwölftönigen Stimmung lässt sich streiten, denn sie ist auf keinen Fall so flexibel einsetzbar wie die gleichstufige Stimmung. Es gibt aber mindestens zwei Arten, sie in sinnvoller Weise zu benutzen. Die erste Art ist, in den zentralen Tonarten zu bleiben und gewisse Restriktionen zu beachten. Auf diese Weise bekommt man eine (für viele Ohren) sehr harmonisch klingende Musik, ist aber in der Komposition bzw. Stückauswahl recht beschränkt. Die zweite Art ist, alle möglichen Klänge, also sowohl die extremen Dissonanzen als auch die extremen Konsonanzen dieser Stimmung zuzulassen und so speziell für diese eine Stimmung, aber ohne Einschränkungen, zu komponieren.

Ein Beispiel für die erste Art ist, modulierenderweise in der C-Dur- oder G-Dur-Skala zu bleiben, dabei aber, für C-Dur, das D in manchen Zusammenhängen zu unterlassen, und für G-Dur, das A in manchen Zusammenhängen zu unterlassen. Als Beispiel für die zweite Art sei hier die CD the harp of new albion von Terry Riley genannt. Diese Pianosoloaufnahme verwendet einen Flügel mit der in diesem Artikel genannten erweiterten Stimmung, nur ist die Grundlage das Cis und nicht das C, und es wird der Tritonus ⁶⁴/₄₅ benutzt.

Klangbeispiele

Für die klangliche Darstellung reiner Stimmungen wurde ein bekanntes, freilich historisch nicht korrektes Beispiel gewählt, das es möglich macht, die diffizilen Unterschiede deutlich zu hören. Es wurde von Johann Sebastian Bach für eine der (vielen) wohltemperierten Stimmungen konzipiert; für welche genau lässt sich heute nicht mehr mit Sicherheit rekonstruieren.

Johann Sebastian Bach: Präludium in C-Dur aus dem ersten Band des Wohltemperierten Klaviers, BWV 846

Beispiel 1: Takte 1 bis 5

• Die im Text beschriebene 7stufige (reine) C-Dur-Tonleiter führt zwar zu einem melodisch sinnvollen großen Ganzton (⁹/₈) c-d [bei a)], doch wird die Quinte d-a [bei b)] dadurch unrein (⁴⁰/₂₇ statt ³/₂, sie ist mit ca. 680,448 Cent um ein syntonisches Komma zu klein).  Anhören^?/i

• Durch Erweiterung der Skala um ein erniedrigtes d [bei a)] wird die Quinte d-a [bei b)] nun zwar bereinigt, doch entsteht zum einen ein unmelodischer kleiner Ganzton (¹⁰/₉) und zum anderen eine deutlich hörbare (syntonische) Kommadifferenz (⁸¹/₈₀) zwischen den d's des zweiten und des dritten Taktes [bei c)].  Anhören^?/i

• Bei Annahme der Naturseptime (⁷/₄ statt ⁹/₅) im Dominantseptakkord [bei d)] entsteht ein zusätzliches „septimales Komma“ (⁶⁴/₆₃, ca. 27,264 Cent) zwischen dem f des zweiten und des dritten Taktes [bei e)]. Der Gleitton f-e wird als „septimaler Halbton“ (²¹/₂₀, ca. 84,467 Cent) eng intoniert [bei f)].  Anhören^?/i

Beispiel 2: Takte 5 bis 11

• Auch die 12stufige, chromatische Skala beinhaltet (nur) die unreine Quinte d-a (⁴⁰/₂₇), die hier zweimal als Teil des Doppeldominant-Septakkordes erklingt [bei a)].  Anhören^?/i

• Der Ausgleich dieser Quinte erfordert nun ein pythagoreisch eingestimmtes a (²⁷/₁₆ statt ⁵/₃), das gegenüber dem a als Grundton der Tonikaparallele um ein syntonisches Komma erhöht ist [bei b)]. Da die Kommadifferenzen hier in einer der Mittelstimmen erklingen fallen sie kaum ins Gewicht – mit einem durchaus annehmbaren klanglichen Resultat.  Anhören^?/i

• Im Gegensatz dazu führt der als Naturseptime intonierte Ton c der Doppeldominante wiederum zum deutlich hörbaren „septimalen Komma“ [bei c)].  Anhören^?/i

Quellen

1. ↑ vgl.: Jacques Handschin: Der Toncharakter. Eine Einfuhrung in die Tonpsychologie; Zürich, 1948
2. ↑ Leonhard Euler: De harmoniae veris principiis per speculum musicum repraesentatis, veröffentlicht in Novi Commentarii academiae scientiarum Petropolitanae 18, St. Petersburg, 1774
3. ↑ Moritz Hauptmann: Die Natur der Harmonik und Metrik, Leipzig, 1853
4. ↑ Hermann v. Helmholtz: Die Lehre von den Tonempfindungen als physiologische Grundlage für die Theorie der Musik, Braunschweig, 1863
5. ↑ Arthur von Oettingen: Harmoniesystem in dualer Entwicklung. Studien zur Theorie der Musik, Dorpat u. Leipzig, 1866; überarbeitete zweite Auflage als Das duale Harmoniesystem, Leipzig, 1913
6. ↑ z.B.: Hugo Riemann: Ideen zu einer „Lehre von den Tonvorstellungen“, in: Jahrbuch Peters 21/22, 1914/15
7. ↑ Martin Vogel: Die Lehre von den Tonbeziehungen, Bonn – Bad Godesberg, 1975, S. 103f
8. ↑ Sigfrid Karg-Elert: Polaristische Klang- und Tonalitätslehre. Leipzig, 1930, S. 6f

Siehe auch

• Cent

Stimmungen des abendländischen zwölfstufigen Tonsystems
Aulos-Modi | Pythagoreische Stimmung | Reine Stimmung | Mitteltönige Stimmung | Wohltemperierte Stimmung | Werckmeister-Stimmung | Silbermann-Sorge-Temperatur | Kirnberger-Stimmung | Gleichstufige Stimmung | Vallotti-Stimmung