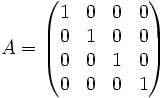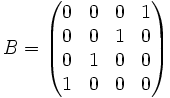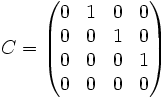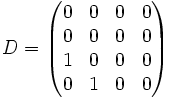Nebendiagonale

In der linearen Algebra ist eine Diagonale einer quadratischen Matrix eine Linie, die schräg durch das Koeffizientenschema geht. Die Hauptdiagonale verläuft von oben links nach unten rechts, die Nebendiagonale von oben rechts nach unten links. Verschiebt man die Hauptdiagonale nach rechts oder unten, so erhält man Linien, die man ebenfalls Nebendiagonalen nennt. Eine nach rechts verschobene Nebendiagonale nennt man obere Nebendiagonale, eine nach unten verschobene nennt man untere Nebendiagonale. Spricht man nur von der k-ten Nebendiagonale, meint man meist die k-te obere Nebendiagonale. Die unteren Nebendiagonalen werden dann mit Hilfe negativer Werte von k bezeichnet.

In der folgenden Matrix bilden die Elemente mit dem Wert 1 die Hauptdiagonale:

$A = \begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{pmatrix}$

In der folgenden Matrix bilden die Elemente mit dem Wert 1 die Nebendiagonale:

$B = \begin{pmatrix} 0 & 0 & 0 & 1\\ 0 & 0 & 1 & 0\\ 0 & 1 & 0 & 0\\ 1 & 0 & 0 & 0 \end{pmatrix}$

In der folgenden Matrix bilden die Elemente mit dem Wert 1 die erste (obere) Nebendiagonale:

$C = \begin{pmatrix} 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 \end{pmatrix}$

In der folgenden Matrix bilden die Elemente mit dem Wert 1 die zweite untere (oder -2te) Nebendiagonale:

$D = \begin{pmatrix} 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 \end{pmatrix}$

Formal lassen sich die Diagonalen einer $n \times n$-Matrix A = (a_ij)_{i,j = 1,...,n} wie folgt beschreiben:

die Hauptdiagonale (a_ii),i = 1,...,n,

die Nebendiagonale (a_{i,n + 1 − i}),i = 1,...,n, teilweise heißt diese auch Gegendiagonale

die k-te obere Nebendiagonale (a_{i + k,i}),i = 1,...,n − k,

die k-te untere Nebendiagonale (a_{i,i + k}),i = 1,...,n − k.

Verallgemeinerung

Die Hauptdiagonale einer nichtquadratischen 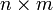$n \times m$-Matrix A = (a_ij)_{i = 1,...,n,j = 1,...,m} besteht aus den Elementen a_ii.

Anmerkungen

Eine quadratische Matrix, bei der nur die Elemente auf der Hauptdiagonalen von null verschieden sind, heißt Diagonalmatrix. Sind diese Elemente auch noch alle 1, so spricht man von einer Einheitsmatrix.

Die Summe der Elemente der Hauptdiagonalen nennt man Spur der Matrix.