Newton-Darstellung

Unter Polynominterpolation versteht man die Lösung der Aufgabe, ein Polynom zu finden, das exakt durch vorgegebene Stützstellen verläuft und diese damit interpoliert. Für n + 1 gegebene Wertepaare 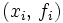$(x_i,\,f_i)$ mit paarweise verschiedenen x_i gibt es genau ein Polynom P(x) maximal n-ten Grades, das alle Gleichungen P(x_i) = f_i erfüllt. Dieses Polynom wird Interpolationspolynom genannt.

Ein Polynom n-ten Grades hat n+1 Koeffizienten, also ebenso viele Freiheitsgrade. Die Lösung des Interpolationsproblems kann damit durch ein lineares Gleichungssystem bestimmt werden. Wie dieses Gleichungssystem aussieht, hängt von der gewählten Darstellung beziehungsweise Basis ab. Die Eindeutigkeit folgt daraus, dass ein Polynom n-ten Grades mit reellen oder komplexen Koeffizienten, das nicht das Nullpolynom ist, höchstens n Nullstellen hat. Die Differenz zweier verschiedener Lösungen wäre aber an allen n+1 Interpolationsstellen gleich 0.

Newton-Basis

Die so genannte Newton-Basis hat sich zur Darstellung und Auswertung bewährt. Dabei ist das Interpolationspolynom gegeben durch

$P(x) = \sum_{k=0}^{n} c_{k}N_{k}(x)$

mit den Newton-Basis-Funktionen

$N_{k}(x) = \begin{cases} 1, & k=0 \\ \prod_{j=0}^{k-1}(x-x_{j}), & k\ge 1. \end{cases}.$

Die unbekannten Koeffizienten c_k können hier mit Hilfe des „Schemas der dividierten Differenzen“ effizient und numerisch stabil berechnet werden. Es gilt

$c_k = [x_0, \dots, x_k]f$,

wobei die dividierten Differenzen durch die Rekursion (i < j)

$i = 0 \qquad f_i = [x_i]f \qquad$

$i = 1, \ldots, n \qquad [x_i,\dots,x_j]f = \frac {[x_{i+1},\dots,x_j]f-[x_i,\dots,x_{j-1}]f}{x_j - x_i}$

aus den Stützwerten $f_i = [x_i]f\,$ bestimmt werden.

Wenn das Feld x die Stützstellen x(1)...x(n) und das Feld y die Stützwerte y(1) bis y(n) enthält, dann liefert der folgende BASIC-Algorithmus die Koeffizienten c₁,c₂,...,c_n. Die Programmsequenz verändert dazu das Feld y derart, dass der Koeffizient c₁ in y(1) steht, c₂ in y(2) bis c_n in y(n).

   For i = 1 To n
       For j = n To i + 1 Step -1
           y(j) = (y(j) - y(j-1)) / (x(j) - x(j-i))
       Next j
   Next i

Das folgende Programm liefert, ausgehend von den oben berechneten Koeffizienten und Stützstellen, den Wert der Interpolationsfunktion an der Stelle x_Wert. Ferner ist die Auswertung eines Polynoms in Newton-Darstellung mittels des Horner-Schemas in linearem Zeitaufwand möglich.

   y_Wert = y(n+1)
   For i = n To 1 Step -1
       y_Wert = y_Wert * (x_Wert - x(i)) + y(i)
   Next i

Lagrange-Basis

Eher für theoretische Betrachtungen günstig ist eine Darstellung in der Lagrange-Basis. Hier nennt man die Basisfunktionen Lagrange-Polynome:

$\ell_{i}(x) = \prod_{j=0, j \neq i}^{n} \frac{x-x_{j}}{x_{i}-x_{j}}.$

Sie sind so definiert, dass

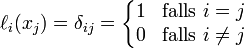$\ell_i(x_j) = \delta_{ij} = \left\{\begin{matrix} 1 &amp;amp; \mbox{falls } i=j \\ 0 &amp;amp; \mbox{falls } i \neq j \end{matrix}\right.$ gilt,

wobei 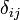$\delta_{ij}\,$ das Kronecker-Delta darstellt. Die Lösung des Interpolationsproblems lässt sich dann einfach angeben als

$P(x) = \sum_{i=0}^{n} f_i\ell_{i}(x).$

Dies wird häufig benutzt, um die Existenz der Lösung des Interpolationsproblems zu beweisen.

Der große Vorteil der Newton-Basis ist, dass sich dort neue Punkte sehr leicht einfügen lassen, indem man einfach am Ende noch einen Term anhängt. Bei der Lagrange-Basis muss man alle Basisfunktionen komplett neu berechnen.

Probleme

Polynome haben den Nachteil, dass sie viele Extrema haben und deswegen bei hohem Polynomgrad recht stark schwingen, weswegen es manchmal vorteilhaft ist, das Interpolationspolynom aus Teil-Polynomen zusammenzusetzen (siehe Runges Phänomen und Spline-Interpolation).

Anwendungen

Polynome lassen sich sehr leicht integrieren und ableiten. Deswegen tauchen interpolierende Polynome an vielen Stellen in der numerischen Mathematik auf, beispielsweise bei der numerischen Integration und entsprechend bei Verfahren zur numerischen Lösung gewöhnlicher Differentialgleichungen.

Literatur

• Hans R. Schwarz, Norbert Köckler: Numerische Mathematik, 5. Aufl., Teubner, Stuttgart 2004, ISBN 3-519-42960-8

Weblinks

• Seite zu Newton, Lagrange und Cubic Spline mit Java Applet
• Erläuterungen und Beispiel zur Lagrange-Interpolation