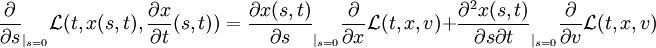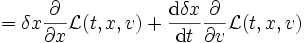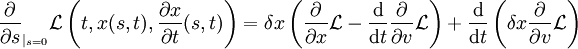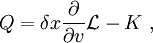- Noether Theorem
-
Das Noether-Theorem verknüpft elementare physikalische Begriffe wie Ladung, Energie und Impuls mit geometrischen Eigenschaften, der Invarianz der Wirkung unter Symmetrietransformationen. Es wurde 1918 von Emmy Noether formuliert:
-
- Zu jeder kontinuierlichen Symmetrie eines physikalischen Systems gehört eine Erhaltungsgröße und umgekehrt.
Dabei ist eine Symmetrie eine Transformation (zum Beispiel eine Drehung oder Verschiebung), die das Verhalten des physikalischen Systems nicht ändert.
Eine Erhaltungsgröße E eines Systems von Teilchen ist eine Funktion der Zeit t, des Ortes x der Teilchen und ihrer Geschwindigkeit v, deren Wert sich auf jeder physikalisch durchlaufenen Bahn x(t) nicht mit der Zeit ändert. Zum Beispiel ist die Energie
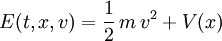 eines Teilchens der Masse m, das sich in einem Potential V bewegt, eine Erhaltungsgröße,
eines Teilchens der Masse m, das sich in einem Potential V bewegt, eine Erhaltungsgröße,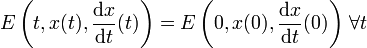 .
.
Inhaltsverzeichnis
Beispiele für Symmetrien und zugehörige Erhaltungsgrößen
- Aus der Homogenität der Zeit (Wahl der Startzeit spielt keine Rolle) folgt die Erhaltung der Energie (Energieerhaltungssatz). So bleibt die Energie eines Pendels bei Vernachlässigung von Reibung erhalten, nicht aber die Energie einer Schaukel, auf der ein Kind durch Heben und Senken seines Körpers die Länge von der Aufhängung bis zum Schwerpunkt zeitlich verändert.
- Aus der Homogenität des Raums (Wahl des Startpunktes spielt keine Rolle), ergibt sich die Erhaltung des Impulses (Impulserhaltungssatz). So bleibt der Impuls eines freien Teilchens erhalten, nicht aber der Impuls eines Teilchens im Gravitationsfeld der Sonne. Ihr Ort ist für die Bewegung des Teilchens wesentlich.
- Aus der Isotropie des Raums, sprich der Dreh- bzw. Rotationsinvarianz (Richtung im Raum spielt keine Rolle), ergibt sich die Erhaltung des Drehimpulses (Drehimpulserhaltungssatz). So bleibt der Drehimpuls eines Teilchens im Gravitationsfeld der Sonne erhalten, denn das Gravitationspotential
 ist in allen Richtungen gleich.
ist in allen Richtungen gleich.
- Weil sich ein freies Teilchen der Masse m unverändert mit gleichförmiger Geschwindigkeit v bewegt, wenn es ein gleichförmig bewegter Beobachter betrachtet, ist der gewichtete Startort,
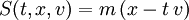 , eine Erhaltungsgröße, S(t,x(t),v(t)) = mx(0). Auf mehrere Teilchen verallgemeinert folgt, dass sich der Schwerpunkt mit gleichförmiger Geschwindigkeit bewegt, wenn die Gesamtkraft verschwindet.
, eine Erhaltungsgröße, S(t,x(t),v(t)) = mx(0). Auf mehrere Teilchen verallgemeinert folgt, dass sich der Schwerpunkt mit gleichförmiger Geschwindigkeit bewegt, wenn die Gesamtkraft verschwindet.
Umgekehrt gehört in der Lagrangeschen Mechanik zu jeder Erhaltungsgröße eine Symmetrie der Wirkung.
Die Symmetrien, die zur Erhaltung der elektrischen Ladung und anderer Ladungen von Elementarteilchen gehören, betreffen Wellenfunktionen von Elektronen, Quarks und Neutrinos. Jede solche Ladung ist ein lorentzinvarianter Skalar, das heißt, sie hat in allen Bezugssystemen denselben Wert, anders als beispielsweise der Drehimpuls, die Energie oder der Impuls.
Mathematische Formulierung
Wirkung
Der im Noether-Theorem formulierte Zusammenhang von Symmetrien und Erhaltungsgrößen gilt für solche physikalischen Systeme, deren Bewegungs- oder Feldgleichungen aus einem Variationsprinzip abgeleitet werden können. Die Differentialgleichungen, denen solche Systeme genügen, besagen, dass die Variation eines Wirkungsfunktionals verschwindet.
Bei der Bewegung von Massepunkten ist dieses Wirkungsfunktional durch eine Lagrangefunktion der Zeit t, des Ortes x und der Geschwindigkeit v
charakterisiert und ordnet jeder differenzierbaren Bahnkurve
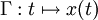 das Zeitintegral
das Zeitintegralzu. Beispielsweise ist in Newtonscher Physik die Lagrangefunktion eines Teilchens im Potential V die Differenz von kinetischer und potentieller Energie
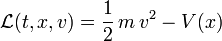 .
.
Die physikalisch tatsächlich durchlaufene Bahn, die zur Anfangszeit t1 durch den Startpunkt
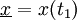 und zur Endzeit t2 durch das Ziel
und zur Endzeit t2 durch das Ziel 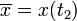 geht, macht den Wert der Wirkung im Vergleich mit allen anderen (differenzierbaren) Bahnen, die ebenfalls anfänglich durch
geht, macht den Wert der Wirkung im Vergleich mit allen anderen (differenzierbaren) Bahnen, die ebenfalls anfänglich durch 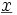 und schließlich durch
und schließlich durch 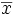 gehen, stationär. Die physikalisch tatsächlich durchlaufene Bahn erfüllt daher die Bewegungsgleichung (Herleitung siehe Lagrange-Formalismus)
gehen, stationär. Die physikalisch tatsächlich durchlaufene Bahn erfüllt daher die Bewegungsgleichung (Herleitung siehe Lagrange-Formalismus)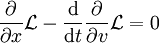 .
.
Bei Bewegung eines Teilchens im Potential ist dies die Newtonsche Bewegungsgleichung
Differentialgleichungen, die sich derart aus einem Wirkungsfunktional durch Variation ableiten lassen, nennt man variationell selbstadjungiert. Alle elementaren Feld- und Bewegungsgleichungen der Physik sind variationell selbstadjungiert.
Symmetrie
Man sagt, dass eine Differentialgleichung eine Symmetrie besitzt, wenn es eine Transformation des Raumes der Kurven gibt, die die Lösungen der Differentialgleichungen auf Lösungen abbildet. Für variationell selbstadjungierte Differentialgleichungen erhält man eine solche Transformation, wenn die Transformation das Wirkungsfunktional bis auf Randterme invariant lässt. Das Noether-Theorem besagt, dass die Invarianz des Wirkungsfunktionals gegenüber einer einparametrigen stetigen Transformationsgruppe die Existenz einer Erhaltungsgröße zur Folge hat und dass umgekehrt jede Erhaltungsgröße die Existenz einer (mindestens infinitesimalen) Symmetrie der Wirkung zur Folge hat.
Wir beschränken uns hier auf Symmetrien in der klassischen Mechanik. Für den feldtheoretischen Beweis verweisen wir auf die englische Version des Artikels.
Sei Φs eine einparametrige, differenzierbare Gruppe von Transformationen, die (genügend differenzierbare) Kurven
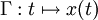 auf Kurven
auf Kurven 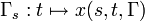 abbildet und gehöre der Parameterwert s = 0 zur identischen Abbildung,
abbildet und gehöre der Parameterwert s = 0 zur identischen Abbildung, 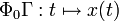 .
.Beispielsweise bildet ΦsΓ = Γs mit
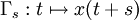 jede Kurve Γ auf die um s früher durchlaufene Kurve ab. Die Transformation ΦsΓ = Γs mit
jede Kurve Γ auf die um s früher durchlaufene Kurve ab. Die Transformation ΦsΓ = Γs mit 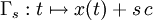 verschiebt jede Kurve um eine Konstante
verschiebt jede Kurve um eine Konstante 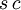 .
.Die Transformationen Φs heißen lokal, wenn sich die Ableitung bei der identischen Abbildung, die infinitesimale Transformation
für alle Kurven Γ als Funktion δx(t,x,v) der Zeit, des Ortes x und der Geschwindigkeit v, ausgewertet auf der Kurve Γ, schreiben lässt,
Beispielsweise sind die Verschiebungen von Zeit und Ort lokal und gehören zur infinitesimalen Transformation δx = v beziehungsweise zu
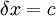 .
.Ist nun
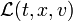 die Lagrangefunktion des mechanischen Systems. Dann heißen die lokalen Transformationen Φs Symmetrien der Wirkung, wenn sich für alle Kurven Γ die Lagrangefunktion bei infinitesimalen Transformationen nur um die Zeitableitung einer Funktion K(t,x), ausgewertet auf Γ, ändert,
die Lagrangefunktion des mechanischen Systems. Dann heißen die lokalen Transformationen Φs Symmetrien der Wirkung, wenn sich für alle Kurven Γ die Lagrangefunktion bei infinitesimalen Transformationen nur um die Zeitableitung einer Funktion K(t,x), ausgewertet auf Γ, ändert,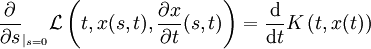 .
.
Denn dann ändert sich die Wirkung nur um Randterme
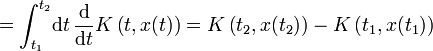 .
.
Der Zusammenhang dieser Definition der Symmetrie der Wirkung mit der Erhaltungsgröße wird klar, wenn man die partiellen Ableitungen der Lagrangefunktion nach s ausführt, und dabei als Kurzschrift die Definition der infinitesimalen Transformation verwendet
Ergänzt man den ersten Term zu einem Vielfachen der Bewegungsgleichung und zieht man die Ergänzung beim zweiten Term ab, entsteht
und die Definitionsgleichung einer infinitesimalen Symmetrie einer Wirkung lautet
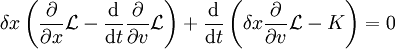 .
.
Da aber das δx-fache der Bewegungsgleichungen auf den physikalisch durchlaufenen Bahnen verschwindet, besagt diese Gleichung, dass die Funktion
die zur Symmetrie gehörige Noetherladung, sich auf den physikalisch durchlaufenen Bahnen nicht ändert,
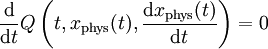 .
.
Umgekehrt ist jede Erhaltungsgröße definitionsgemäß eine Funktion Q(t,x,v), deren Zeitableitung auf physikalischen Bahnen verschwindet, also ein Vielfaches (von Ableitungen) der Bewegungsgleichungen ist. Dieses Vielfache definiert die infinitesimale Symmetrie
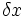 .
.Anmerkungen
- Symmetrien der Bewegungsgleichungen sind nicht immer Symmetrien der Wirkung. Beispielsweise ist die Streckung
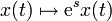 eine Symmetrie der Bewegungsgleichung
eine Symmetrie der Bewegungsgleichung 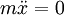 des freien Teilchens, nicht aber eine Symmetrie seiner Wirkung mit der Lagrangefunktion
des freien Teilchens, nicht aber eine Symmetrie seiner Wirkung mit der Lagrangefunktion 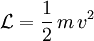 . Zu solch einer Symmetrie der Bewegungsgleichungen gehört keine Erhaltungsgröße.
. Zu solch einer Symmetrie der Bewegungsgleichungen gehört keine Erhaltungsgröße.
- Die zu einer Symmetrie gehörige Erhaltungsgröße als Funktion der Zeit, des Ortes und der Geschwindigkeiten verschwindet genau dann, wenn es sich um eine Eichsymmetrie handelt. In solch einem Fall sind die Bewegungsgleichungen nicht unabhängig, sondern eine Bewegungsgleichung gilt als Folge der anderen. Dies besagt das zweite Noethertheorem.
- Das Noethertheorem erklärt, warum man bei Multiplikation der Newtonschen Bewegungsgleichungen mit den Geschwindigkeiten bei zeitunabhängigem Potential den Energieerhaltungssatz erhält: die Geschwindigkeit ist die infinitesimale Änderung des Ortes bei zeitlicher Verschiebung. Ebenso erklärt das Noethertheorem, warum bei drehinvariantem Potential das Produkt der Bewegungsgleichungen mit dem Kreuzprodukt
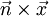 auf die Erhaltung des Drehimpulses in Richtung
auf die Erhaltung des Drehimpulses in Richtung 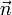 führt: das Kreuzprodukt
führt: das Kreuzprodukt 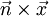 ist die infinitesimale Änderung von x bei Drehung um die Achse
ist die infinitesimale Änderung von x bei Drehung um die Achse 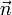 .
.
- Bei Verschiebungen und Drehungen des Ortes ist die Lagrangefunktion strikt invariant, das heißt, die Funktion K verschwindet. Das gilt aber nicht für zeitliche Verschiebung und bei Transformation auf ein gleichmäßig bewegtes Bezugssystem. Unter zeitlichen Verschiebungen ist die Wirkung invariant, wenn die Lagrangefunktion nur vom Ort x und der Geschwindigkeit v, nicht aber von der Zeit abhängt. Dann ändert sich die Lagrangefunktion unter zeitlichen Verschiebungen um
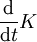 mit
mit 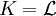 . Die zugehörige Erhaltungsgröße ist definitionsgemäß die Energie
. Die zugehörige Erhaltungsgröße ist definitionsgemäß die Energie
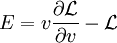 .
.
Ist bekannt, wie die Energie von der Geschwindigkeit abhängt, so legt diese Gleichung die Lagrangefunktion bis auf einen Anteil fest, der linear in den Geschwindigkeiten ist und nicht zur Energie beiträgt. Denn zerlegt man die Lagrangefunktion beispielsweise in Anteile
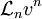 , die homogen vom Grad n in der Geschwindigkeit sind, dann tragen sie mit
, die homogen vom Grad n in der Geschwindigkeit sind, dann tragen sie mit 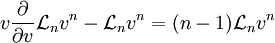 zur Energie bei. Ist also
zur Energie bei. Ist also 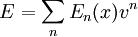 , so ist die Lagrangefunktion
, so ist die Lagrangefunktion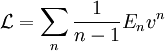 .
.
Insbesondere besteht in Newtonscher Physik die Energie aus der kinetischen Energie, die quadratisch in der Geschwindigkeit ist, n = 2, und der geschwindigkeitsunabhängigen potentiellen Energie, n = 0. Daher ist die Lagrangefunktion 1 / (2 − 1)-mal die kinetische Energie plus 1 / (0 − 1)-mal potentielle Energie. In der relativistischen Physik sind in Maßsystemen mit c = 1 die Lagrangefunktion und die Energie eines freien Teilchens der Masse m
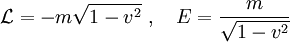 .
.
Siehe auch
Literatur
- Noether, E.: Invarianten beliebiger Differentialausdrücke. Gött. Nachr. 1918, 37-44 (1918). Zusammenfassung im Zentralblatt MATH
- Noether, E.: Invariante Variationsprobleme. Gött. Nachr. 1918, 235-257 (1918). Zusammenfassung im Zentralblatt MATH
-
Wikimedia Foundation.

![W[\Gamma]=\int_{t_1}^{t_2}\!\mathcal{L} \left( t,x(t),
\frac{\mathrm{d}x}{\mathrm{d}t} \right)\,\mathrm{d}t](/pictures/dewiki/48/041e9e059b34f49f9adee1295179bd40.png)
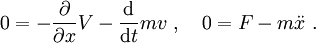
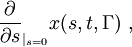
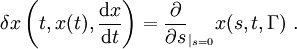
![\frac{\mathrm{d}}{\mathrm{d}s}W[\Gamma_s]_{|_{s=0}}=
\int_{t_1}^{t_2}\!\mathrm{d}t\,
\frac{\partial}{\partial s}_{|_{s=0}}
\mathcal{L} \left(t, x(s,t), \frac{\partial x}{\partial
t}(s,t) \right)](/pictures/dewiki/101/e6e7a95f9e2ce63c2e2f35d7b89d6239.png)