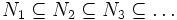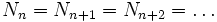Noethersch

In der Algebra werden bestimmte Strukturen (Ringe und Moduln) noethersch genannt, wenn sie keine unendliche Schachtelung von immer größeren Unterstrukturen enthalten können. Der Begriff ist nach der Mathematikerin Emmy Noether benannt.

Noethersche Moduln

Es sei R ein unitärer Ring (d. h. ein Ring mit Einselement). Ein R-Linksmodul M heißt noethersch, wenn er eine der folgenden äquivalenten Bedingungen erfüllt:^[1]

• Jeder Untermodul ist endlich erzeugt.
• (Aufsteigende Kettenbedingung) Jede unendliche aufsteigende Kette

$N_1 \subseteq N_2 \subseteq N_3 \subseteq\ldots$

von Untermoduln wird stationär, d.h. es gibt einen Index n, so dass

$N_n = N_{n+1} = N_{n+2} = \ldots$

• (Maximalbedingung für Untermoduln) Jede nichtleere Menge von R-Untermoduln von M hat ein maximales Element bezüglich Inklusion.

Noethersche Ringe

Ein Ring R heißt

• linksnoethersch, wenn er als R-Linksmodul noethersch ist;
• rechtsnoethersch, wenn er als R-Rechtsmodul noethersch ist;
• noethersch, wenn er links- und rechtsnoethersch ist.

Bei kommutativen Ringen sind alle drei Begriffe identisch und äquivalent dazu, dass alle Ideale in R endlich erzeugt sind.

Eigenschaften und Beispiele

• Ist R linksnoethersch, das Jacobson-Radikal 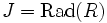$J=\operatorname{Rad}(R)$ nilpotent, und R / J halbeinfach, dann ist R auch linksartinsch.
• Endlich erzeugte Moduln über noetherschen Ringen sind noethersch. Die endlich erzeugten Moduln über einem noetherschen Ring bilden eine abelsche Kategorie; die Voraussetzung, dass der Ring noethersch ist, ist dabei essentiell.
• Quotienten und Lokalisierungen noetherscher Ringe sind noethersch.
• Ist R ein noetherscher Ring, so ist auch der Polynomring R[X] noethersch (Hilbertscher Basissatz).
• Daraus folgt, dass allgemein endlich erzeugte Algebren über einem noetherschen Ring wieder noethersch sind. Insbesondere sind endlich erzeugte Algebren über Körpern noethersch.
• Hauptidealringe oder allgemeiner Dedekindringe sind noethersch.
• Der Polynomring $\Bbb C[X_1, X_2, ...]$ in unendlich vielen Unbestimmten ist nicht noethersch, da das Ideal, das von allen Unbestimmten erzeugt wird, nicht endlich erzeugt ist.
• Der Matrizenring 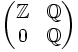$\begin{pmatrix} \Z & \mathbb{Q} \\ 0 & \mathbb{Q} \end{pmatrix}$ ist rechtsnoethersch, aber weder linksartinsch noch linksnoethersch.
• Ist M ein R-Linksmodul und 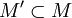$M' \subset M$ ein Untermodul, so ist M noethersch genau dann, wenn sowohl M' als auch M/M' noethersch sind. ^[2]

Siehe auch

• artinsch

Einzelnachweise

1. ↑ Beweis dazu
2. ↑ Beweis dazu

Literatur

• Bourbaki, N.,Eléments de mathématique. Algèbre commutative. Chapitre 8: Dimension. Chapitre 9: Anneaux locaux noethériens complets. (French) Paris etc.: Masson. 200 p. FF 150.00 (1983)
• David Eisenbud: Commutative Algebra with a View Toward Algebraic Geometry. Springer-Verlag, New York, Berlin, Heidelberg, London, Paris, Tokyo, Hong Kong, Barcelona 1999, ISBN 978-0-387-94269-8 (engl.)