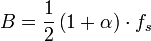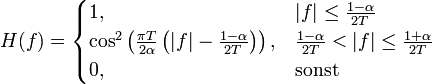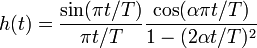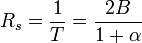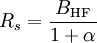Nyquist-Filter

Das Raised-Cosine-Filter, auch als Kosinus-Roll-off-Filter oder Nyquist-Filter bezeichnet, ist ein in der digitalen Signalverarbeitung, einem Teilbereich der Nachrichtentechnik, angewandtes elektronisches Filter welches zur Formung von Signalimpulsen verwendet wird.

Als wesentliche Eigenschaft erfüllt dieses Filter die erste Nyquistbedingung. Dies bedeutet, dass zeitlich aufeinanderfolgende Signalimpulse welche mit diesem Filter geformt werden sich nicht gegenseitig überlagern und beeinträchtigen. Damit erlaubt dieses Filter eine zeitlich diskrete Signalübertragung in welcher keine Intersymbolinterferenz (ISI) auftritt.

Darstellung

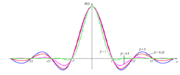
Ein Raised-Cosine-Filter weist immer die Eigenschaften eines Tiefpasses auf und wird in digitalen Filterstrukturen wie ein Filter mit endlicher Impulsantwort (FIR) realisiert. Seine Übertragungsfunktion, der Betrag des Frequenzganges, ist bis zu einer bestimmten Frequenz, welche von einem Roll-off-Faktor abhängt, konstant und fällt darüber hinaus für höhere Frequenzen kosinusförmig bis auf den Wert Null ab. Aus diesem Umstand leitet sich auch die Bezeichnung dieses Filters ab.

Das Raised-Cosine-Filter wird bei digitalen Signalübertragungen zur Formung jener am Übertragungskanal verwendeten Sendeimpulse verwendet. Die Sendeimpulse, oder auch Symbole genannt, stellen die diskrete, zu übertragene Information dar. Der Übertragungskanal kann beispielsweise ein Funkkanal oder auch leitungsgebunden sein. Anwendungen liegen daher bei digitalen Übertragungen wie beispielsweise im Mobilfunkbereich.

Die Implementierung jenes Filters erfolgt in digitalen Signalprozessoren (DSP), anwendungsspezifischen digitalen Schaltungen (ASIC) oder frei programmierbaren digitalen Schaltungen, den so genannten Field Programmable Gate Arrays (FPGA).

Übertragungsfunktion

Die Übertragungsfunktion dieses Filters ist, abgesehen von der bei zeitdiskreten Übertragungssystemen immer wesentlichen Symbolrate (1/T), von einem speziellen Faktor, dem Roll-off-Faktor α abhängig. Die Bezeichnung α für den Roll-off-Faktor ist in der Literatur nicht einheitlich gewählt. Es kommen auch Bezeichnungen wie r oder β vor.

Mit diesem Faktor, welcher Werte zwischen 0 und 1 annehmen kann, wird die Steilheit der Übertragungskennlinie wesentlich beeinflusst: Für den Grenzwert α = 0 ergibt sich ein idealer, nicht kausaler Tiefpass mit rechteckförmiger Übertragungsfunktion. Für α = 1 ergibt sich die bei diesem Filtertyp eine maximal flache Kosinusflanke. Für Zwischenwerte ist der bezogene Frequenzgang einen bestimmten Bereich annähernd konstant, und fällt erst ab dann mit einer etwas steilern Kosinusflanke ab, wie in nachfolgenden Abbildungen dargestellt:

Betragsverlauf der Übertragungsfunktion mit unterschiedlichen Roll-off-Faktoren β

Impulsantwort mit unterschiedlichen Roll-off-Faktoren β

Je größer der Roll-off-Faktor ist, desto mehr nimmt die Bandbreite des Filters zu. Die Bandbreite kann aufgrund der zeitdiskreten Eigenschaft, nur maximal bis zur Symbolrate 1/T zunehmen. Ein kleinerer Roll-off-Faktor verringert die Bandbreite zwar nur unwesentlich, aber die steile Filterflanke führt zu größeren unerwünschten Überschwingungen, die letztlich in realen Übertragungsystemen ein grösseres Phasenrauschen und damit eine unzureichende Pulsformung bewirken und zu Fehlern in der Demodulation führen können.

In der Praxis wird meist ein Roll-off-Faktor unter 0,5 im Bereich von 0,2 bis 0,5 verwendet. So verwendet beispielsweise der Mobilfunkstandard UMTS für die darin verwendeten Impulsfilter einen Roll-off-Faktor von α = 0,22.

Die Bandbreite des Filters mit der Symbolrate f_s = 1/T berechnet sich zu:

$B=\frac{1}{2}\left(1+\alpha\right)\cdot f_s$

Mathematische Beschreibung der Übertragungsfunktion

Die auf 1 normierte Übertragungsfunktion H(f) ist gegeben durch:

$H(f)=\begin{cases} 1, & |f| \leq \frac{1-\alpha}{2T} \\ \cos^2\left(\frac{\pi T}{2 \alpha}\left( |f| - \frac{1 - \alpha}{2 T}\right)\right), & \frac{1-\alpha}{2T} < |f| \leq \frac{1+\alpha}{2T} \\ 0, & \textrm{sonst} \end{cases}$

mit der Impulsantwort h(t):

$h(t) = \frac{\sin(\pi t/T)}{\pi t/T} \frac{\cos (\alpha \pi t/T)}{1 - (2 \alpha t/T)^2}$

Dabei ist ersichtlich, dass das Filter einen Verlauf der si-Funktion aufweist, welche bei den Vielfachen der Symboldauer T Nullstellen hat und damit Intersymbolfreiheit garantiert.

Symbolrate

Die übertragbare Symbolrate eines Raised-Cosine-Filters bei gegebenen Roll-off-Faktors α und einer Bandbreite B beträgt:

$R_s=\frac{1}{T}=\frac{2B}{1+\alpha}$

Da im Bandpassbereich die doppelte Bandbreite zur Verfügung steht ergibt sich:

$R_s=\frac{B_{\mathrm{HF}}}{1+\alpha}$

Im Bandpassbereich liegt die Bandbreiteneffizienz im Grenzfall von α=0 bei 2 Symbole/s pro Hertz Bandbreite bzw. bei binärer Übertragung 2 Bit/s pro Hertz Bandbreite. Bei praktischen Realisierungen werden Roll-off-Faktoren im Bereich α=0,3 (30%) gewählt, wodurch sich bei binärer Übertragung eine spektrale Effizienz von ca. 1,5 Bit/s pro Hertz Bandbreite ergibt.

Augendiagramm

Die folgenden Abbildungen zeigen Augendiagramme von Raised-Cosine-Filtern mit verschiedenen Roll-off-Faktoren. Mit diesem lässt sich die Qualität der Signale beurteilen.

Roll-off-Faktor 0 (idealer Tiefpass)

Roll-off-Faktor 0,25

Root-Raised-Cosine-Filter

Das Root-Raised-Cosine-Filter, kurz RRC, entspricht der Wurzel (engl. root) aus dem Raised-Cosine-Filter.

Siehe auch

• Adjacent Channel Power

Literatur

• John B. Anderson: Digital Transmission Engineering. 2. Auflage. Wiley Interscience, Lund, Schweden 2005, ISBN 0-471-69464-9. 

Weblinks

• gute Informationen über passive Filter (PDF; 544 KB)
• Information über RC- und RRC-Filter
• Beispiel Raised-Cosine-Filter 7. Ordnung
• Monolithisch integrierte Empfängerschaltung (PDF, 3,3 MB)
• Grundlagen der digitalen Modulation (PDF; 1,1 MB)