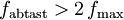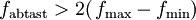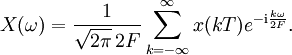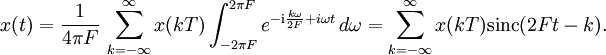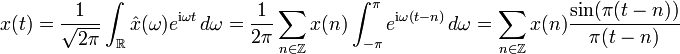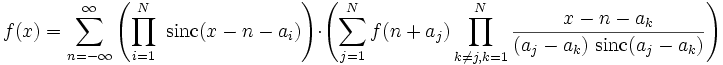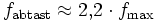Nyquist-Shannon-Theorem

Das Nyquist-Shannonsche Abtasttheorem, in neuerer Literatur auch WKS-Abtasttheorem (für Whittaker-Kotelnikow-Shannon) genannt, ist ein grundlegendes Theorem der Nachrichtentechnik, Signalverarbeitung und Informationstheorie. Claude Elwood Shannon formulierte es 1948 als Ausgangspunkt seiner Theorie der maximalen Kanalkapazität, d. h. der maximalen Bitrate in einem frequenzbeschränkten, rauschbelasteten Übertragungskanal ^[1].

Das Abtasttheorem besagt, dass ein kontinuierliches, bandbegrenztes Signal, mit einer Minimalfrequenz von 0 Hz und einer Maximalfrequenz f_max, mit einer Frequenz größer als 2 · f_max abgetastet werden muss, damit man aus dem so erhaltenen zeitdiskreten Signal das Ursprungssignal ohne Informationsverlust (aber mit unendlich großem Aufwand) exakt rekonstruieren und (mit endlichem Aufwand) beliebig genau approximieren kann.

Geschichtliche Entwicklung

Claude Shannon stützte sich auf Überlegungen von Harry Nyquist zur Übertragung endlicher Zahlenfolgen mittels trigonometrischer Polynome und auf die Theorie der Kardinalfunktionen von Edmund Taylor Whittaker (1915) und dessen Sohn John Macnaughten Whittaker (1929) ^[2].

Unabhängig davon wurde das Abtasttheorem 1933 von Wladimir Alexandrowitsch Kotelnikow ^[3] in der sowjetischen Literatur eingeführt, was im Westen allerdings erst in den 1950er Jahren bekannt wurde. Ansätze zur Interpolation mittels Kardinalreihen oder ähnlicher Formeln lassen sich bis in die Mitte des 19. Jahrhunderts zurückverfolgen.

Zuerst bewiesen wurde das Abtasttheorem im Jahre 1939 von Herbert P. Raabe (1909-2004).^[4]

Motivation

Für Nicht-Basisband-Signale, die eine minimale Frequenz f_min größer 0 Hz haben, gilt das Abtasttheorem in einer verallgemeinerten Form; die Abtastfrequenz muss dann größer als zweimal die Bandbreite (= zweimal die Differenz zwischen oberer und unterer Grenzfrequenz) des Signals sein (siehe Abschnitt Unterabtastung).

Im Zuge der Abtastung entsteht eine Impulsamplitudenmodulation. Bei jeder Form der Amplitudenmodulation, die sich durch die Multiplikation der Signale bestimmen lässt, entstehen neben dem Träger zwei Seitenbänder, deren Breite sich nach der Bandbreite des modulierenden Signals richtet. Wegen dieser zwei Seitenbänder entsteht der Faktor 2 im Abtasttheorem. Tastet man das Eingangssignal mit zu geringer Frequenz ab, dann verringert sich der Abstand der periodischen Spektren im Frequenzbereich, die aus der periodischen Abtastung entstehen. Diese Spektren besitzen jeweils diese erwähnten Seitenbänder, die sich damit zu überlappen beginnen. Überlappende Frequenzspektren lassen sich nicht mehr trennen und damit kann auch das Originalsignal nicht mehr hergestellt werden.

Im Spezialfall einer unteren Grenzfrequenz gleich 0 wird also

$f_{\rm abtast} > 2\,f_{\rm max}$

gefordert, im allgemeinen Fall

$f_{\rm abtast} > 2(\,f_{\rm max} - f_{\rm min})$

In der Praxis bedeutet das Abtasttheorem, dass man vor der Abtastung die maximale Frequenz kennen oder herausfinden muss (zum Beispiel mit Hilfe der Fourier-Analyse eines hochfrequent abgetasteten Signals) und dass dann das Signal (zum Beispiel zum Zwecke der Digitalisierung) mit mehr als der doppelten Frequenz abgetastet werden muss, wenn man das Signal in guter Näherung rekonstruieren will.

Das Nyquist-Shannon-Abtasttheorem findet bei jeder Digitalisierung Anwendung. 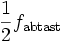$\frac{1}{2} f_{\rm abtast}$ nennt man, nach Vorschlag von C. E. Shannon, die Nyquist-Frequenz.

Analog gilt das Abtasttheorem auch bei Bildern, wobei die Abtastfrequenz dann in Linien (bzw. Pixel) pro Längeneinheit bestimmt werden kann.

Erklärung der Begriffe

• Ein bandbeschränktes Signal x mit einer maximalen Frequenz F:=f_max ist eine Funktion, für welche die Fouriertransformierte 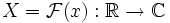$X=\mathcal F(x):\R\to\mathbb C$ existiert und diese Fouriertransformierte außerhalb des Intervalls [ − 2πF,2πF] Null ist. Dann kann umgekehrt das bandbeschränkte Signal durch die inverse Fouriertransformation der Frequenzdichte dargestellt werden:

$x(t)=\frac1{\sqrt{2\pi}}\int_{-2\pi F}^{2\pi F} X(\omega)e^{\mathrm{i}\omega\,t}\, d\omega$.

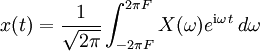„Gute“, zulässige Funktionen für die Frequenzdichte X sind beispielsweise stückweise stetige Funktionen, für die in jedem Punkt beide der einseitigen Grenzwerte existieren. Allgemeiner sind Funktionen aus dem Funktionenraum $L^2([-2\pi F,2\pi F],\mathbb C)$ zulässig.

Ist x reellwertig, so gilt 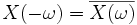$X(-\omega)=\overline{X(\omega)}$. Wird X in Polarkoordinaten dargestellt, 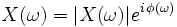$X(\omega)=|X(\omega)|e^{i\,\phi(\omega)}$, so erhalten wir x mittels eines Integrals mit reellem Integranden,

$x(t)=\sqrt{\frac2\pi}\int_0^{2\pi F}|X(\omega)|\,\cos(\omega\,t+\phi(\omega))\, d\omega$.

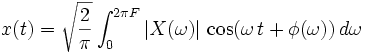In der kartesischen Darstellung X(ω) = A(ω) + iB(ω) ergibt sich analog

$x(t)=\sqrt{\frac2\pi}\int_0^{2\pi F}\left(A(\omega)\,\cos(\omega\,t)-B(\omega)\,\sin(\omega\,t)\right)\, d\omega$.

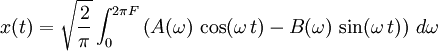• Abtasten mit der doppelten Frequenz bedeutet hier, dass Funktionswerte in gleichmäßigen Abständen genommen werden, wobei ein einfacher Abstand T = 1/(2 F) beträgt, d. h. aus x wird die Zahlenfolge x[k]:=x(kT) konstruiert. Nach der Fourierdarstellung ergeben sich diese Werte aus der Frequenzdichte als

$x(kT)=\frac1{\sqrt{2\pi}}\int_{-2\pi F}^{2\pi F} X(\omega)e^{\mathrm{i}\frac{k\omega}{2F}}\, d\omega$.

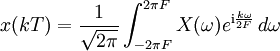Diese sind aber gerade die Koeffizienten in der Fourierreihenentwicklung

$X(\omega)=\frac1{\sqrt{2\pi}\,2F}\sum_{k=-\infty}^\infty x(kT) e^{-\mathrm{i}\frac{k\omega}{2F}}.$

Somit ist die Frequenzdichte und damit das Signal schon durch die Werte der Abtastfolge vollständig determiniert.

• Rekonstruieren ohne Informationsverlust bedeutet, dass die Lagrange-Interpolation, ausgeweitet auf den Fall mit unendlich vielen, regelmäßig angeordneten Stützstellen, wieder das Ausgangssignal ergibt

$x(t)=y(t):=\sum_{k=-\infty}^\infty x_k\prod_{j\in\mathbb Z,\;j\ne k}\frac{t-jT}{kT-jT} =\sum_{k=-\infty}^\infty x(kT)\ \mathrm{sinc}(t/T-k)$.

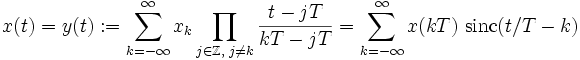Man beachte, dass zur Bestimmung eines jeden Signalwertes eine Summation über einen unendlichen Bereich notwendig ist. Außerdem müssen unendlich viele Takte abgewartet werden, bevor die Summation abgeschlossen werden kann.

Die Funktion 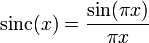$\operatorname{sinc}(x) = \frac{\sin(\pi x)}{\pi x}$, der Sinus cardinalis, ist dabei der ideale Interpolationskern für ganzzahlige Stützstellen; es ist sinc(0)=1 und sinc(n)=0 für jedes weitere ganzzahlige n. Die interpolierende Reihe wird auch, nach Whittakers Notation, als Kardinalreihe bezeichnet, dabei bezieht sich die Vorsilbe kardinal auf die herausragende Rolle als „schwankungsärmste“ unter allen interpolierenden Funktionenreihen. Die sinc-Funktion hat, bis auf einen Faktor, die Rechteck-Funktion 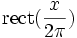$\operatorname{rect}(\frac{x}{2\pi})$ als Fourier-Transformierte, diese hat den Wert 1 auf dem Intervall [ − π;π], sonst den Wert Null. Sie ist also bandbeschränkt mit höchster Frequenz 1/2.

Die Entwicklung als Kardinalreihe ergibt sich nun ganz natürlich, indem die Fourierreihe der Frequenzdichte in die inverse Fouriertransformation eingesetzt wird,

$x(t)=\frac1{4\pi F}\,\sum_{k=-\infty}^\infty x(kT) \int_{-2\pi F}^{2\pi F} e^{-\mathrm{i}\frac{k\omega}{2F}+i\omega t}\,d\omega =\sum_{k=-\infty}^\infty x(kT) \operatorname{sinc}(2Ft-k).$

• Ein reelles Nicht-Basisband-Signal muss, um Abtastung durch Funktionswerte zu erlauben, eine nur für Frequenzen aus dem Intervall [2πnF,2π(n + 1)F] nicht verschwindende Fourier-Transformierte haben. Dann ist F die einseitige Bandbreite. Dieses kann auf Frequenzbänder beliebigen Zuschnitts verallgemeinert werden, allerdings ist dann das Abtasten nicht durch Funktionswerte, sondern durch Skalarprodukte zu definieren. Ein Beispiel dafür ist das Frequenzmultiplexverfahren, siehe auch OFDM.

Bemerkung: Kein endliches Signal, d. h. keine Funktion mit einem endlichen Träger erfüllt die Voraussetzungen an eine bandbeschränkte Funktion. Ebenso wenig fallen periodische Signale, wie zum Beispiel reine Sinusschwingungen, in den Bereich dieses Theorems; genauso wenig Signale mit Knicken oder Sprüngen. Es ist somit als ideale Aussage in einer idealen Situation zu betrachten. Dem Ideal am nächsten kommen modulierte Schwingungen, wie Musik- oder Sprachaufzeichnungen, die zum Speichern auf CD gesampelt und digitalisiert werden sollen. Für andere praktische Zwecke, zum Beispiel digitale Bildbearbeitung, müssen Varianten des Abtasttheorems mit nicht ganz so starken Anforderungen gefunden werden, für die dieses Theorem dann Richtschnur ist. Siehe Quelle: M. Unser: Sampling…

Tiefpass zur Verhinderung von Signalstörungen

Eventuell enthaltene Signalanteile mit einer Frequenz größer der halben Abtastfrequenz müssen vor der Abtastung mit einem (analogen) Tiefpass-Filter aus dem Signal entfernt werden, da es sonst zu Artefakten kommt. Die Entfernung dieser Anteile führt zu einer Veränderung des Signals und sollte nur angewendet werden, wenn diese Änderung unwesentlich ist oder eine Erhöhung der Abtastfrequenz nicht in Frage kommt. Die Artefakte sind Alias-Signale (Störsignale, Pseudosignale), die sich als störende Frequenzanteile bemerkbar machen. Wird zum Beispiel ein Sinussignal, das eine Frequenz von 1600 Hz hat, mit einer Abtastfrequenz von 2000 Hz digitalisiert, erhält man ein 400 Hz Alias-Signal (2000 bis 1600 Hz). Bei einer Abtastfrequenz über 3200 Hz entsteht dagegen kein Alias-Signal. Eine Abtastfrequenz von zum Beispiel 3300 Hz führt zu einem Differenzsignal von 1700 Hz (3300 bis 1600 Hz). Dieses ist jedoch größer als die halbe Abtastrate und wird demnach bei der Rekonstruktion durch einen Tiefpass entfernt.

Mathematischer Hintergrund

Zu mathematischen Grundlagen siehe: Lebesgue-Integral, Lebesgue-Raum, Fourier-Transformation

Durch Skalieren der Zeitabhängigkeit kann jedes bandbeschränkte Signal x(t) auf den Frequenzbereich [-½; ½], bzw. [-π; π] als Kreisfrequenzbereich, reduziert werden. Die Frequenzdichte g(f) muss eine Funktion beschränkter Variation sein, wie es zum Beispiel stückweise stetige Funktionen sind. Dann ist x(t) eine stetige, beliebig oft differenzierbare, absolut- und quadratintegrable Funktion, 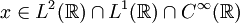$x\in L^2(\R)\cap L^1(\R)\cap C^\infty(\R)$, und hat eine Fourier-Transformierte 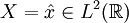$X=\hat x\in L^2(\R)$ mit Träger $\mbox{supp}\,\hat x\subset [-\pi,\pi]$.

Der Funktionswert x(t) an jedem beliebigen Punkt t ist unter diesen Voraussetzungen schon allein durch die Funktionswerte x(n) an allen ganzzahligen Punkten t=n festgelegt, es gilt:

$x(t)=\sum_{n=-\infty}^\infty x(n)\cdot \frac{\sin(\pi(t-n))}{\pi(t-n)} =\frac{\sin(\pi t)}{\pi}\sum_{n=-\infty}^\infty\frac{(-1)^n x(n)}{t-n}$.

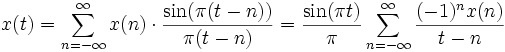Diese Gleichung enthält zwei nichttriviale Aussagen: 1) Die unendliche Reihe konvergiert, und 2) der Grenzwert ist immer identisch mit dem Funktionswert x(t).

Die Identität einer bandbeschränkten Funktion mit ihrer oben angegebenen Kardinal-Reihe (nach Whittaker) ergibt sich aus der Poissonschen Summenformel, es gilt 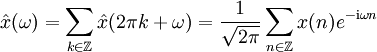$\hat x(\omega)=\sum_{k\in\mathbb Z} \hat x(2\pi k+\omega)=\frac1{\sqrt{2\pi}}\sum_{n\in\mathbb Z} x(n)e^{-\mathrm{i}\omega n}$, woraus sich nach der Formel der Inversen Fourier-Transformation $x(t)=\frac1{\sqrt{2\pi}}\int_{\mathbb R}\hat x(\omega)e^{\mathrm{i}\omega t}\,d\omega =\frac1{2\pi}\sum_{n\in\mathbb Z}x(n)\int_{-\pi}^\pi e^{\mathrm{i}\omega(t-n)}\,d\omega =\sum_{n\in\mathbb Z}x(n)\frac{\sin(\pi(t-n))}{\pi(t-n)}$ Durch geschickte Anwendung der allgemeinen Abtastformel kann man auch verallgemeinerte Kardinalreihenentwicklungen erhalten, zum Beispiel 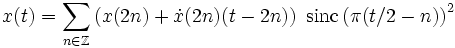$x(t)=\sum_{n\in\mathbb Z}\left(x(2n)+\dot x(2n)(t-2n)\right)\ \mathrm{sinc}\left(\pi(t/2-n)\right)^2$, d. h. die Abtastrate ist halbiert, dafür werden an jedem Abtastpunkt zwei Werte genommen, der Funktionswert und die erste Ableitung. Es wird gewissermaßen lokal linear entwickelt und die Entwicklungen mittels einer Zerlegung der Eins „zusammengeklebt“. Formeln mit Ableitungen höherer Ordnung erlauben keine so einfache Interpretation. (Siehe [Higgins: Five. ..]) Ist f bandbeschränkt auf Kreisfrequenzen aus dem Intervall [-Nπ; Nπ] und sind a1,…,aN paarweise verschiedene reelle Zahlen, so gilt $f(x)=\sum_{n=-\infty}^\infty \left(\prod_{i=1}^N\ \mathrm{sinc}(x-n-a_i)\right)\cdot\left( \sum_{j=1}^N f(n+a_j)\prod_{k\ne j,k=1}^N\frac{x-n-a_k}{(a_j-a_k)\ \mathrm{sinc}(a_j-a_k)}\right)$ Der erste Faktor im Summanden ist die Kernfunktion einer Zerlegung der Eins, der zweite Faktor ein Interpolationspolynom, das der Lagrange-Interpolation ähnlich sieht. Lässt man die ak simultan nach 0 laufen und ersetzt f(n + ak) durch das Taylor-Polynom vom Grad N-1 oder größer, so ergeben sich beliebig komplexe differentielle Kardinalreihen.

Artefakte

Wird die Abtastfrequenz unbedacht zu klein gewählt, treten Artefakte auf. Diese nicht linearen Verzerrungen sind auch unter dem Begriff Alias-Effekt bekannt. Im Bild treten phasenverschobene Schatten oder neue Strukturen auf, die im Original nicht enthalten sind.

Beispiel Bilder

Alias-Signale treten auch beim Scannen von Vorlagen mit wechselnden Ortsfrequenzen auf, man spricht dann von einem Moiré-Effekt; zum Beispiel Kleidungsstücke wie Wollpullis oder Anzüge mit dünnen Streifen, auch Ziegeldächer usw. Oft sind Moirés auch im Fernsehen zu sehen, wenn Moderatoren Nadelstreifenanzüge tragen.

Im hier vorliegenden Fall ist die Ursache eine Überlagerung der Spektren der Abtast-Funktion, deren Ausgangssignale mit f_abtast periodisch sind.

Beispiel Töne

Das erste Klangbeispiel lässt einen Ton erklingen, dessen Frequenz von ca. 100 Hz bis über 8000 Hz linear zunimmt (die Original-Abtastfrequenz von 16 kHz wurde bei der Transformation in das Ogg-Vorbis Format auf 42 kHz heraufgesetzt). Das zweite Beispiel gibt fast das gleiche Signal wieder, dieses Mal mit 8000 Hz abgetastet. Durch Unterabtastung werden Töne oberhalb von 4000 Hz falsch ausgelesen mit dem Ergebnis, dass eine Tonhöhe aufgezeichnet wird, die abfällt, statt zu steigen.

Linear ansteigender Ton (16 kHz Abtastung)

Linear ansteigender Ton (8 kHz Abtastung)

Modifizierte Formel für praktische Anwendung

In der Praxis gibt es (prinzipiell aus Gründen der Kausalität) keinen idealen Tiefpass. Er hat immer einen gewissen Übergangsbereich zwischen praktisch keiner Dämpfung im Durchlassbereich und praktisch vollständiger Dämpfung im Sperrbereich. Daher verwendet man in der Praxis eine modifizierte Formel:

Beispiel:

$f_{\rm abtast} \approx 2{,}2 \cdot f_{\rm max}$

Bei einer CD werden Frequenzen bis 20 kHz übertragen, die Abtastfrequenz beträgt 44,1 kHz.

Der verwendete Faktor ist abhängig vom verwendeten Tiefpassfilter und von der benötigten Dämpfung der Alias-Signale. Andere gebräuchliche Faktoren sind 2,4 (DAT, DVD) und 2,56 (FFT-Analysatoren)

Überabtastung

Wenn man eine höhere Abtastfrequenz wählt, erhält man keine zusätzlichen Informationen. Der Aufwand für Verarbeitung, Speicherung und Übertragung steigt jedoch. Trotzdem wird Überabtastung (oversampling) häufig angewendet. Liegt nämlich die Nutzbandbreite B sehr nahe bei der halben Abtastfrequenz, so werden sehr hohe Anforderungen an die Flankensteilheit des Tiefpassfilters gestellt. Diese analogen Filter können häufig nur mit großem Aufwand abgeglichen werden.

Überabtastung erlaubt es, die Anforderungen an das analoge Tiefpassfilter drastisch zu reduzieren, indem die steilflankige Bandbegrenzung auf ein präzises Digitalfilter hoher Ordnung verlagert wird. In der Praxis wird häufig ein Überabtastungsfaktor M = 2 oder M = 4 gewählt. Somit braucht man weniger steile analoge Filter vor dem Abtasten. Nach der Abtastung wird dann ein digitales Filter zur Abtastratenreduktion eingesetzt, welches gleichzeitig die Abtastfrequenz reduziert. Dieses digitale Filter wird auch als Dezimationsfilter bezeichnet und kann beispielsweise in Form eines Cascaded-Integrator-Comb Filters realisiert werden.

Mathematisch ausgedrückt hat ein idealer Tiefpassfilter als Übertragungsfunktion eine Rechteckfunktion. Diese Übertragungsfunktion schneidet das Spektrum im Frequenzraum perfekt ab, und das gefilterte Signal kann perfekt aus den Abtastpunkten rekonstruiert werden. Allerdings lässt sich ein idealer Tiefpassfilter nicht praktisch realisieren, da er nicht kausal und unstetig ist.

Deswegen verwendet man ein analoges Tiefpassfilter welche eine stetige, trapezähnliche Übertragungsfunktion aufweisen und deren Flanken mit kontinuierlicher, endlicher Steigung zu- bzw. abnehmen. Diese Filter können beispielsweise in Form von Butterworth-Filtern realisiert werden. Nach dem Abtasten erfolgt die digitale Glättung auf die Nutzbandbreite und das Heruntertakten. Die Flankensteilheit hat dabei einen Einfluss auf die Güte des rekonstruierten Signals.

Unterabtastung (Sub-Nyquist-Sampling)

Das Konzept f_abtast > 2 · f_max ist eine vereinfachte Darstellung, die allerdings sehr gebräuchlich und nützlich ist. Genau genommen muss anstelle von f_max die Bandbreite stehen, die durch den Bereich zwischen niedrigster und höchster im Signal vorkommenden Frequenz definiert ist. Nur in Basisbandsignalen ist die Bandbreite mit f_max identisch, Basisbandsignale sind Signale mit niederfrequenten Anteilen in der Nähe von 0 Hz.

Diese Erkenntnis führte zu einem Konzept namens Unterabtastung, das zum Beispiel in digitaler Radiotechnik Verwendung findet. Angenommen, man möchte alle Radiosender empfangen, die zwischen 88 und 108 MHz senden. Interpretiert man das Abtasttheorem wie bisher beschrieben, so müsste die Abtastfrequenz über 216 MHz liegen. Tatsächlich wird aber durch die Technik der Unterabtastung nur eine Abtastfrequenz von etwas mehr als 40 MHz benötigt. Voraussetzung dafür ist, dass vor der Abtastung aus dem Signal mittels Bandpassfilter alle Frequenzen außerhalb des Frequenzbereichs von 88 bis 108 MHz entfernt werden. Die Abtastung erfolgt beispielsweise mit 44 MHz, ohne dass der relevante Bereich von einem analogen Mischer umgesetzt würde – das Ergebnis ist quasi ein Alias-Signal und entspricht dem Signal, das bei Abtastung eines per Mischer auf 0–22 MHz umgesetzten Bereichs entstünde.

Um in der Praxis die notwendige punktförmige Abtastung wenigstens näherungsweise realisieren zu können, muss die Abtast-Halte-Schaltung jedoch derart ausgelegt werden, dass das Ausleseintervall so eng wird, wie es für eine Abtastfrequenz von 220 MHz oder mehr vonnöten wäre. Zu vergleichen ist das mit einer Abtastung mit 220 MHz, von der nur jeder fünfte Wert weiterbenutzt wird, während die je vier dazwischenliegenden Abtastwerte verworfen werden.

Kausalität

In der Signaltheorie ist ein System kausal, wenn das Ausgangssignal nicht vor Beginn des Eingangssignals erscheint. Alle physikalisch realisierbaren Systeme sind demnach kausal.

Einzelnachweise

1. ↑ Claude Elwood Shannon: Communication in the Presence of Noise; In: Proc. IRE, Vol. 37, No. 1 (Jan. 1949), Nachdruck in: Proc. IEEE, Vol. 86, No. 2, (Feb. 1998)
2. ↑ J. M. Whittaker: The Fourier theory of the cardinal functions, Proc. Edinburgh Math. Soc. 1 (1929)
3. ↑ Wladimir A. Kotelnikow: On the transmission capacity of „ether“ and wire in electrocommunications, Izd. Red. Upr. Svyazzi RKKA, 1933
4. ↑ Hans Dieter Lüke: The Origins of the Sampling Theorem, IEEE Communications Magazine, S. 106–108, April 1999. Online-Version

Literatur

• Harry Nyquist: Certain Topics in Telegraph Transmission Theory. Trans. Amer. Inst. Elect. Eng. 47, Nachdruck in: Proc. IEEE, Vol. 90, No. 2, 1928, Nachdruck 2002, S. 617 bis 644 (http://www.loe.ee.upatras.gr/Comes/Notes/Nyquist.pdf). 
• J. R. Higgins: Five short stories about the cardinal series. Bulletin of the AMS 12, 1985. 
• Michael Unser: Sampling-50 Years after Shannon. (http://bigwww.epfl.ch/publications/unser0001.html). 
• Dr.-Ing.W.Wunderlich: Digitales Fernsehen HDTV, HDV, AVCHD für Ein-und Umsteiger. ISBN 978-3-00-023484-2. 

Weblinks

• Demonstrationsprogramm zum Abtasttheorem