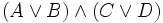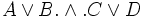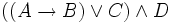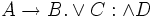Operatorpräzedenz

Als Operatorrangfolge, -wertigkeit, -priorität oder -präzedenz, bezeichnet man in Mathematik, Logik und Informatik eine definierte Halbordnung, in der die Operatoren eines in Infix-Schreibweise vorliegenden Ausdrucks auszuwerten sind.

Die Halbordnung sagt aus, dass es keine strikte Reihenfolge zwischen allen Operatoren gibt, sondern dass mindestens zwei auf demselben Rang sind. Zum Beispiel ist der Rang von Multiplikation und Division gleich, aber höher als der Rang von Addition und Subtraktion („Punktrechnung vor Strichrechnung“). Man kann durch die Rangfolge eine explizite Klammerung sparen. So ist 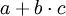$a + b \cdot c$ gleichbedeutend mit 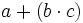$a + (b \cdot c)$, wenn der Multiplikationsoperator einen höheren Rang hat. Dieses ist jedoch immer Definitionssache.

Eine Klammerung bietet in der Regel die Möglichkeit, die vorgegebene Rangfolge punktuell außer Kraft zu setzen. Wenn man 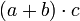$(a + b) \cdot c$ schreibt, wird c erst auf die Summe von a und b angewendet. Eine Reihenfolge ist damit noch nicht gegeben, weil der Ausdruck sowohl von links nach rechts als auch von rechts nach links (oder beliebig) ausgewertet werden kann. Das hängt von der jeweiligen Definition ab.

Rangfolge unterschiedlicher Operatoren

Für die Standard-Rechenoperationen der Mathematik ist (in absteigender Priorität) folgende Rangfolge üblich:

1. Potenzierung
2. Multiplikation und Division („Punktrechnung“)
3. Addition und Subtraktion („Strichrechnung“)

In Programmiersprachen und Computerprogrammen zur Formelauswertung (z. B. dem Unix-Dienstprogramm bc) gibt es zusätzliche Kategorien. Eine davon ist das Vorzeichen, das in der Regel eine noch höhere Priorität vor der Potenzierung genießt. So wird in mathematischen Formeln der Ausdruck − a^b zwar als − (a^b) gelesen, in den Ausdrücken solcher Auswertungsprogramme aber oft als ( − a)^b.

In der Logik ist es nicht immer üblich, eine Operatorrangfolge zu definieren. Wo das geschieht, wird meistens (in absteigender Priorität) folgende gewählt:

1. Negation
2. Konjunktion
3. Disjunktion
4. Konditional
5. Bikonditional

Nach Anwendung der genannten Operatorrangfolgen wird z. B. der arithmetische Ausdruck 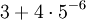$3+4 \cdot 5^{-6}$ ausgewertet als 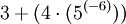$3+(4\cdot(5^{(-6)}))$, der logische Ausdruck 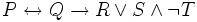$P \leftrightarrow Q \rightarrow R \or S \and \neg T$ als $P \leftrightarrow (Q \rightarrow (R \or (S \and (\neg T))))$.

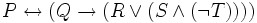Reihenfolge gleichwertiger Operatoren

Zusätzlich kann für Operationen eine Assoziativität festgelegt werden, mit der bestimmt wird, in welcher Reihenfolge nebeneinander stehende, gleichwertige Operatoren auszuwerten sind. Ein Operator heißt linksassoziativ, wenn A op B op C op D ausgewertet wird als ((A op B) op C) op D; ein Operator heißt rechtsassoziativ, wenn A op B op C op D ausgewertet wird als A op (B op (C op D)). Von den genannten arithmetischen Operatoren wird die Potenzierung als rechtsassoziativ definiert, d. h.:

$a^{b^{c^{d}}} \ = \ a^{\left(b^{\left(c^{d}\right)} \right)}\ \neq \ \left(\left(a^b\right)^c\right)^d$.

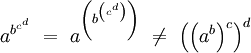Die übrigen zweistelligen Operatoren werden als linksassoziativ definiert, d. h. zum Beispiel A − B − C − D = ((A − B) − C) − D.

In der Logik werden Junktoren meistens linksassoziativ definiert, es gibt aber durchaus auch Autoren, die zumindest das Konditional rechtsassoziativ verwenden.

Es gibt auch Programmiersprachen, wie z. B. Occam, die alle Operatoren auf dem gleichen Rang setzen und von links nach rechts auswerten.

Gliederungszeichen

Um innerhalb eines Ausdrucks die definierte Operatorrangfolge zu verändern bzw. um bei fehlender Definition einer Rangfolge Ausdrücke eindeutig zu gestalten werden unterschiedliche Formen von Gliederungszeichen verwendet. In der Mathematik und auch in der modernen Logik sind das Klammern.

In der Geschichte der Logik wurden vor allem zu Beginn häufig Punktierungen verwendet, um Ausdrücke zu disambiguieren bzw. eine allenfalls definierte Operatorrangfolge zu verändern. Ein Punktierungssystem, das durch das Grundlagenwerk Principia Mathematica eine gewisse Verbreitung erlangte, war bis in die 1970-er-Jahre in unterschiedlich abgewandelter Form auch in einführenden Logikbüchern häufiger anzutreffen. Bei diesem System wird statt der gedachten schließenden Klammer vor einem Junktor bzw. statt der gedachten öffnenden Klammer nach einem Junktor ein Punkt gesetzt. Zum Beispiel würde statt

$(A \or B) \and (C \or D)$

der folgende Ausdruck geschrieben:

$A \or B. \and .C \or D$

Treffen mehrere gedachte Klammern aufeinander, dann werden statt eines einzigen Punktes zwei oder mehrere Punkte gesetzt, sodass zum Beispiel anstelle von

$((A \rightarrow B) \or C) \and D$

der folgende Ausdruck geschrieben würde:

$A \rightarrow B. \or C: \and D$

Ein anderes System gewichtet die in einem Ausdruck vorkommenden Junktoren mit Punkten. Je mehr Punkte über einem Operator stehen, desto schwächer ist seine Bindungsstärke, d. h. desto niedriger ist seine Priorität. Nach diesem System würde zum Beispiel eine Konjunktion mit zwei Punkten schwächer binden als eine Konjunktion mit einem Punkt, diese wiederum schwächer als eine Konjunktion ohne Punkte.

Sonstiges

In Programmiersprachen wird meist eine Wertigkeit und Assoziativität für alle Operatoren festgelegt, damit die Struktur aller Ausdrücke auch dann eindeutig ist, wenn keine Klammern verwendet werden. Damit erfolgt bei der Auswertung des Ausdrucks stets denselben Wert.

Die Operatorrangfolge ist normalerweise nur bei Ausdrücken in Infix-Notation von Bedeutung. Schreibweisen wie die Polnische Notation oder die Umgekehrte Polnische Notation wurden entwickelt, damit die Ausdrücke ohne Rangfolge und klammerfrei eindeutig sind. Auch bei der ersten prädikatenlogischen Schreibweise, der Begriffsschriftnotation und bei graphischen Schreibweisen wie den Existential Graphs ist die Lesart eines Ausdrucks eindeutig bestimmt und bedarf keiner Gliederungszeichen oder -konventionen.

Literatur

• Florian Cajori: A History of Mathematical Notations. Open Court, Chicago 1928–1929, Dover, New York 1993. ISBN 0-486-67766-4
• William Kneale, Martha Kneale: The Development of Logic. Clarendon Press, Oxford 1962. ISBN 0-19-824773-7