Overfitting

blau: Fehler bzgl. Trainingsdatensätzen
rot: Fehler bzgl. Testdatensätzen
Wenn der Fehler bzgl. der Testdatensätze steigt, während der Fehler bzgl. der Trainingsdatensätze stetig fällt, dann befindet man sich möglicherweise in einer Überanpassungssituation.

Überanpassung (engl. overfitting) bezeichnet eine bestimmte Korrektur eines Modells an einen vorgegebenen Datensatz. In der Statistik bedeutet Overfitting die Spezifizierung eines Modells in der multiplen Regressionsanalyse, das zu viele erklärende Variablen enthält.

Mathematische Definition

Gegeben sei ein Hypothesenraum H und eine Hypothese 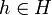$h \in H$. Dann wird h überangepasst an die Trainingsdaten genannt, wenn es eine alternative Hypothese 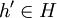$h' \in H$ gibt, so dass h einen kleineren Fehler gegenüber h' auf den Trainingsdaten aufweist, aber h' einen kleineren Fehler als h in Bezug auf die Verteilung aller Instanzen hat.

Statistik

In der multiplen Regression wird mit overfitting ein Modell charakterisiert, das zusätzliche, irrelevante Regressoren (erklärende Variablen) enthält. Werden dagegen relevante Variablen außer Acht gelassen, spricht man von underfitting.^[1]
Durch die Aufnahme zusätzlicher Regressoren kann das Bestimmtheitsmaß R², das die Güte der Anpassung des Modells an die Daten der Stichprobe misst, nicht sinken. Durch Zufallseffekte können so irrelevante Regressoren zur Erklärung der Varianz beitragen und das Bestimmtheitsmaß künstlich erhöhen.
Overfitting ist als negativ zu beurteilen, weil also die tatsächliche (geringere) Anpassungsgüte verschleiert wird und das Modell zwar besser auf die Daten der Stichprobe angepasst wird, allerdings keine Übertragbarkeit auf die Grundgesamtheit besteht. Regressionskoeffizienten erscheinen fälschlicherweise als nicht signifikant, da ihre Wirkung nicht mehr hinreichend genau geschätzt werden kann. Die Schätzer sind ineffizient, d.h. ihre Varianz ist nicht mehr minimal. Gleichzeitig wächst die Gefahr, dass irrelevante Variablen aufgrund von Zufallseffekten als statistisch signifikant erscheinen.^[2] Overfitting verschlechtert so die Schätzeigenschaften des Modells, insbesondere auch dadurch, dass eine zunehmende Anzahl von Regressoren die Zahl der Freiheitsgrade verringert.^[3] Große Unterschiede zwischen R² und dem korrigierten Bestimmtheitsmaß deuten auf overfitting hin. Overfitting kann v.a. durch sachlogische Überlegungen und die Anwendung einer Faktorenanalyse entgegengewirkt werden.

Datensätze und überangepasste Modelle

Zunächst ist die Auswahl des Datensatzes, insbesondere die Zahl von Beobachtungen, Messpunkten oder Stichproben, ein wesentliches Kriterium für eine seriöse und erfolgreiche Modellbildung. Sonst erlauben die aus diesen Daten gewonnenen Annahmen überhaupt keine Rückschlüsse auf die Wirklichkeit. Dies gilt auch insbesondere für statistische Aussagen.

Anders ausgedrückt: Wer versucht, in vorhandenen Daten nach Regeln oder Trends zu suchen, der muss geeignete Daten wählen. Wer eine Aussage über die häufigsten Buchstaben des deutschen Alphabets treffen möchte, sollte dafür nicht nur einen einzelnen Satz betrachten, zumal wenn in diesem der Buchstabe „E“ selten vorkommt.

Überanpassung durch zu viel Training

Bei der rechnergestützten Modellbildung kommt ein zweiter Effekt hinzu. Hier wird in mehreren Trainingschritten ein Datenmodell an vorhandene Trainingsdaten angepasst. Beispielsweise kann mit einigen dutzend Schriftproben ein Rechner trainiert werden, dass er handgeschriebene Ziffern (0–9) richtig erkennt und zuordnet. Das Ziel ist hierbei, auch Handschriften von Personen erkennen zu können, deren Handschrift gar nicht in dem Trainingssatz enthalten war.

Folgende Erfahrung wird häufig gemacht: die Erkennungsleistung für geschriebene Ziffern (unbekannter Personen) mit zunehmender Anzahl der Trainingsschritte nimmt zunächst zu. Nach einer Sättigungsphase nimmt sie aber wieder ab, weil sich die Datenrepräsentation des Rechners zu sehr an die Schreibweise der Trainingsdaten anpasst und nicht mehr an den zugrundeliegenden Formen der zu lernenden Ziffern selbst orientiert. Dieser Prozess hat den Begriff Überanpassung im Kern geprägt, auch wenn der Zustand der Überangepasstheit wie oben beschrieben, eine Reihe von Gründen haben kann.

Wenn mit dem Modell kein Einsatz über die Trainingsmenge hinaus geplant ist, wenn also nur ein Modell für eine abgeschlossene Problemstellung gelöst wird, kann natürlich von Überanpassung nicht die Rede sein. Ein Beispiel hierfür wäre, wenn nur ein Rechnermodell für die abgeschlossene Menge von Vorfahrtsituationen im Straßenverkehr gesucht wird. Solche Modelle sind deutlich weniger komplex als das oben genannte und meistens kennt man die Regeln schon, so dass von Menschen verfasste Programme hier meist effizienter sind, als maschinelles Lernen.

Beispiele

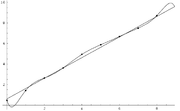Verrauschte (ungefähr lineare) Daten lassen sich sowohl durch eine lineare als auch durch eine polynomielle Funktion beschreiben. Obwohl die polynomielle Funktion durch jeden Datenpunkt geht, anders als die lineare, beschreibt die lineare Funktion den Verlauf besser, da sie keine größeren Abweichungen an den Enden hat. Wenn die Regressionskurve zum Extrapolieren der Daten benutzt würde, wäre die Überanpassung noch größer.

Eine militärische Bilderkennungssoftware mit dem Zweck, getarnte Panzer auf Fotos zu erkennen, funktionierte im Training tadellos, mit neuen Testfotos aber nicht mehr. Der Grund: Die Trainingsfotos mit Panzern waren bei einem anderen Sonnenstand aufgenommen worden als die ohne Panzer; die Software hatte dem eigentlich irrelevanten Sonnenstand eine übermäßige Bedeutung beigemessen.

Literatur

• Michael Berthold, David J. Hand: Intelligent Data Analysis: An Introduction. Springer Verlag, 2003, ISBN 3-540-43060-1
• Tom M. Mitchell: Machine Learning. McGraw-Hill Companies, Inc., 1997, ISBN 0-07-115467-1

Einzelnachweise

1. ↑ Backhaus, K., Erichson, B., Plinke, W., Weiber, R.: Multivariate Analysemethoden. Eine anwendungsorientierte Einführung. Berlin u.a., 11. Auflage 2006, S.84-85.
2. ↑ Backhaus, K., Erichson, B., Plinke, W., Weiber, R.: Multivariate Analysemethoden. Eine anwendungsorientierte Einführung. Berlin u.a., 11. Auflage 2006, S.85.
3. ↑ Backhaus, K., Erichson, B., Plinke, W., Weiber, R.: Multivariate Analysemethoden. Eine anwendungsorientierte Einführung. Berlin u.a., 11. Auflage 2006, S.68.