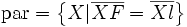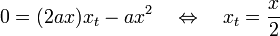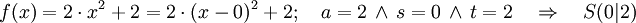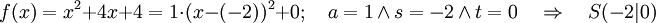Parabolisch

Ein hüpfender Ball beschreibt, wenn man den Reibungsverlust vernachlässigt, Parabelbögen.

In der Mathematik ist eine Parabel zweiter Ordnung (v. griech.: παραβολή parabole = das Daneben-Geworfene"; der Vergleich, v. altgriech.: paraballein = nebenhin werfen, nebeneinanderstellen) eine Kurve, genauer ein Kegelschnitt, der entsteht, wenn man den Kegel mit einer Ebene schneidet, die parallel zu einer Mantellinie des Kegels ist. Wenn die Ebene selbst eine Tangentialebene des Kegels ist, erhält man eine Gerade als degenerierte Parabel 2. Ordnung oder Parabel der Ordnung 1.

Allgemein werden unter Parabeln die Funktionsgraphen von ganzrationalen Funktionen verstanden. Hat die Funktion den Grad n, dann wird der Graph als Parabel der Ordnung n bezeichnet. Die oben genannten Kegelschnitte lassen sich bis auf den erwähnten Spezialfall als Graphen von quadratischen Funktionen also Funktionen der Form 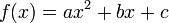$f(x)=ax^2+bx+c\$ darstellen.

In geometrischen Untersuchungen werden manchmal unter Parabeln nur Parabeln zweiter Ordnung verstanden. Die besonderen Eigenschaften der Parabeln zweiter Ordnung werden im Folgenden genauer beschrieben.

Darstellungsformen

Eine Parabel

Neben der oben genannten Definition als Kegelschnitt kann eine Parabel auch als Punktmenge in einem kartesischen Koordinatensystem beschrieben werden:

Eine Parabel ist die Menge aller Punkte X, deren Abstand zu einem speziellen festen Punkt - dem Brennpunkt F - und einer speziellen Geraden - der Leitgeraden l - gleich ist.

$\operatorname{par} = \left\{X |\overline{XF} = \overline{Xl}\right\}$

Der Punkt, der in der Mitte zwischen Brennpunkt und Leitgerade liegt, heißt Scheitel A der Parabel. Die Verbindungsgerade von Brennpunkt und Scheitel wird auch Achse der Parabel genannt. Sie ist die einzige Symmetrieachse der Parabel.

Zur Herleitung der algebraischen Bestimmungsgleichung der Parabel wird im Folgenden ein kartesisches Koordinatensystem so festgelegt, dass A die Koordinate (0,0) und F die Koordinate (0,f) besitzt (s. Bild rechts). Für jeden Punkt P(x,y) auf der Parabel gilt damit 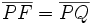$\overline{PF}=\overline{PQ}$, wobei Q der Fußpunkt von P auf der Leitgeraden ist. Dies gilt auch für A, d. h. 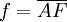$f=\overline{AF}$ ist gleich dem Abstand von A zur Leitgeraden l und es ergibt sich für die Koordinaten x,y der folgende implizite Zusammenhang:

$\sqrt{(y-f)^2+x^2}=y+f$.

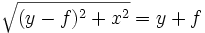Durch Vereinfachung folgt daraus der direkte funktionale Zusammenhang für alle Punkte P(x,y):

$y=x^2 \frac{1}{4f}$.

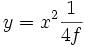Jede quadratische Funktion der Form y = ax² ist somit eine Parabel mit dem Brennpunkt $F\left(0,\tfrac{1}{4a}\right)$.

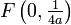Eigenschaften

Koeffizienten

Parabelschablone

Da die Parabel nur von einem Parameter abhängig ist (dem Abstand 2f von Leitgerade und Brennpunkt bzw. dem Parameter a in der obigen Gleichung), sind alle Parabeln zueinander ähnlich. Die Unterschiede in der Krümmung entstehen nur durch das Vergrößerungsverhältnis. Insbesondere ist die numerische Exzentrizität ε = 1 und die lineare Exzentrizität ist gleich der Brennweite 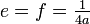$e = f = \tfrac 1{4a}$. Für a = 1, d. h. 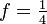$f = \tfrac 14$, spricht man auch von einer Grundparabel oder Normalparabel mit der Koordinatengleichung y = x².

Parabeln können als Grenzfall einer Ellipse oder einer Hyperbel angesehen werden, wenn ein Brennpunkt fix ist und der andere unendlich weit in die eine oder andere Richtung entfernt wird.

Brennpunkt

Wird ein Strahl, der parallel zur Achse einfällt, an der Parabel beziehungsweise an ihrer Tangente gespiegelt, so geht der resultierende Strahl durch den Brennpunkt, und umgekehrt. Dieser resultierende Strahl wird auch Brennlinie, Leitstrahl, oder Brennstrahl des Punktes genannt. Diese Eigenschaft hat auch ein Rotationsparaboloid, also die Fläche, die entsteht, wenn man eine Parabel um ihre Achse dreht; sie wird häufig in der Technik verwendet (siehe Parabolspiegel).

Beweis

Die Steigung der Tangente an die Parabel y = ax² im Punkt P(x,y) ergibt sich zu m = 2ax. Die Nullstellen der Tangenten t erhält man mit Hilfe der allgemeinen Geradengleichung t:y_t = mx_t + l. Für die Tangente durch einen beliebigen Punkt P(x,ax²) der Parabel gilt l = y_t − mx_t = ax² − (2ax)x = − ax² und damit für die Tangentengleichung t:y_t = (2ax)x_t − ax².

Die Nullstelle G(g,0) der Tangente (für 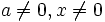$a\not\neq{}0, x\not\neq{}0$) lautet somit:

$0 = (2ax)x_t - ax^2 \quad \Leftrightarrow \quad x_t = \frac{x}{2}$

Also der Punkt 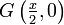$G\left(\tfrac{x}{2},0\right)$. Dieser liegt also genau in der Mitte zwischen F und Q(x, − f). Damit wird das gleichschenklige Dreieck ΔFPQ in zwei kongruente Dreiecke zerlegt. Die Reflexion an der Parabel entspricht der Reflexion an der Tangente.

Der Einfallswinkel 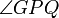$\angle GPQ$ ist gleich dem Ausfallswinkel 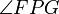$\angle FPG$. Damit treffen alle Strahlen auf F.

Jedes Teilchen, das sich in einem gleichförmigen Gravitationsfeld ohne Einwirkung anderer Kräfte bewegt (zum Beispiel ein Baseball, wenn man den Luftwiderstand ignoriert), folgt einer parabelförmigen Bahn (Wurfparabel). In radialsymmetrischen Gravitationsfeldern, wie sie idealerweise um einen Himmelskörper herrschen, ist die Parabel eine der Lösungen einer Keplerbahn.

Lagebeziehungen

Eine Parabel heißt in Hauptlage, wenn ihr Scheitelpunkt im Koordinatenursprung liegt und ihre Achse mit einer Koordinatenachse zusammenfällt. In der 1. Hauptlage ist die Parabel nach rechts offen; die Achse der Parabel fällt mit der positiven x-Achse zusammen. In 2. Hauptlage befindet sich die Parabel, wenn sie nach oben offen ist bzw. ihre Achse mit der positiven y-Achse zusammenfällt. Analog dazu sind 3. Hauptlage (nach links offen) und 4. Hauptlage (nach unten offen) definiert.

In 2. und 4. Hauptlage kann eine Parabel als mathematische Funktion mit der Funktionsgleichung y = ax² aufgefasst werden. In 1. und 3. Hauptlage wird die Parabel durch eine Gleichung der Form y² = ax beschrieben. Dies ist keine Funktionsgleichung, da jedem x-Wert 2 Funktionswerte entsprechen. Um die Parabel in 1. bzw. 3. Hauptlage als Funktion aufzufassen, muss sie jeweils in den über bzw. unter der x-Achse liegenden Ast getrennt werden. Für die 1. Hauptlage sind diese Funktionen dann 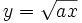$y = \sqrt{ax}$ bzw. $y = -\sqrt{ax}$.

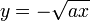Scheitelform

Die Scheitelform oder Scheitelpunktform ist in der Mathematik eine spezielle Darstellung der Parabelfunktion. Mit ihr kann man den tiefsten bzw. höchsten Punkt einer Parabel ablesen.

Die Scheitelpunktfunktion in der allgemeinen Form: 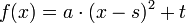$f(x) = a \cdot (x - s)^2 + t$. Der Scheitelpunkt hat dann die Koordinaten S(s | t).

Das Extremum

Anhand der Scheitelpunktform kann man direkt die Lage des Scheitelpunktes, also des einzigen Extrempunkts S(s|t) erkennen. f(s) = t gibt damit also den Extremwert an. Beispiel: f(x)= (x-6)² + 8; Scheitelpunkt (6/8)

Stauchung und Streckung

Durch den Koeffizienten a wird die Stauchung bzw. Streckung der Parabel und die Art der Extremstelle ausgedrückt. Die Normalparabel wird durch den Faktor 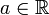$a \in \mathbb{R}$ gestreckt. Daraus ergeben sich die folgenden Möglichkeiten:

a > 1

Streckung bzgl. y-Achse

a = 1

Normalparabel

1 > a > 0

Stauchung bzgl. y-Achse

a = 0

Die Funktion ist keine Parabel sondern eine Konstante (bzw. unendlich stark gestaucht)

0 > a > -1

Stauchung bzgl. y-Achse, Spiegelung bzgl. x-Achse

a = -1

Spiegelung der Normalparabel bzgl. x-Achse

a < -1

Streckung bzgl. y-Achse, Spiegelung bzgl. x-Achse

Beispiele

• $f(x) = 2 \cdot x^2 + 2 = 2 \cdot (x - 0)^2 + 2; \quad a = 2 \, \wedge \, s = 0 \, \wedge \, t=2 \quad \Rightarrow \quad S(0|2)$
• $f(x) = x^2 + 4x + 4 = 1 \cdot (x - (-2))^2 + 0; \quad a = 1 \, \wedge \, s = -2 \, \wedge \, t = 0 \quad \Rightarrow \quad S(-2|0)$

Siehe auch

• Quadratische Funktion
• Paraboloid
• Parabelschablone
• Parabolspiegel
• Parabolantenne
• Wurfparabel

Sonstiges

Genanntes Beispiel

Die Parabel der Funktion f(x) = x² ist eine „Multiplikationsmaschine“. Man kann mit dieser das Ein-mal-Eins berechnen. Dazu muss man zuerst eine Parabel der Form f(x) = x² in einem kartesischen Koordinatensystem einzeichen. Danach die Faktoren der Multiplikation als x-Werte mit zugehörigem y-Wert als Punkt im Koordinatensystem eintragen, wobei das Vorzeichen beider x-Werte nicht dieselben sein dürfen und diese verbinden. Der Schnittpunkt der Geraden mit der y-Achse (Ordinate) ist das Ergebnis der Multiplikation.

Für das Beispiel 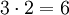$3\cdot 2=6$ trägt man die Faktoren als x-Werte mit unterschiedlichen Vorzeichen in das Koordinatensystem ein. Man wählt also folgende Punkte: P( − 3 | 9), Q(2 | 4) oder P(3 | 9), Q( − 2 | 4).

Verbindet man die Punkte durch eine Gerade, erkennt man, dass der Schnittpunkt der Geraden mit der y-Achse gleich 6 ist.

Weblinks

• Animierte Parabel (Java-Applet erzeugt mit GeoGebra)