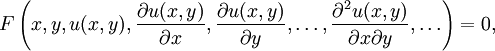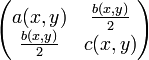PDGL

Eine Partielle Differentialgleichung (Abkürzung PDG oder PDGL, beziehungsweise PDE für engl. partial differential equation) ist eine Differentialgleichung, die partielle Ableitungen enthält. Sie dienen der mathematischen Modellierung vieler physikalischer Vorgänge. Die Lösungstheorie von partiellen Differentialgleichungen ist für lineare Gleichungen weitgehend erforscht, bei nichtlinearen Gleichungen enthält die mathematische Theorie noch viele Lücken. Zur praktischen Berechnung von Lösungen werden in der Regel numerische Verfahren herangezogen.

Definition

Etwas genauer gesagt ist eine PDG eine Gleichung (oder ein Gleichungssystem) für eine oder mehrere unbekannte Funktionen, die folgende Kriterien erfüllt:

• die unbekannte Funktion hängt von mindestens zwei Variablen ab (wenn sie nur von einer Variable abhängt, bezeichnet man sie als gewöhnliche Differentialgleichung, oder kurz nur Differentialgleichung)
• in der PDG kommen partielle Ableitungen nach mindestens 2 Variablen vor
• in der Gleichung kommen nur die Funktion, sowie deren partielle Ableitungen, jeweils am gleichen Punkt ausgewertet vor.

Die implizite Form einer partiellen Differentialgleichung für eine Funktion u, die von zwei Variablen x und y abhängt, lautet

$F\left(x,y,u(x,y),\frac{\partial u(x,y)}{\partial x},\frac{\partial u(x,y)}{\partial y}, \ldots,\frac{\partial^2 u(x,y)}{\partial x \partial y},\ldots \right) = 0,$

wobei F eine beliebige Funktion ist. Im mehrdimensionalen Fall schreibt man auch

$F\left(x,u(x),\operatorname{D} u,\operatorname{D}^2 u, \ldots \operatorname{D}^k u,\ldots \right) = 0,$.

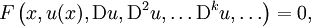Mit den partiellen Ableitungen vom Grad k D^ku.

Gleichungen, in denen neben partiellen Ableitungen auch Integrale auftreten, nennt man Integro-Differentialgleichung.

Beispiel

Viele physikalische Prozesse hängen sowohl vom Ort als auch von der Zeit ab. Die Veränderung bezüglich beider ist nicht immer wichtig: die Bewegung eines Massenpunktes wird nur durch Ableitungen nach der Zeit (Geschwindigkeit und Beschleunigung) beschrieben. So eine Art von Gleichung nennt man gewöhnliche Differentialgleichung. Oft reicht das jedoch nicht aus: Die Wellen, die durch einen Wassertropfen, der auf eine Wasseroberfläche fällt, entstehen, hängen sowohl von der Zeitableitung (Geschwindigkeit der Welle) also auch von der Raumableitung (Profil der Welle) ab. Da Ableitungen nach mehreren Variablen auftauchen, ist also eine partielle Differentialgleichung zur Beschreibung des Vorgangs notwendig.

Das einfachste mögliche Beispiel einer partiellen Differentialgleichung ist folgendes: Eine Funktion u(x,t) möge von 2 Variablen abhängen (z. B. von Ort x und Zeit t). Die partielle Ableitung 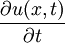$\frac{\partial u(x,t)}{\partial t}$ gibt an, wie stark sich die Funktion in der Zeit ändert, analog gibt 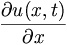$\frac{\partial u(x,t)}{\partial x}$ die Änderung der Funktionswerte in der Ortsvariablen an. Falls diese beiden Änderungen gleich sind, ergibt sich folgende Differentialgleichung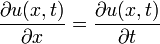

$\frac{\partial u(x,t)}{\partial x} = \frac{\partial u(x,t)}{\partial t}$

Eine Lösung dieser Gleichung wäre u(x,t) = f(x + t) mit einer beliebigen differenzierbaren Funktion f.

Einteilung

Man kann PDGs nach verschiedenen Kriterien einteilen. Den Grad der höchsten Ableitung, der in der Gleichung vorkommt, nennt man die Ordnung. Beispielsweise treten in einer Gleichung erster Ordnung nur partielle erste Ableitungen auf.

Weiter kann nach Linearität eingeteilt werden. Falls die unbekannte Funktion, sowie alle auftretenden Ableitungen linear vorkommen, spricht man von einer linearen partiellen Differentialgleichung. Treten alle Ableitungen von höchster Ordnung linear auf, aber die Funktion und Ableitungen niedriger Ordnung nicht, spricht man von einer semilinearen Gleichung. Hierbei heißt linear, dass die Koeffizientenfunktionen (also a(x,y), b(x,y) und c(x,y) im unteren Beispiel) vor der unbekannten Funktion bzw. Ihrer Ableitungen nur von den Veränderlichen abhängen (und nicht von der Funktion selbst). Hängen die Koeffizientenfunktionen vor der höchsten Ableitung zusätzlich von niedrigeren Ableitungen und der unbekannten Funktion ab, spricht man von einer quasilinearen partiellen Differentialgleichung. Ansonsten spricht man von einer nichtlinearen PDG. Eine nichtlineare partielle Differentialgleichung kann man durch Ausdifferenzieren immer in eine quasilineare Form überführen, in der die höchsten Ableitungen linear auftauchen.

Man unterscheidet weiter zwischen hyperbolischen (z. B. die Wellengleichung), parabolischen (z. B. die Wärmeleitungsgleichung) und elliptischen (z. B. die Poisson-Gleichung) Differentialgleichungen. Anschaulich betrachtet, unterscheiden sich die Typen durch die Art der Ausbreitung von Störungen in der Lösung. Diese Klassifizierung ist allerdings nicht eindeutig, es gibt also partielle Differentialgleichungen, die einen gemischten Charakter haben. Als Beispiel für die Einteilung in elliptisch, parabolisch und hyperbolisch sei eine partielle Differentialgleichung der Ordnung 2 in 2 Variablen herangezogen:

$a(x,y) \frac{\partial^2 u(x,y)}{\partial x^2} + b(x,y) \frac{\partial^2 u(x,y)}{\partial x \partial y} + c(x,y) \frac{\partial^2 u(x,y)}{\partial y^2} + d(x,y) \frac{\partial u(x,y)}{\partial x} + e(x,y) \frac{\partial u(x,y)}{\partial y} + f(u,x,y) = 0$

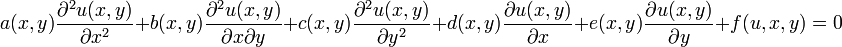
Bei der Einteilung werden immer nur die Koeffizienten der höchsten Ableitungen (hier 2. Ordnung) in der Gleichung betrachtet:

Wenn 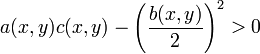$a(x,y) c(x,y) - \left(\frac{b(x,y)}{2}\right)^2 > 0$ ist die Gleichung in (x,y) elliptisch

Wenn 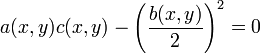$a(x,y) c(x,y) - \left(\frac{b(x,y)}{2}\right)^2 = 0$ ist die Gleichung in (x,y) parabolisch

Wenn 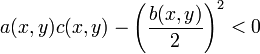$a(x,y) c(x,y) - \left(\frac{b(x,y)}{2}\right)^2 < 0$ ist die Gleichung in (x,y) hyperbolisch

Diese Unterscheidung kann man auch darauf zurückführen, ob die Matrix

$\begin{pmatrix} a(x,y)& \frac{b(x,y)}{2} \\ \frac{b(x,y)}{2}&c(x,y) \end{pmatrix}$

positiv definit (⇒elliptisch), positiv semidefinit, aber nicht definit (singulär) (⇒parabolisch), oder indefinit (mit genau einem negativen Eigenwert) (⇒hyperbolisch) ist. Da a, b und c von x und y abhängen, hängt der Typ der Differentialgleichung vom Ort ab.

Die Typeinteilung für mehr als zwei Variablen erfolgt analog. Im Fall einer Gleichung der Ordnung 2 erstellt man anhand Differentialgleichung eine Matrix A mit den Koeffizientenfunktionen vor partiellen Ableitungen der Ordnung zwei als Einträgen. Die Entscheidung, ob die Gleichung an einer bestimmten Stelle elliptisch, parabolisch oder hyperbolisch ist, erfolgt anhand der Definitheit von A wie im zweidimensionalen Fall. Eventuell muss A mit − 1 multipliziert werden. Für mehr als drei Veränderliche ist die obige Einteilung nicht mehr vollständig, d. h. man kann z. B. im 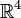$\mathbb{R}^4$ leicht Beispiele konstruieren, die weder elliptisch, parabolisch noch hyperbolisch sind. Dies ist auch bei nichtlinearen Gleichungen so, wo sich der Typ in Raum oder Zeit ändern kann, aber nicht muss.

Rand- und Anfangswertprobleme

Eine partielle Differentialgleichung hat per se im Allgemeinen mehrere Lösungen. Um eine eindeutige Lösung zu erhalten, bedarf es gewisser Zusatzbedingungen, nämlich Rand- und/oder Anfangsbedingungen. Diese Situation ist vergleichbar mit gewöhnlichen Differentialgleichungen, wo man Anfangsbedingungen in einem Punkt braucht. Bei PDGL reicht die Vorgabe eines Funktionswertes an einem Punkt nicht mehr aus. Für eine eindeutige Lösung werden die Funktionswerte (und/oder Ableitungen) auf einer Mannigfaltigkeit benötigt.

Nicht jede Zusatzbedingung führt zu einer vernünftigen Lösung, das Ganze hängt von der Art der Gleichung ab. Typische Beispiele sind

• Dirichlet-Randbedingungen (für elliptische Probleme)
• Neumann-Randbedingungen (für elliptische Probleme)
• schiefe Randbedingungen (für elliptische Probleme)
• Anfangs- und Randbedingungen (für parabolische Probleme)
• Cauchy-Probleme (für hyperbolische Probleme)

Elliptische partielle Differentialgleichungen

Elliptische PDGL treten typischerweise im Zusammenhang mit zeitunabhängigen (stationären) Problemen auf. Ein Kennzeichen ist, dass elliptische Gleichungen oftmals einen Zustand minimaler Energie beschreiben, also aus dem Variationsproblem einer nach unten beschränkten Wirkung herrühren. Die bekanntesten Beispiele sind die Laplace-Gleichung und die Poisson-Gleichung. Diese Gleichungen beschreiben etwa die (stationäre) Temperaturverteilung in einem Körper, oder auch die elektrostatische Ladungsverteilung in einem Körper. Außerdem ist das (Newtonsche) Gravitationspotential eine Lösung der Poisson-Gleichung.

Bei elliptischen Gleichungen sind die am häufigsten auftretenden Randbedingungen entweder Dirichlet-Randbedingungen oder Neumann-Randbedingungen. Die erstere bedeutet, dass die Werte der gesuchten Funktion auf dem Rand vorgegeben sind, während die zweite eine Vorgabe der Normalenableitung der gesuchten Funktion ist. Am Beispiel der Temperaturverteilung soll der Unterschied gezeigt werden: Steckt man ein Objekt in Eiswasser, dann beträgt die Temperatur am Rand 0 Grad Celsius. Damit ist die Temperaturverteilung im Inneren die Lösung eines Dirichlet-Randwertproblems. Ein anderer Fall tritt auf, wenn man den Körper isoliert. Hier ist zwar die Temperatur unbekannt, aber aufgrund der Isolation beträgt der Wärmefluss am Rand 0. Da der Fluss mit der Normalenableitung in Verbindung gebracht werden kann, führt dies auf ein Neumann-Problem. Ähnliches gilt in der Elektrostatik: Kennt man die Spannung die am Rand angelegt wird, kommt man zu einem Dirichlet-Problem, kennt man hingegen die Stromstärke am Rand, erhält man ein Neumann-Problem.

Eine nichtlineare elliptische Gleichung ist die Gleichung für Minimalflächen (Minimal surface equation), die die Form einer Seifenhaut beschreibt, die sich beim Eintauchen eines Drahtgestells in Seifenlauge bildet.

Parabolische partielle Differentialgleichungen

Dieser Typ von Gleichungen beschreibt ähnliche Phänomene wie elliptische Gleichungen, aber im instationären Fall. Das bei weitem wichtigste Beispiel einer parabolischen Gleichung ist die Wärmeleitungsgleichung, die das Abkühlen und Aufheizen eines Körpers beschreibt. Diffusionsprozesse werden ebenfalls durch diese Gleichung beschrieben. Parabolische Gleichungen führen auf ein Anfangs-Randwertproblem. Beispielsweise müssen bei der Wärmeleitungsgleichung am (räumlichen) Rand des Gebietes für alle Zeiten entweder die Temperatur oder der Temperaturfluss vorgegeben werden. Dies entspricht dem Fall von Dirichlet- oder Neumannbedingungen im elliptischen Fall. Zusätzlich muss die Temperaturverteilung am Anfang, also zum Zeitpunkt t = 0 vorgegeben werden. Insgesamt benötigen also parabolische Gleichungen räumliche Randbedingungen und zeitliche Anfangswerte. Ein weiteres, nichtlineares Beispiel einer parabolischen Gleichung ist die Korteweg-de-Vries-Gleichung, die Wasserwellen in Ufernähe beschreibt.

Hyperbolische partielle Differentialgleichungen

Die typische hyperbolische Gleichung ist die Wellengleichung. Allgemein werden durch diese Art von Gleichungen Wellen und deren Ausbreitung beschrieben. Außerdem sind Gleichungen erster Ordnung immer hyperbolisch. Im Unterschied zu parabolischen und elliptischen Gleichung werden Lösungen hyperbolischer Gleichungen wenig bis gar nicht gedämpft. Das führt einerseits zu einer komplizierten Lösungstheorie, da mit weniger Differenzierbarkeit gerechnet werden kann. Andererseits können sich Wellen erst durch diese fehlende Dämpfung über weite Strecken ausbreiten.

Die zu diesem Typ gehörigen Anfangs- und Randwerte führen auf Cauchy-Probleme. Das bedeutet, dass wie im parabolischen Fall zusätzlich zu räumlichen Randbedingungen Anfangswerte benötigt werden. Zur Lösung hyperbolischer Gleichungen zweiter Ordnung benötigt man aber zwei Anfangswerte – den Funktionswert und die zeitliche Ableitung desselben am Anfang. Am Beispiel einer eingespannten Saite soll dies verdeutlicht werden: Die Auslenkung der Saite erfüllt die Wellengleichung. Wenn die Saite an den Enden eingespannt ist, führt dies auf die räumlichen Randbedingungen, in diesem Fall ist die Auslenkung am Rand 0 (weil eingespannt), damit ist der Funktionswert am Rand bekannt und es ergeben sich Dirichlet-Randbedingungen. (Im Fall von frei schwingenden Objekten, wie der Luftsäule in Holzblasinstrumenten, kommt man dementsprechend auf Neumann-Randbedingungen.) Zusätzlich müssen jetzt noch zwei Anfangsbedingungen vorgegeben werden: Die Auslenkung am Anfang (entspricht dem Funktionswert), und die Geschwindigkeit, mit der die Saite am Anfang angezupft wird (entspricht der zeitlichen Ableitung). Mit diesen Bedingungen kann die Auslenkung zu allen späteren Zeitpunkten eindeutig angegeben werden.

Hyperbolische Gleichungen mit paarweise verschiedenen Eigenwerten heißen strikt hyperbolisch. Hier ist die Lösungstheorie auch für nichtlineare Systeme bekannt. Sind die Gleichungen nicht strikt hyperbolisch, wie beispielsweise die mehrdimensionalen Euler-Gleichungen oder die Gleichungen der Magnetohydrodynamik, ist dies nicht mehr der Fall.

Theorie

Folgende Lösungsbegriffe treten bei der Untersuchung von partiellen Differentialgleichungen auf:

• klassische Lösung: Die Lösung ist hinreichend oft differenzierbar.
• starke Lösung: Die Lösung ist im Sinne der schwachen Ableitung hinreichend oft differenzierbar.
• schwache Lösung: Hierbei wird die Gleichung mit einer Testfunktion multipliziert, integriert und dann zumindest teilweise partiell integriert. Eine Lösung dieser neuen Gleichung nennt man schwache Lösung.
• milde Lösung: Starke Lösungen erfüllen häufig eine Form der Variation der Konstanten-Formel. Eine Lösung dieser Formel nennt man milde Lösung. Eine milde Lösung muss jedoch keine starke Lösung sein.

Eine einheitliche Theorie zu partiellen Differentialgleichungen existiert nicht. Im Regelfall müssen die verschiedenen Typen mittels unterschiedlicher Techniken analysiert werden, um Aussagen über Existenz, Eindeutigkeit und weitere Eigenschaften von Lösungen zu erhalten. Lineare partielle Differentialgleichungen sind auch im Fall mehrdimensionaler Systeme hinreichend gut untersucht. Für nichtlineare DGL gilt das nicht.

Wichtige Stichworte sind die greensche Funktion, das Maximumprinzip, der Satz von Cauchy-Kovalevskaja und die Energiemethode von Lions.

• Satz von Holmgren
• Lemma von Lax-Milgram
• Schaudertheorie
• Dirichlet-Prinzip

Numerische Verfahren für partielle Differentialgleichungen

Die meistbenutzten numerischen Verfahren sind die Methode der finiten Elemente (FEM), der finiten Differenzen (FDM) und der finiten Volumina. In den letzten Jahren wird auch verstärkt die Randelement-Methode (REM oder engl. BEM) benutzt.

All diese Verfahren basieren auf einer Diskretisierung der partiellen Differentialgleichung, bei der die Lösung mit Hilfe eines endlichdimensionalen Gebildes approximiert wird.

Literatur

Historische Literatur

• Heinrich Weber: Die partiellen Differential-Gleichungen der mathematischen Physik nach Riemann’s Vorlesungen, Braunschweig: F. Vieweg und sohn, 1900–01.
• Jakob Horn: Einführung in die Theorie der partiellen Differentialgleichungen, Leipzig: G. J. Göschen, 1910.
• Richard Courant und David Hilbert: Methoden der Mathematischen Physik, Zweiter Band, Berlin: J. Springer, 1937.

Modernere Literatur

• Lawrence Craig Evans: Partial Differential Equations. In: Graduate Studies in Mathematics. Band 19, American Mathematical Society, Providence, Rhode Island, 1999, ISBN 0-8218-0772-2.
• D. Gilbarg, N. S. Trudinger: Elliptic Partial Differential Equations of Second Order. In: Grundlehren der mathematischen Wissenschaften. Band 224, Springer-Verlag, Berlin/Heidelberg/New York 1977, ISBN 3-540-08007-4.
• Olga Alexandrowna Ladyschenskaja, Nina N. Uralzewa: Linear and Quasilinear Equations of Elliptic Type. Übersetzt durch L. Ehrenpreis, Academic Press, New York/London 1968, ISBN 0124328504.
• Olga Alexandrowna Ladyschenskaja, W. A. Solonnikow, Nina N. Uralzewa: Linear and Quasi-linear Equations of Parabolic Type. Übersetzt durch S. Smith, American Mathematical Society, Providence, Rhode Island, 1968, ISBN 0821815733.
• Ammon Pazy: Semigroups of Linear Operators and Applications to Partial Differential Equations. In: Applied Mathematical Sciences. Band 44, Springer-Verlag, Berlin 1983, ISBN 3-540-90845-5.