Parakompaktheit

parakompakter Raum

berührt die Spezialgebiete

Mathematik Topologie Analysis

ist Spezialfall von

topologischer Raum

umfasst als Spezialfälle

kompakter Raum parakompakter Hausdorff-Raum metrischer Raum Mannigfaltigkeit

Parakompaktheit ist eine rein topologische Eigenschaft, die einem topologischen Raum zukommt oder nicht und die in sehr vielen mathematischen Aussagen vorausgesetzt wird.

Tatsächlich sind die meisten mathematisch interessanten Räume parakompakte Hausdorff-Räume; dazu gehören insbesondere alle metrischen Räume und Mannigfaltigkeiten. Schwieriger ist es, nicht parakompakte Räume zu finden. Möglicherweise das gängigste Gegenbeispiel ist die sogenannte lange Gerade.

Parakompaktheit ist eine abgeschwächte Form der Kompaktheit; zum Beispiel ist die Menge der reellen Zahlen parakompakt, aber nicht kompakt.

Definition

Ein topologischer Raum M ist parakompakt, falls jede offene Überdeckung eine lokal endliche Verfeinerung besitzt.

Zum Vergleich: Ein topologischer Raum M ist kompakt, falls jede offene Überdeckung eine endliche Teilüberdeckung besitzt.

Dabei bedeutet:

• offene Überdeckung von M: eine Familie $\{U_{i \in I}\}$ von offenen Mengen, deren Vereinigung M ist: $M = \bigcup_{i \in I} U_i$;
• Teilüberdeckung: eine Auswahl $\{U_{j \in J}\}$, deren Vereinigung immer noch M ist;
• Verfeinerung: eine neue Überdeckung 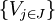$\{V_{j \in J}\}$, wobei jede Menge V_j in mindestens einer Menge U_i der alten Überdeckung enthalten sein muss;
• lokal endlich: zu jedem 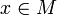$x \in M$ gibt es eine Umgebung, die nur endlich viele Mengen V_j schneidet.