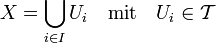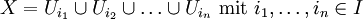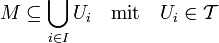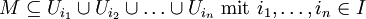- Folgenkompakt
-
kompakter Raum berührt die Spezialgebiete
ist Spezialfall von
umfasst als Spezialfälle
Kompaktheit ist ein zentraler Begriff der mathematischen Topologie, und zwar eine Eigenschaft, die einem topologischen Raum zukommt oder nicht. Sie wird in vielen mathematischen Aussagen vorausgesetzt – oft auch in abgeschwächter Form als Lindelöf-Eigenschaft oder Parakompaktheit. Lokale Kompaktheit ist dagegen eine weder über- noch untergeordnete Bedingung. Eine kompakte Menge nennt man je nach Kontext auch Kompaktum oder kompakter Raum; dabei ist nicht erheblich, ob sie Teilmenge eines Oberraums ist oder nicht.
Einfache Beispiele für kompakte Mengen sind abgeschlossene und beschränkte Teilmengen des Euklidischen Raums
 wie das Intervall [0,1] (bei n=1). Einfache Gegenbeispiele bilden die nicht kompakten Mengen
wie das Intervall [0,1] (bei n=1). Einfache Gegenbeispiele bilden die nicht kompakten Mengen 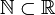 oder
oder 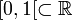 .
.Inhaltsverzeichnis
Definition
Eine Teilmenge des Euklidischen Raums
 heißt kompakt, wenn sie abgeschlossen und beschränkt ist. Für diese spezielle Definition gilt der Satz von Heine-Borel:
heißt kompakt, wenn sie abgeschlossen und beschränkt ist. Für diese spezielle Definition gilt der Satz von Heine-Borel:- Eine Teilmenge des
 ist genau dann kompakt, wenn jede offene Überdeckung der Teilmenge eine endliche Teilüberdeckung enthält.
ist genau dann kompakt, wenn jede offene Überdeckung der Teilmenge eine endliche Teilüberdeckung enthält.
Dies motiviert die folgende, allgemeine Definition der Kompaktheit eines topologischen Raums.
Ein topologischer Raum
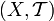 heißt kompakt, wenn jede offene Überdeckung (d. h. Überdeckung durch offene Teilmengen)
heißt kompakt, wenn jede offene Überdeckung (d. h. Überdeckung durch offene Teilmengen)eine endliche Teilüberdeckung
besitzt.
Eine Teilmenge M eines topologischen Raums
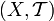 heißt kompakt, wenn jede offene Überdeckung
heißt kompakt, wenn jede offene Überdeckungeine endliche Teilüberdeckung
besitzt.
Die beiden Begriffe sind kompatibel: Eine Teilmenge eines topologischen Raumes ist genau dann kompakt, wenn sie als topologischer Raum mit der Teilraumtopologie kompakt ist.
Einige Autoren wie beispielsweise Boto von Querenburg verwenden für die hier definierte Eigenschaft den Begriff quasikompakt und reservieren den Begriff "kompakt" für kompakte Hausdorff-Räume; dies ist durch die französische Prägung insbesondere in der algebraischen Geometrie üblich.
Beweggrund für die Kompaktheit
Ein wichtiger Grund für die Betrachtung kompakter Räume ist, dass sie in mancher Hinsicht endlichen Mengen ähnlich sind. Anders gesagt gibt es viele Ergebnisse, die sich leicht für endliche Mengen beweisen lassen, deren Beweise aber mit kleinen Änderungen auf kompakte Räume zu übertragen sind. Dies kommt in der Aussage „Kompaktheit ist neben der Endlichkeit die beste Eigenschaft“ zum Ausdruck. Hier ein Beispiel:
Wir setzen voraus, dass X ein Hausdorff-Raum ist und wir einen Punkt x aus X und eine endliche Teilmenge A von X haben, die x nicht enthält. Dann können wir x und A durch Umgebungen trennen: für jedes a aus A seien U(x) und V(a) disjunkte Umgebungen, die jeweils x bzw. a enthalten. Dann sind die Schnittmenge aller U(x) und die Vereinigung aller V(a) die benötigten Umgebungen von x und A.
Ist A nicht endlich, gilt der Beweis nicht mehr, da der Schnitt von unendlich vielen Umgebungen keine Umgebung mehr sein muss. Für den Fall dass A kompakt ist, geht der Beweis allerdings durch, indem man eine endliche Teilüberdeckung der Überdeckung V(a) von A verwendet. Auf diese Weise ist ersichtlich, dass in einem Hausdorff-Raum jeder Punkt durch eine Umgebung von jeder kompakten Menge, in der er nicht enthalten ist, getrennt werden kann. Letztendlich zeigt eine Wiederholung des Beweises, dass zwei beliebige disjunkte kompakte Mengen eines Hausdorff-Raums durch Umgebungen (das heißt durch offene Obermengen) getrennt werden können. Man beachte, dass dies genau das gleiche Ergebnis ist, das man erhält, wenn man „Punkt“ (d. h. einpunktige Menge) durch „kompakte Menge“ im hausdorffschen Trennungsaxiom T2 ersetzt. Viele Beweise und Sätze, die kompakte Räume betreffen, folgen diesem Muster.
Beispiele
Kompakte Räume
- Betrachtet man das geschlossene Einheits-Intervall [0,1] als Teilmenge von
 versehen mit der Standardtopologie, so ist das Intervall ein kompakter, topologischer Raum. Ebenfalls kompakt sind die n-Kugeln und n-1-Sphären betrachtet als Teilmengen der
versehen mit der Standardtopologie, so ist das Intervall ein kompakter, topologischer Raum. Ebenfalls kompakt sind die n-Kugeln und n-1-Sphären betrachtet als Teilmengen der  versehen mit der Standardtopologie für beliebige natürliche Zahlen n.
versehen mit der Standardtopologie für beliebige natürliche Zahlen n. - Alle topologischen Räume mit endlicher Topologie, z. B. endliche Räume, sind kompakt.
- Für eine natürliche Zahl p > 1 betrachte die Menge
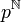 aller Folgen mit Werten aus {1,...,p}. Auf dieser Menge kann man eine Metrik d definieren, indem man d(xk,yk): = p − k setzt, wobei
aller Folgen mit Werten aus {1,...,p}. Auf dieser Menge kann man eine Metrik d definieren, indem man d(xk,yk): = p − k setzt, wobei 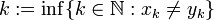 . Ist (xk) = (yk), so sei d(xk,yx): = 0. Aus dem Satz von Tychonoff (siehe unten) folgt, dass der durch diese Metrik induzierte topologische Raum kompakt ist. Diese Konstruktion kann für jede endliche Menge durchgeführt werden, nicht nur für {1,...,p}. Der entstehende metrische Raum ist dabei sogar ultrametrisch. Es gilt folgendes:
. Ist (xk) = (yk), so sei d(xk,yx): = 0. Aus dem Satz von Tychonoff (siehe unten) folgt, dass der durch diese Metrik induzierte topologische Raum kompakt ist. Diese Konstruktion kann für jede endliche Menge durchgeführt werden, nicht nur für {1,...,p}. Der entstehende metrische Raum ist dabei sogar ultrametrisch. Es gilt folgendes:
- Ist p = 2, dann ist die Abbildung
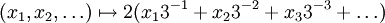 ein Homöomorphismus von
ein Homöomorphismus von 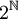 in die Cantor-Menge.
in die Cantor-Menge. - Ist p eine Primzahl, dann ist die Abbildung
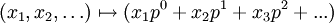 ein Homöomorphismus von
ein Homöomorphismus von 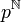 in die p-adischen ganzen Zahlen.
in die p-adischen ganzen Zahlen.
- Ist p = 2, dann ist die Abbildung
- Das Spektrum eines beliebigen stetigen linearen Operators auf einem Hilbertraum ist eine kompakte Teilmenge der Komplexen Zahlen.
- Das Spektrum eines beliebigen kommutativen Ringes oder einer booleschen Algebra ist eine kompakte Teilmenge der Komplexen Zahlen.
Nicht kompakte Räume
- Die reellen Zahlen
 versehen mit der Standardtopologie sind nicht kompakt. Ebenfalls nicht kompakt sind das halboffene Intervall [0,1[, die ganzen Zahlen
versehen mit der Standardtopologie sind nicht kompakt. Ebenfalls nicht kompakt sind das halboffene Intervall [0,1[, die ganzen Zahlen 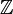 oder die natürlichen Zahlen
oder die natürlichen Zahlen 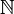 betrachtet als Teilmengen von
betrachtet als Teilmengen von  . Versieht man jedoch beispielsweise
. Versieht man jedoch beispielsweise 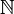 mit der trivialen Topologie
mit der trivialen Topologie 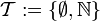 , so ist
, so ist 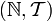 kompakt. Ob eine Menge kompakt ist, hängt daher im Allgemeinen von der gewählten Topologie ab.
kompakt. Ob eine Menge kompakt ist, hängt daher im Allgemeinen von der gewählten Topologie ab. - Die abgeschlossene Einheitskugel des Raumes
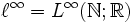 der beschränkten reellen Zahlenfolgen (siehe Lp-Raum), obwohl sie abgeschlossen und beschränkt ist. Es gilt allgemein, dass die Einheitskugel in einem Banachraum genau dann kompakt ist, wenn die Dimension des Raums endlich ist.
der beschränkten reellen Zahlenfolgen (siehe Lp-Raum), obwohl sie abgeschlossen und beschränkt ist. Es gilt allgemein, dass die Einheitskugel in einem Banachraum genau dann kompakt ist, wenn die Dimension des Raums endlich ist.
Eigenschaften
Einige Sätze beziehen sich auf Kompaktheit (siehe Topologie-Glossar für Definitionen):
- Das Bild einer kompakten Menge unter einer stetigen Funktion ist kompakt. Folglich nimmt eine reellwertige stetige Funktion auf einem Kompaktum ein globales Minimum und ein globales Maximum an.
- Eine stetige Funktion auf einem kompakten metrischen Raum ist gleichmäßig stetig. Diese Aussage ist auch als Satz von Heine bekannt.
- Jede unendliche Folge
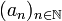 von Elementen einer kompakten Menge
von Elementen einer kompakten Menge 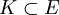 besitzt einen Häufungspunkt. Erfüllt K das erste Abzählbarkeitsaxiom, so existiert sogar eine in K konvergente Teilfolge
besitzt einen Häufungspunkt. Erfüllt K das erste Abzählbarkeitsaxiom, so existiert sogar eine in K konvergente Teilfolge 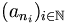 .
.
Die Umkehrung gilt jedoch nicht in jedem topologischen Raum, das heißt eine Teilmenge, in der jede Folge eine (in der Teilmenge) konvergente Teilfolge hat (eine solche Teilmenge heißt folgenkompakt, siehe unten), muss nicht kompakt sein. (Ein Beispiel bildet die Menge der abzählbaren Ordinalzahlen [0,ω1[ mit der Ordnungstopologie.)
- Eine abgeschlossene Teilmenge eines kompakten Raumes ist kompakt.
- Eine kompakte Teilmenge eines Hausdorff-Raumes ist abgeschlossen.
- Eine nicht-leere kompakte Teilmenge der reellen Zahlen hat ein größtes und ein kleinstes Element (siehe auch Supremum, Infimum).
- Für jede Teilmenge M des euklidischen Raumes Rn sind die folgenden drei Aussagen äquivalent (vergleiche Satz von Heine-Borel):
- M ist kompakt, das heißt jede offene Überdeckung von M hat eine endliche Teilüberdeckung.
- Jede Folge in der Menge M hat eine in M konvergente Teilfolge (also mindestens einen Häufungspunkt).
- Die Menge M ist abgeschlossen und beschränkt.
- Ein metrischer Raum ist genau dann kompakt, wenn er vollständig und total beschränkt ist.
- Das Produkt einer beliebigen Klasse von kompakten Räumen ist kompakt in der Produkttopologie. (Satz von Tychonoff -- dies ist äquivalent zum Auswahlaxiom)
- Ein kompakter Hausdorff-Raum ist normal.
- Jede stetige bijektive Abbildung von einem kompakten Raum auf einen Hausdorff-Raum ist ein Homöomorphismus.
- Ein metrischer Raum (oder allgemeiner, ein Raum, der dem ersten Abzählbarkeitsaxiom genügt) ist genau dann kompakt, wenn jede Folge in dem Raum eine konvergente Teilfolge mit ihrem Grenzwert in dem Raum hat.
- Ein topologischer Raum ist kompakt genau dann, wenn jedes Netz auf dem Raum ein Teilnetz hat, das einen Grenzwert in dem Raum hat.
- Ein topologischer Raum ist kompakt genau dann, wenn jeder Filter auf dem Raum eine konvergente Verfeinerung besitzt.
- Ein topologischer Raum ist kompakt genau dann, wenn jeder Ultrafilter auf dem Raum konvergiert.
- Ein topologischer Raum kann in einen kompakten Hausdorff-Raum eingebettet werden genau dann, wenn er ein Tychonoff-Raum ist.
- Jeder topologische Raum X ist ein dichter Unterraum eines kompakten Raumes, der höchstens einen Punkt mehr besitzt als X. (Siehe auch Kompaktifizierung.)
- Ein metrischer Raum X ist kompakt genau dann, wenn jeder zu X homöomorphe metrische Raum vollständig ist.
- Falls der metrische Raum X kompakt ist und eine offene Überdeckung von X gegeben ist, dann existiert eine Zahl δ > 0, so dass jede Teilmenge von X mit Durchmesser < δ in einem Element der Überdeckung enthalten ist. (Zahlen-Lemma von Lebesgue)
- Falls ein topologischer Raum eine Subbasis hat, so dass jede Überdeckung des Raumes durch Elemente der Subbasis eine endliche Teilüberdeckung hat, so ist der Raum kompakt. (Alexanders Subbasis-Satz)
- Zwei kompakte Hausdorff-Räume X1 und X2 sind genau dann homöomorph, wenn ihre Ringe von stetigen reell-wertigen Funktionen C(X1) und C(X2) isomorph sind.
Andere Formen von Kompaktheit
Es gibt einige topologische Eigenschaften, die äquivalent zur Kompaktheit in metrischen Räumen sind, aber nicht äquivalent in allgemeinen topologischen Räumen:
- Folgenkompakt: Jede Folge hat eine konvergente Teilfolge.
- Abzählbar kompakt: Jede abzählbare offene Überdeckung hat eine endliche Teilüberdeckung. (Oder, äquivalent, jede unendliche Teilmenge hat einen ω-Häufungspunkt.)
- Pseudokompakt: Jede reell-wertige stetige Funktion auf dem Raum ist beschränkt.
- Schwach abzählbar kompakt: Jede unendliche Teilmenge hat einen Häufungspunkt.
Während diese Konzepte für metrische Räume äquivalent sind, gibt es im Allgemeinen folgende Beziehungen:
- Kompakte Räume sind abzählbar kompakt.
- Folgenkompakte Räume sind abzählbar kompakt.
- Abzählbar kompakte Räume sind pseudokompakt und schwach abzählbar kompakt.
Siehe auch: Topologie-Glossar, Relativ kompakt
Literatur
- Boto von Querenburg: Mengentheoretische Topologie. 3. Auflage. Springer-Verlag, 2001, ISBN 3-540-09799-6.
Weblinks
- Eine Teilmenge des
Wikimedia Foundation.