- Partielles Wurzelziehen
-
Partielles Radizieren (ugs.: partielles Wurzelziehen oder teilweises Wurzelziehen) bezeichnet eine algebraische Umformung, einen Sonderfall des Radizierens. Der Radikand wird in seine Faktoren zerlegt, so dass durch Anwendung der Wurzelgesetze die Faktoren einzeln betrachtet werden können. Die Wurzel wird dann aus einem oder mehreren Faktoren gezogen.
Beispiel:
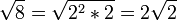
Allgemeine Betrachtung
Wurzeln mit gleichem Wurzelexponenten (n) werden multipliziert, indem man das Produkt der Radikanten (
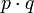 ) mit diesem Exponenten radiziert:
) mit diesem Exponenten radiziert:![\sqrt[n]{p}\cdot\sqrt[n]{q}=\sqrt[n]{p\cdot q}](/pictures/dewiki/51/3676557aa61b807c455d123277091c34.png)
Umgekehrt kann danach die Wurzel aus einem Produkt faktorenweise gezogen werden, man spricht dann von teilweisen oder partiellem Radifizieren:
![\sqrt[p]{p^{n+m}}= \sqrt[n]{p^n}\cdot\sqrt[n]{p^m}=p\cdot\sqrt[n]{p^m}](/pictures/dewiki/49/1bd81a376bb2759c7b1e1970894fc99e.png)
weitere Beispiele
![\sqrt[3]{16a^3b^4}=\sqrt[3]{8}\cdot\sqrt[3]{2}\cdot\sqrt[3]{a^3}\cdot\sqrt[3]{b^3}\cdot\sqrt[3]{b}=2ab\cdot\sqrt[3]{2b}](/pictures/dewiki/53/593b41c7e4aa422508c9adc86b8662d2.png)
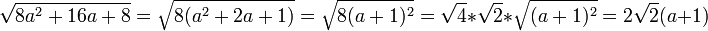
Quellen
- Walter Gellert, Herbert Kästner, Drr Siegfried Neuber (Hrsg.): Fachlexikon ABC MAthematik. VEB, Harri Deutsch, Thun und Frankfurt/Main 1978, ISBN 3871443360, S. 598f..
Wikimedia Foundation.
