Penrose-Muster

Eine Penrose-Parkettierung

Die selbe Parkettierung wie oben mit Hervorhebung kompletter Sterne, zeigt zunehmendes „Chaos“ bei Entfernung von der Mitte

Eine Penrose-Parkettierung ist ein von Roger Penrose und Robert Ammann im Jahr 1973 entdeckte und 1974 publizierte Familie von sogenannten aperiodischen Kachel-Mustern, welche eine Ebene lückenlos parkettieren kann, ohne dass dabei ein Grundschema periodisch wiederholt werden müsste.

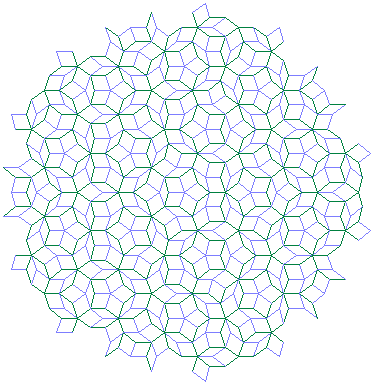
Es gibt mehrere verschiedene Sätze von Penrose-Kacheln; das Bild rechts zeigt ein häufig gewähltes Beispiel. Es besteht aus zwei Rauten, die die gleichen Seitenlängen, aber unterschiedliche Eckwinkel haben:

• die erste Kachel, die dicke Raute, hat Eckwinkel von 72° und 108°,
• die zweite Kachel, die dünne Raute, hat Eckwinkel von 36° und 144°.

Alle Winkel sind also Vielfache von 36°. Beide Kacheln stehen in Verbindung zum goldenen Schnitt, bei der dicken Raute hat die lange Diagonale die Länge 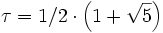$\tau = 1/2 \cdot \left(1 + \sqrt{5} \right)$, die Länge der kurzen Diagonale der dünnen Raute ist 1 / τ. Das Flächenverhältnis der beiden Rauten ist ebenfalls τ, ebenso das Anzahlverhältnis der bei der Parkettierung insgesamt verwendeten Kacheln.

In beiden Kacheln taucht das Verhältnis τ des goldenen Schnitts auf.

Beim Zusammenfügen der Kacheln muss beachtet werden, dass diese nicht beliebig aneinandergefügt werden dürfen. Das Anbringen von Ausbuchtungen und Einkerbungen an den Kacheln (wie bei Puzzleteilen) kann das ausschließlich korrekte Zusammenfügen sicherstellen, alternativ auch Farbmuster, die nur passend zusammengefügt werden dürfen. Aus ästhetischen Gründen wird die Parkettierung meist mit geraden Kanten dargestellt. Die oft fälschlich genannte Parallelogrammregel, die verbietet, dass zwei Kacheln so zusammengesetzt werden, dass sie gemeinsam ein Parallelogramm bilden, ist jedenfalls nicht ausreichend, um eine periodische Parkettierung zu verhindern.

Kacheln mit Ausbuchtungen/Einkerbungen sowie Farbmustern. Jede dieser zwei Methoden verhindert, dass (auch) periodische Parkettierungen möglich sind.

Eine Parkettierung, die die Parallelogrammregel verletzt.

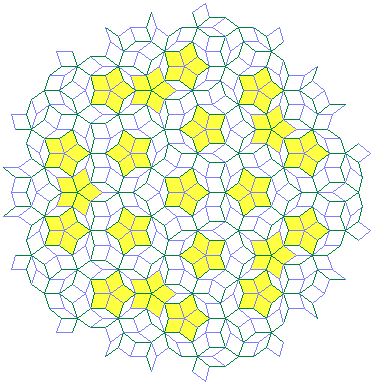
Beachtet man diese Regel, so erhält man viele (sogar unendlich viele) verschiedene Parkettierungen der Ebene, d. h. Überdeckungen „ohne Löcher“, die sich unendlich fortsetzen lassen. Die Bilder zeigen zwei Beispiele, die darüber hinaus eine fünffache Rotationssymmetrie und fünf Spiegelsymmetrien aufweisen. Es gibt in diesen Mustern aber keine Translationssymmetrie, d. h. die Muster sind aperiodisch. Jedoch kann man zeigen, dass jeder endliche Ausschnitt eines solchen Musters sich unendlich oft wiederfindet (und zwar sogar auch in jeder anderen aus den gleichen Kacheln bestehenden Penrose-Parkettierung).

Die Tatsache, dass es möglich ist, die Ebene mit einer aperiodischen Parkettierung zu überdecken, wurde zuerst 1966 (o. 1964) von Robert Berger bewiesen, der kurz darauf ein konkretes Beispiel mit 20426 verschiedenen Kacheln angeben konnte. In der Folge wurden immer kleinere Sätze von Kacheln für eine solche aperiodische Parkettierung angegeben, bis Penrose schließlich die Zahl der Kacheln auf zwei reduzieren konnte. Neben den erwähnten rhombischen Kacheln gibt es noch ein weiteres Paar von Kacheln, die eine aperiodische Parkettierung liefern, genannt „Drachen“ und „Pfeil“. Ob eine einzelne Kachelform existiert, mit der sich nur aperiodische Parkettierungen realisieren lassen, ist unbekannt.

Alternative Kacheln: Drachen und Pfeil.

Aperiodische Parkettierungen wurden zuerst nur als interessante mathematische Struktur betrachtet, aber inzwischen wurden Materialien gefunden, in denen die Atome wie in Penrose-Kacheln angeordnet sind. Diese Materialien können keine periodischen Kristalle bilden, aber Quasikristalle, da sich die Muster „fast“ wiederholen.

Islamische Vorläufer

Bei einer Reise durch Usbekistan 2007 fielen Peter Lu von der Harvard-Universität, der auf dem Gebiet der Quasikristalle arbeitet, an einem Gebäude Kachelornamente auf, die ihn an Penrose-Parkettierungen erinnerten. Bei der Sichtung vieler Fotografien stieß er auf Arbeiten im Darb-i-Imam-Schrein in Isfahan, Iran, aus dem 15. Jahrhundert, welche die Ergebnisse von Penrose vorwegzunehmen scheinen.

Diese Kachelornamentik hat klar ersichtlich ihre Anfänge im Sinne von sich nicht wiederholbaren unendlichen Parkettierungen bereits ab dem 12. Jahrhundert (wie Markovicky am Gonbad-e-Kabud in Maragha 1992 zeigte), wobei ein Satz mit fünf einfach zu konstruierenden Grundformen, die sogenannten Girih-Kacheln, zum Einsatz kamen. Anders als z.B. für keltische Knoten, bei denen die Konstruktion der Muster nachvollziehbar^[1] ist, liegen für die Methoden zur konstruktiven Mustererzeugung in diesem Fall aber noch keine Anhaltspunkte vor. Ab dem 15. Jahrhundert wurde die Ausführungen weiterhin um die Eigenschaft der Selbstähnlichkeit, wie man sie unter anderem bei Fraktalen kennt, ergänzt.

Derzeit sind noch keinerlei Funde von Schablonen bekannt, welche die angesprochenen Grundformen repräsentieren. Einerseits hätte man sie in früheren Jahren der archäologischen Forschung wohl nur schwer als solche erkennen können, andererseits besteht auch die Möglichkeit, dass diese nicht dauerhaft genug waren oder eventuell sogar nach den Arbeiten zerstört wurden. Der Einsatz eines solchen Systems belegt zumindest, dass die Anwendung desselben verstanden und beherrscht wurde und für die Ornamentik-Arbeiten gezielt benutzt wurde. Inwieweit dies ein Hinweis auf ein tiefer gehendes, mathematisches Verständnis der Beteiligten im Bereich der Strukturen und Muster ist, ist derzeit offen.

Literatur

• Computerdenken – Des Kaisers neue Kleider oder Die Debatte um Künstliche Intelligenz, Bewußtsein und die Gesetze der Natur. Mit einem Vorwort von Martin Gardner und einem Vorwort zur deutschen Ausgabe von Dieter Wandschneider. Heidelberg 1991. ISBN 3-8274-1332-X
• The Emperor’s New Mind. Penguin Books, New York 1991. ISBN 0-14-014534-6 (Englische Originalausgabe)
• Roger Penrose: Set of tiles for covering a surface. Patent vom 9. Januar 1979. Patent US 4133152
• Martin Gardner: Penrose Tiles. Kapitel 7, in: The Colossal Book of Mathematics. Norton, New York NY 2001. ISBN 0-393-02023-1
• Peter Lu und Paul Steinhardt: Decagonal and Quasi-crystalline Tilings in Medieval Islamic Architecture. In: Science. Band 315, Washington 2007, S. 1106–1110. ISSN 0036-8075
• Emil Markovicky: 800-Year-Old Pentagonal Tiling From Maragha, Iran, and the New Varieties of Aperiodic Tiling it Inspired. In: István Hargittai (Hrsg.): Fivefold Symmetry. World Scientific, Singapore/River Edge NJ 1992, S. 67–86. ISBN 981-02-0600-3
• Roger Penrose: Pentaplexity - A Class of Non-Periodic Tilings of the Plane. In: The Mathematical Intelligencer. Band 2, Nr. 1, Springer, New York 1979, S.32–37 (Nachdruck aus Eureka No. 39). ISSN 0343-6993
• Roger Penrose: The role of aesthetics in pure and applied mathematical research. In: Bulletin of the Institute of Mathematics and Its Applications (Bull. Inst. Math. Appl.). Southend-on-Sea Band 10, 1974, S. 266-271. ISSN 0146-3942
• Christoph Pöppe: Quasikristalle in neuem Licht. In: Spektrum der Wissenschaft. Heidelberg 7/1999, S. 14–17. ISSN 0170-2971
• P. Stephens, A. Goldman: Die Struktur der Quasikristalle. In: Spektrum der Wissenschaft. Heidelberg 6/1991, S. 48–56. ISSN 0170-2971
• Martin Gardner: Mathematische Spielereien. In: Spektrum der Wissenschaft. Heidelberg 11/1979, S. 22–33. ISSN 0170-2971

Weblinks

• Ein kostenloses Windows-Programm zur Erzeugung von Penrose-Parkettierungen. Das Programm wurde von Stephen Collins (JKS Software) in Zusammenarbeit mit den Universitäten von York (Großbritannien) and Tsuka (Japan) entwickelt.
• Zwei Theorien über die Bildung von Quasicrystals mit Ähnlichkeiten zu Penrose-Parkettierungen
• NUMERATOR Moschee-Baumeister waren westlichen Mathematikern 500 Jahre voraus

Einzelnachweise

1. ↑ Keltischer Knoten