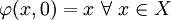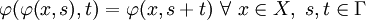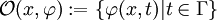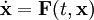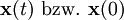Phasenfluss

Das Konzept eines (Phasen-)Flusses in der Mathematik ermöglicht die Beschreibung zeitabhängiger (System-)Zustände. Es ist deshalb vor allem für die Analyse gewöhnlicher Differentialgleichungen von Bedeutung und findet damit Anwendung in vielen Bereichen der Mathematik und Physik. Formal ist der Fluss eine Gruppenoperation einer Parametergruppe (Γ, + ) auf einer Menge X.

Definition

Sei X eine Menge, Γ eine Parametermenge. Eine Abbildung

$\varphi:X\times\Gamma\to X$

heißt Fluss, wenn die folgenden Bedingungen erfüllt sind:

$\varphi(x,0)=x\ \forall\ x\in X$

und

$\varphi(\varphi(x,s),t)=\varphi(x,s+t)\ \forall\ x\in X,\ s,t\in\Gamma$

Wir haben also eine Halbgruppenwirkung.

Die Menge

$\mathcal{O}(x,\varphi):=\left\{\varphi(x,t)|t\in\Gamma\right\}$

heißt Orbit von x.

Falls die Abbildung 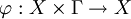$\varphi: X\times\Gamma\to X$ differenzierbar ist, spricht man auch von einem differenzierbaren Fluss.

Diskussion

Im Hinblick auf die Analyse dynamischer Systeme beschreibt der Fluss die Bewegung im Phasenraum im Laufe der Zeit. Hierbei spricht man in Abhängigkeit von der Parametermenge Γ von einem kontinuierlichen dynamischen System (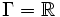$\Gamma=\mathbb{R}$) oder einem diskreten dynamischen System ($\Gamma=\mathbb{N}$).

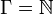Betrachten wir ein System gewöhnlicher Differentialgleichungen

$\dot{\mathbf{x}}=\mathbf{F}(t,\mathbf{x})$

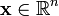mit $\mathbf{x}\in\mathbb{R}^n$ oder einer offenen Teilmenge davon, so werden durch den Phasenfluss die Lösungen dieses Systems in Abhängigkeit vom Anfangszustand angegeben. Man wählt dann oft auch eine implizite Form der Flussangabe und schreibt

$\mathbf{x}(t)\text{ bzw. }\mathbf{x}(0)$

Literatur

• Manfred Denker: Einführung in die Analysis dynamischer Systeme. Springer Verlag, Berlin, Heidelberg, New York 2005, ISBN 3-540-20713-9
• Werner Krabs: Dynamische Systeme: Steuerbarkeit und chaotisches Verhalten. B.G.Teubner, Leipzig 1998, ISBN 3-519-02638-4.