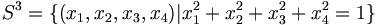Poincare-Vermutung

Die Poincaré-Vermutung galt lange als das bedeutendste ungelöste Problem in der Topologie, einem Teilgebiet der Mathematik. Sie ist benannt nach Henri Poincaré und wurde von diesem 1904 aufgestellt. Im Jahr 2000 zählte das Clay Mathematics Institute die Poincaré-Vermutung unter die sieben bedeutendsten ungelösten mathematischen Probleme und lobte für die Lösung einen Preis von einer Million US-Dollar aus. Nach allgemeiner Expertenansicht ist die Vermutung inzwischen durch Grigori Perelman bewiesen.

Wortlaut und Beschreibung

Jede einfach zusammenhängende kompakte unberandete 3-dimensionale Mannigfaltigkeit ist homöomorph zur 3-Sphäre.

Eine fachsprachlich genauere Formulierung ist:

Eine kompakte unberandete 3-dimensionale Mannigfaltigkeit hat genau dann eine triviale Fundamentalgruppe, wenn sie homöomorph zur 3-Sphäre ist.

Darüber hinaus gibt es noch eine Verallgemeinerung der Vermutung auf n-dimensionale Mannigfaltigkeiten in der folgenden Form:

Jede geschlossene n-Mannigfaltigkeit mit dem Homotopietyp einer n-Sphäre ist zur n-Sphäre homöomorph.

Für den Fall n = 3 stimmt diese verallgemeinerte Vermutung mit der ursprünglichen Poincaré-Vermutung überein.

Vereinfacht kann man die Poincaré-Vermutung so beschreiben: Die Oberfläche einer Kugel ist 2-dimensional, beschränkt, randlos und jede geschlossene Kurve lässt sich auf einen Punkt zusammenziehen, welcher auch auf der Kugel liegt. Sie ist (topologisch gesehen) auch das einzige 2-dimensionale Gebilde mit diesen Eigenschaften. Bei der Poincaré-Vermutung geht es um das 3-dimensionale Analogon: Hier geht es um eine 3-dimensionale „Oberfläche“ eines 4-dimensionalen Körpers.

Erläuterungen

Mannigfaltigkeit

Eine 3-dimensionale Mannigfaltigkeit ist etwas, das in einer Umgebung jedes Punktes auf der Mannigfaltigkeit wie ein 3-dimensionaler euklidischer Raum aussieht.

Geschlossen

Geschlossen bedeutet in diesem Zusammenhang, dass die Mannigfaltigkeit beschränkt ist (also sich nicht ins Unendliche ausdehnt), und dass sie keinen Rand hat. Eine dreidimensionale Kugel ist etwa eine 3-Mannigfaltigkeit, aber sie hat einen Rand (die Oberfläche), daher ist sie nicht geschlossen. Ihre Oberfläche ist dagegen eine geschlossene 2-dimensionale Mannigfaltigkeit. Die Poincaré-Vermutung stellt nur eine Behauptung für geschlossene Mannigfaltigkeiten auf.

Einfach zusammenhängend

Einfach zusammenhängend bedeutet, dass man jede geschlossene Kurve auf einen Punkt zusammenziehen kann. Ein Gummiband auf einer Kugeloberfläche lässt sich immer so auf der Oberfläche verschieben, dass es zu einem Punkt wird. Auf einem Torus (etwa einem Fahrradschlauch) beispielsweise funktioniert das Zusammenziehen nicht immer: Wenn das Gummiband rund um die dünnere Seite des Fahrradschlauches läuft, kann man es nie zu einem Punkt zusammenziehen (man müsste den Schlauch zerschneiden, was in der Topologie nicht erlaubt ist). Daher ist ein Torus nicht einfach zusammenhängend.

3-Sphäre

Allgemein ist eine n-Sphäre (Bezeichnung: Sⁿ) der Rand einer (n+1)-dimensionalen Kugel. Eine 1-Sphäre ist der Rand eines Kreises. Eine 2-Sphäre ist die Oberfläche einer 3-dimensionalen Kugel. Eine 3-Sphäre ist die Oberfläche einer 4-dimensionalen Kugel. Dieses Objekt kann man sich natürlich nicht mehr einfach vorstellen, weil es eigentlich in einem 4-dimensionalen Raum „lebt“. Mathematisch kann man die 3-Sphäre leicht durch eine Formel beschreiben, nämlich als die Menge aller Punkte im 4-dimensionalen Raum, die den Abstand 1 vom Nullpunkt haben:

$S^3 = \{(x_1,x_2,x_3,x_4)| x_1^2 + x_2^2 + x_3^2 + x_4^2 =1 \}$

Eine 2-Sphäre besteht aus zwei (hohlen) Halbkugeln, die an den Rändern zusammengefügt sind. Topologisch sind diese hohlen Halbkugeln eigentlich Kreisflächen (wenn man sie von oben plattdrückt, entstehen zwei Scheiben). Damit kann man eine 2-Sphäre erhalten, indem man zwei Kreisflächen an den Rändern zusammenklebt. Genauso kann man ein relativ anschauliches Bild einer 3-Sphäre konstruieren. Man nimmt zwei Kugeln (entspricht den Kreisflächen im 2-Dimensionalen) und „klebt“ sie an den entsprechenden Punkten der Oberfläche zusammen. Ein Weg auf der 3-Sphäre beginnt damit in einer der beiden Kugeln. Wenn man zum Rand kommt, dann springt man auf den entsprechenden Punkt der zweiten Kugel und umgekehrt. Auf diese Weise kann man Wege auf der 3-Sphäre im 3-dimensionalen Raum beschreiben. Man sieht auf diese Weise auch, dass es nirgendwo einen Rand gibt. Damit ist die 3-Sphäre geschlossen.

Die Vermutung in höheren Dimensionen

Für n größer als 3 benötigt man den technischen Begriff der Homotopie. Zwei Mannigfaltigkeiten haben den gleichen Homotopietyp, wenn ihre Homotopiegruppen übereinstimmen. Für den Fall n=3 gilt wegen des Satzes von Hurewicz und der Poincaré-Dualität die Aussage, dass eine einfach zusammenhängende Mannigfaltigkeit den gleichen Homotopietyp wie die 3-Sphäre hat. Damit ist die n-dimensionale Formulierung zur normalen Poincaré-Vermutung äquivalent.

Geschichte

Ursprünglich hatte Poincaré eine etwas andere Vermutung aufgestellt: Er glaubte, dass jede geschlossene Mannigfaltigkeit, die die gleiche Homologie (nicht Homotopie!) wie eine Sphäre besitzt, schon topologisch eine Sphäre sein muss. Dabei bedeutet „die Homotopie einer Sphäre zu haben“, dass jede topologisch in die Mannigfaltigkeit immersierte (n − 1)-Sphäre der Rand einer immersierten n-dimensionalen Kugel in der Mannigfaltigkeit ist. Die entsprechende Homologie zu haben bedeutet jedoch nur, dass jede immersierte (n − 1)-Sphäre der Rand eines beliebigen n-dimensionalen simplizialen Komplexes ist. Poincaré glaubte ursprünglich, einen Beweis zu haben, der mit dieser schwächeren Voraussetzung auskommt. Bald darauf entdeckte er jedoch selbst einen Fehler und fand mit der Poincaré-Homologiesphäre ein Gegenbeispiel zur ursprünglichen Vermutung in Dimension drei: Sie hat triviale Homologie, aber nicht-triviale Homotopie, da sie nicht einfach zusammenhängend ist. Daher änderte er seine Vermutung auf die heute bekannte Aussage.

Für n = 2 ist die Aussage bewiesen; in diesem Fall sind sogar alle (geschlossenen) 2-dimensionalen Mannigfaltigkeiten bekannt und klassifiziert.

Im Fall n > 4 ist die Vermutung ebenso bewiesen. Stephen Smale hat diesen Beweis 1960 präsentiert und erhielt unter anderem dafür die Fields-Medaille. Michael Freedman löste den Fall n = 4 im Jahre 1982. Auch er erhielt dafür 1986 die Fields-Medaille.

Der Fall n = 3 hat sich (nicht überraschend) als der schwierigste erwiesen. Viele Mathematiker haben Beweise vorgelegt, die sich dann aber als falsch erwiesen. Dennoch haben einige dieser fehlerhaften Beweise das Verständnis der niedrig-dimensionalen Topologie erweitert.

Gegenwärtiger Beweis

Ende des Jahres 2002 tauchten Meldungen auf, Grigori Perelman vom Steklow-Institut in Sankt Petersburg habe die Vermutung bewiesen. Er verwendet die von Richard Hamilton entwickelte analytische Methode des Ricci-Flusses, um die allgemeinere Vermutung der Geometrisierung von 3-Mannigfaltigkeiten zu beweisen, aus der die Poincaré-Vermutung als Spezialfall folgt. Dabei veröffentlichte Perelman seine Arbeiten nicht, wie vom Clay Mathematics Institute gefordert, in einer begutachteten Zeitschrift, sondern im Online-Archiv arXiv und erklärte zugleich, er sei nicht materialistisch. Die sich über mehrere Publikationen erstreckende und insgesamt etwa 70 Seiten umfassende Beweiskette wurde seitdem von Mathematikern weltweit überprüft. In Anerkennung der Richtigkeit seines Beweises wurde Grigori Perelman 2006 beim Internationalen Mathematikerkongress in Madrid die Fields-Medaille verliehen, die er aber, wie angekündigt, nicht angenommen hat.

Da Perelman selbst kein Interesse an einer detaillierteren Darstellung seines Beweises zeigt, haben verschiedene Gruppen von Mathematikern dies übernommen: So haben Bruce Kleiner und John Lott bereits bald nach Bekanntwerden von Perelmans Arbeiten ihre Ausarbeitung vieler Details veröffentlicht und immer wieder zu inzwischen 192 Seiten ergänzt. John Morgan und Gang Tian haben eine vollständige Ausarbeitung von 474 Seiten im Juli 2006 auf dem arXiv veröffentlicht. Auch Huai-Dong Cao und Xi-Ping Zhu veröffentlichen 2006 einen Beweis der Poincaré-Vermutung und der Geometrisierung, indem sie den Beweis von Perelman auf 300 Seiten genau ausgearbeitet darlegten.

Damit wurde die Poincaré-Vermutung allen bisherigen Einschätzungen zufolge bewiesen.

Bedeutung der Vermutung

Der Beweis der Poincaré-Vermutung ist ein wichtiger Beitrag zur Klassifizierung aller 3-Mannigfaltigkeiten. Dies liegt daran, dass Perelman eigentlich die allgemeinere Geometrisierungsvermutung geschlossener 3-Mannigfaltigkeiten beweist, die die Poincaré-Vermutung als einen Spezialfall enthält.

Literatur

• Grisha Perelman: The entropy formula for the Ricci flow and its geometric applications. Preprint 2002. (Englisch)
• Grisha Perelman: Ricci flow with surgery on three-manifolds. Preprint 2003. (Englisch)

• Bruce Kleiner, John Lott: Notes on Perelman's papers. (Detaillierte Ausarbeitung einzelner Argumente und Beweise von Perelman)

• John Morgan, Gang Tian: Ricci Flow and the Poincaré Conjecture. (Detaillierter Beweis der Poincaré-Vermutung, englisch).

• Huai-Dong Cao, Xi-Ping Zhu: A Complete Proof of the Poincaré and Geometrization Conjectures - Application of the Hamilton-Perelman theory of the Ricci flow. in: Asian Journal of Mathematics. International Press, Boston Mass 10.2006, 2 (June), 165-492. ISSN 1093-6106 (Abstract)

• John Milnor: The Poincaré Conjecture 99 Years Later. A Progress Report. (Englisch)

• John Milnor: Towards the Poincaré conjecture and the classification of 3-manifolds. (Englisch)

• Bernhard Leeb: Übersichtsartikel für die DMV-Mitteilungen (PDF)

populärwissenschaftlich

• Donal O'Shea: Poincarés Vermutung. Die Geschichte eines mathematischen Abenteuers. S. Fischer, Frankfurt am Main 2007. ISBN 3-10-054020-4

• George G. Szpiro: Das Poincaré-Abenteuer. Ein mathematisches Welträtsel wird gelöst. Piper, München 2008. ISBN 3-492-05130-8

Weblinks

• Beschreibung der Poincaré-Vermutung am Clay Mathematics Institute (Englisch)
• Notes and commentary on Perelman's Ricci flow papers Übersicht über verschiedene Quellen zum Ricci-Fluss (Englisch)
• Bericht in „The New Yorker“ zur Geschichte des Beweises und mit Hintergründen zu den Beteiligten (Englisch)
• Artikel aus dem „Boston Globe“ (Englisch)
• Bericht in „Die Zeit“ von 2003