Poincarégruppe

Die Poincaré-Gruppe (benannt nach dem französischen Mathematiker und Physiker Henri Poincaré) ist eine spezielle Gruppe in der Mathematik, die Anwendungen in der Physik gefunden hat.

Historisches

Die Gruppe taucht historisch zum ersten Mal bei der Untersuchung der Invarianzen der Elektrodynamik durch Poincaré, Lorentz und andere auf und spielte eine entscheidende Rolle bei der Formulierung der speziellen Relativitätstheorie. Insbesondere wurde die Poincaré-Gruppe nach der Formalisierung der Relativitätstheorie durch Hermann Minkowski zu einer wichtigen mathematischen Struktur in allen relativistischen Theorien, darunter in der Quantenelektrodynamik.

Geometrische Definition

Die Poincaré-Gruppe ist die affine Invarianzgruppe des pseudo-euklidischen Minkowskiraumes 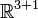$\mathbb{R}^{3+1}$, insbesondere ist der Minkowskiraum bezüglich der Poincaré-Gruppe ein homogener Raum, dessen Geometrie sie im Sinne des Erlanger Programms definiert. Sie unterscheidet sich von der Lorentz-Gruppe, die die lineare Invarianzgruppe des Minkowskiraums ist, durch die Hinzunahme von Translationen. Sie ähnelt daher in ihrer Struktur der euklidischen Gruppe im dreidimensionalen Raum, die alle geometrischen Kongruenzabbildungen enthält. Tatsächlich ist die Euklidische Gruppe als Untergruppe in der Poincaré-Gruppe enthalten. Der wesentliche Unterschied besteht jedoch darin, dass die Poincaré-Gruppe nicht die Längen und Winkel im dreidimensionalen Raum erhält, sondern die bezüglich des indefiniten Pseudo-Skalarprodukts im Minkowskiraum definierten Längen und Winkel. Insbesondere erhält sie so genannte Eigenzeitabstände in der speziellen Relativitätstheorie.

Algebraische Definition

Die Poincaré-Gruppe ist das semidirekte Produkt der Lorentzgruppe O(3,1) und der Gruppe der Translationen im 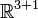$\mathbb{R}^{3+1}$. Jedes Element der Poincaré-Gruppe ist also als Paar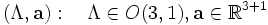

$(\Lambda, \mathbf{a}):\quad \Lambda \in O(3,1), \mathbf{a}\in \mathbb{R}^{3+1}$

darstellbar, und die Gruppenmultiplikation ist durch

$(\Lambda, \mathbf{a})\cdot (\Lambda', \mathbf{a}')=(\Lambda\cdot \Lambda',\mathbf{a}+\Lambda(\mathbf{a}'))$

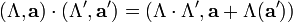
gegeben, wobei die Lorentztransformation Λ in ihrer natürlichen Wirkung als Automorphismus auf 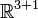$\mathbb{R}^{3+1}$ wirkt.

Weitere Eigenschaften

Die Poincaré-Gruppe ist eine 10-dimensionale nicht-kompakte Liegruppe. Sie ist ein Beispiel einer nicht halbeinfachen Gruppe.

Die Lie-Algebra der Poincaré-Gruppe wird durch die folgenden Relationen definiert:

$\begin{align} {}[P_\mu, P_\nu] &= 0 \\ {}[M_{\mu\nu}, P_\kappa] &= \eta_{\mu\kappa} P_\nu-\eta_{\nu\kappa} P_\mu \\ {}[M_{\mu\nu}, M_{\kappa\lambda}] &= \eta_{\mu\kappa} M_{\nu\lambda}- \eta_{\mu\lambda} M_{\nu\kappa}- \eta_{\nu\kappa} M_{\mu\lambda} + \eta_{\nu\lambda} M_{\mu\kappa} \end{align}$

wobei P_μ die vier infinitesimalen Erzeuger der Translationen und M_μν die sechs infinitesimalen Erzeuger der Lorentz-Tansformationen sind.