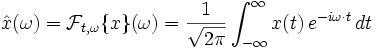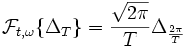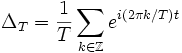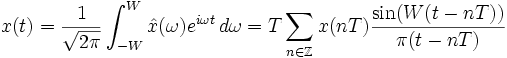Poissonsche Summationsformel

Die Poissonsche Summenformel ist ein wichtiges Hilfsmittel der Fourier-Analysis und Signalverarbeitung. Sie dient u. a. zur Analyse der Eigenschaften von Abtastmethoden.

Formulierung der Aussage

Sei 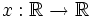$x:\R\to\R$ eine stetige, im Unendlichen schnell fallende Funktion. Es seien die Fourier-Transformierten in den zwei wichtigsten Varianten gleichzeitig betrachtet,

$\hat x(\omega)=\mathcal{F}_{t,\omega}\{x\}(\omega) =\frac1{\sqrt{2\pi}}\int_{-\infty}^\infty x(t)\,e^{-i\omega\cdot t}\,dt$

bzw.

$X(\nu)=\mathcal{F}_{t,\nu}\{x\}(\nu) =\int_{-\infty}^\infty x(t)\,e^{-i(2\pi\nu)t}\,dt$.

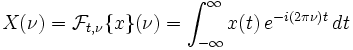Dann gilt, unter geeigneten weiteren Einschränkungen, für jede Intervalllänge T > 0

$T\sum_{n\in\Z}x(nT) =\sqrt{2\pi}\sum_{k\in\Z}\hat x\left(\frac{2\pi k}{T}\right) =\sum_{k\in\Z}X\left(\frac kT\right)$.

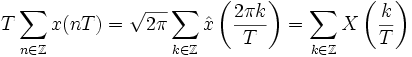Unter Ausnutzung der elementaren Eigenschaften der Fourier-Transformation ergibt sich daraus die allgemeinere Formel mit zusätzlichen Parametern $t,\nu\in\R$:

$T\sum_{n\in\Z}x(t+nT)e^{-i(2\pi\nu)nT} =\sqrt{2\pi}\sum_{k\in\Z}\hat x\left(2\pi\nu+\frac{2\pi k}{T}\right)e^{i\,2\pi(\nu+k/T)t} =\sum_{k\in\Z}X\left(\nu+\frac kT\right)e^{i\,2\pi(\nu+k/T)t}$.

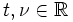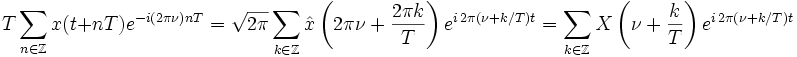Geeignete Voraussetzungen sind z. B. dass die Funktion x zweifach stetig differenzierbar ist und der Ausdruck $(1+t^2)\,(|x(t)+|x''(t)|)$ beschränkt ist. Setzt man in der allgemeineren Form t = 0,

$T\sum_{n\in\Z}x(nT)e^{-i(2\pi\nu)nT} =\sqrt{2\pi}\sum_{k\in\Z}\hat x\left(2\pi\nu+\frac{2\pi k}{T}\right) =\sum_{k\in\Z}X\left(\nu+\frac kT\right)$,

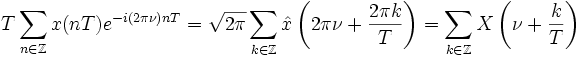so kann die Poissonsche Summenformel auch als Identität einer Fourier-Reihe mit Funktionswerten von x als Koeffizienten auf der linken Seite und einer Periodisierung der Fourier-Transformierten von x auf der rechten Seite gelesen werden. Diese Identität gilt mit Ausnahme einer Menge vom Maß Null, wenn x eine bandbeschränkte Funktion ist, d. h. die Fourier-Transformierte eine messbare Funktion in 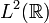$L^2(\R)$ mit kompaktem Träger ist.

Formulierung mittels Dirac-Kamm

Ist x sogar eine temperierte Funktion, d. h. gehört dem Schwartz-Raum 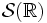$\mathcal S(\mathbb R)$ an, so kann die Poissonsche Summenformel mittels zweier Dirac-Kämme geschrieben werden. Der Dirac-Kamm zur Intervalllänge T ist definiert als

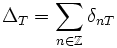$\Delta_T=\sum_{n\in\mathbb Z}\delta_{nT}$, d. h. $\langle \Delta_T,\,x\rangle=\sum_{n\in\mathbb Z}x(nT)$.

Die Summenformel nimmt daher die Gestalt

$T\langle \Delta_T,\,x\rangle =\sqrt{2\pi}\langle \Delta_{2\pi/T},\,\hat x\rangle =\langle \Delta_{1/T},\,X\rangle$

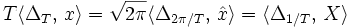
an.

In der Sprache der temperierten Distributionen ist die Fourier-Transformierte einer Distribution 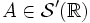$A\in\mathcal S'(\mathbb R)$ diejenige temperierte Distribution 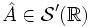$\hat A \in\mathcal S'(\mathbb R)$, für welche in Analogie zur Plancherel-Identität die Identität

$\langle \hat A,\,\hat \phi\rangle=\langle A,\,\phi\rangle$

für jede Testfunktion 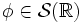$\phi\in\mathcal S(\mathbb R)$ aus dem Schwartz-Raum gilt. In diesem Sinne kann die Poissonsche Summenformel auch als Aussage über die Fourier-Transformierte des Dirac-Kamms gelesen werden:

$\mathcal F_{t,\omega}\{\Delta_T\}=\frac{\sqrt{2\pi}}{T}\Delta_{\frac{2\pi}T}$

bzw.

$\mathcal F_{t,\nu}\{\Delta_T\}=\frac{1}{T}\Delta_{\frac1T}$.

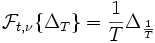Eine gängige Fehldarstellung

Oft, mitunter auch in Lehrbüchern, befindet sich die Behauptung, dass der Dirac-Kamm als periodische Distribution in eine Fourier-Reihe entwickelbar wäre und dass deshalb

$\Delta_T=\frac1T\sum_{k\in\Z}e^{i(2\pi k/T)t}$

eine Kurzdarstellung der Poissonschen Summenformel wäre. Diese Darstellung ist zu vermeiden, denn

• es wird fälschlich suggeriert, dass eine echte Distribution, die keine reguläre Distribution ist, zu einer „normalen“ Funktion identisch wäre und
• die auf der rechten Seite stehende Funktionenreihe konvergiert fast nirgendwo, d. h. die Funktion auf der rechten Seite gibt es gar nicht.

Um den zweiten Grund einzusehen, muss man sich nur die Partialsummen der Funktionenreihe ansehen. Nach der Formel für die geometrische Summe gilt

$\sum_{k=-M}^Ne^{i(2\pi k/T)t} =\frac{e^{i\,2\pi(N+1)\,t/T}-e^{-i\,2\pi M\,t/T}}{e^{i\,2\pi t/T}-1} =e^{i\,\pi(N-M)\,t/T}\cdot\frac{\sin(\pi(N+M+1)\,t/T)}{\sin(\pi\,t/T)}$.

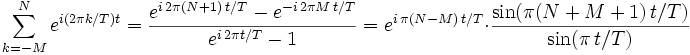Abgesehen von den Vielfachen von T, für welche die Reihe divergiert, oszilliert die Folge der Partialsummen für jedes t bei $M,N\to\infty$. Es ist sinnlos, die Gleichheit zu einem Gebilde, welches gar nicht existiert, zu behaupten.

Zum Beweis

Mit der Eigenschaft des schnellen Fallens im Unendlichen sei vorausgesetzt, dass die Periodisierung

$g(t):=T\sum_{n\in\mathbb Z}x(t+nT)$

stetig, beschränkt und stückweise differenzierbar ist. g ist periodisch mit Periode T, kann also in eine punktweise konvergente Fourier-Reihe entwickelt werden,

$g(t)=\sum_{k\in\mathbb Z} c_k\cdot e^{i2\pi\cdot kt/T}$.

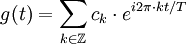Deren Fourier-Koeffizienten bestimmen sich nach der Formel

$c_k=\frac1T\int_{0}^{T} g(t)\cdot e^{-i2\pi\cdot kt/T}\,dt =\int_{0}^{T} \sum_{n\in\mathbb Z}x(t+nT)\cdot e^{-i2\pi\cdot k(t/T+n)}\,dt$.

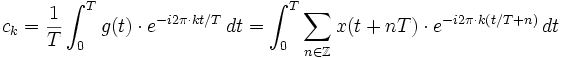Ebenfalls aus dem schnellen Abfall im Unendlichen folgt, dass die Reihe mit der Integration vertauscht werden kann. Daher gilt mit s=t+nT weiter

$c_k=\sum_{n\in\mathbb Z}\int_{nT}^{nT+T}x(s)\cdot e^{-i2\pi\cdot ks/T}\,ds =\int_{-\infty}^\infty x(s)\cdot e^{-i(2\pi k/T)s}\,ds=\sqrt{2\pi}\hat x(2\pi k/T)=X(k/T)$.

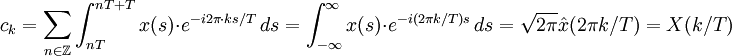Wir können also zusammenfassen zu

$T\sum_{n\in\mathbb Z}x(t+nT) =\sqrt{2\pi}\sum_{k\in\mathbb Z}\hat x(2\pi k/T)\cdot e^{i(2\pi\cdot k/T)t} =\sum_{k\in\mathbb Z}X(k/T)\cdot e^{i(2\pi\cdot k/T)t}$,

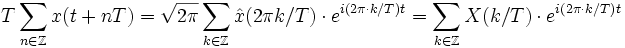woraus sich bei t=0 die Behauptung ergibt.

Anwendung auf bandbeschränkte Funktionen

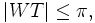Sei x bandbeschränkt mit höchster Frequenz W, d. h. $supp \hat x\subset [-W,W]$. Ist dann $|WT|\le \pi,$ so tritt in der rechten Seite der Summenformel nur ein Summand auf, mit den Ersetzungen $\omega:=-2\pi\nu\in[-W,W]$, t=0 und Multiplikation eines Faktors erhält man

$\sqrt{2\pi}\hat x(\omega)e^{i\omega t}=T\sum_{n\in\mathbb Z} x(nT)e^{i\omega(t-nT)}$.

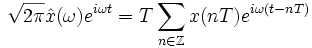Nach Multiplikation mit der Indikatorfunktion des Intervalls [-W,W] und nachfolgend der inversen Fourier-Transformation ergibt sich

$x(t)=\frac1{\sqrt{2\pi}}\int_{-W}^W\hat x(\omega)e^{i\omega t}\,d\omega =T\sum_{n\in\mathbb Z}x(nT)\frac{\sin(W(t-nT))}{\pi(t-nT)}$

Im Grenzfall WT = π ist dies die Rekonstruktionsformel des Nyquist-Shannon-Abtasttheorems

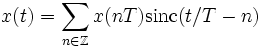$x(t)=\sum_{n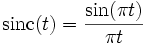\in\mathbb Z}x(nT)\operatorname{sinc}(t/T-n)$ mit $\operatorname{sinc}(t)=\frac{\sin(\pi t)}{\pi t}$.

siehe auch

Literatur:

• J.R. Higgins: Five short stories about the cardinal series. Bull. AMS 12(1985)1
• J.J. Benedetto; G. Zimmermann: Sampling multipliers and the Poisson summation formula. Preprint im [Netz], J. Fourier Ana. App. 3(1997)5