Polarisationsidentität

Dieser Artikel wurde auf der Qualitätssicherungsseite des Portals Mathematik eingetragen. Dies geschieht, um die Qualität der Artikel aus dem Themengebiet Mathematik auf ein akzeptables Niveau zu bringen. Dabei werden Artikel gelöscht, die nicht signifikant verbessert werden können. Bitte hilf mit, die Mängel dieses Artikels zu beseitigen, und beteilige dich bitte an der Diskussion!

Eine quadratische Form ist in der Mathematik eine Funktion, die sich in einigen Aspekten wie 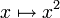$x\mapsto x^2$ verhält. Das bekannteste Beispiel ist das Quadrat des Betrages eines Vektors. Quadratische Formen tauchen in vielen Bereichen der Mathematik auf. In der Geometrie dienen quadratische Formen dazu Metriken einzuführen und in der Elementargeometrie zur Beschreibung von Kegelschnitten. Sie sind aber, falls z. B. über den rationalen oder ganzen Zahlen betrachtet, auch ein klassischer Gegenstand der Zahlentheorie, in der man z. B. nach den Zahlen fragt, die sich durch eine quadratische Form darstellen lassen. Hier werden im Folgenden vor allem zahlentheoretische Aspekte betrachtet.

Motivation

Ein (reeller) Vektorraum V mit Skalarprodukt 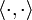$\langle\cdot,\cdot\rangle$ lässt sich zu einem normierten Raum machen, indem man die Norm eines Vektors x durch 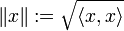$\|x\|:=\sqrt{\langle x,x\rangle}$ definiert. Die hierbei verwendete Quadratwurzel stört insofern, als man, wenn man stattdessen die Abbildung 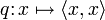$q\colon x\mapsto \langle x,x\rangle$ betrachtet, auch auf allgemeinere Bilinearformen und andere Grundkörper K verallgemeinern kann. Da ein Vektorraum dadurch bestimmt ist, dass Vektoren addiert und mit Elementen des Grundkörpers skaliert werden können, ist zu untersuchen, wie die Abbildung q sich hierbei verhält. Man findet die folgenden Beziehungen:

• q(ax) = a²q(x) für alle 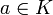$a\in K$ und $x\in V$
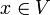
• q(x + y) + q(x − y) = 2q(x) + 2q(y) für alle $x,y\in V$

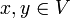
Abbildungen 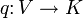$q\colon V\to K$, die die obigen Bedingungen erfüllen, kann man auch betrachten, ohne dass sie von einer Biliniearform herstammen. Obendrein kann man von Vektorräumen über einem Körper zu Moduln über einem kommutativen Ring mit Einselement verallgemeinern. Häufig untersucht man hierbei den Ring 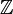$\Z$ der ganzen Zahlen sowie den Modul 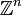$\Z^n$, insb. $\Z^2$.

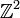Definition

Eine quadratische Form (in n Unbestimmten) über einem kommutativen Ring mit Einselement A ist ein homogenes Polynom vom Grad 2 in n Unbestimmten mit Koeffizienten in A.

Der Begriff Form wurde von Legendre geprägt ^[1].

Spezialfälle

• Für n = 2 spricht man von binären quadratischen Formen. Eine binäre quadratische Form ist also ein Polynom der Gestalt aX² + bXY + cY² mit $a,b,c\in A$.

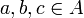• Für n = 3 spricht man von ternären quadratischen Formen. Eine ternäre quadratische Form ist also ein Polynom der Gestalt aX² + bXY + cXZ + dY² + eYZ + fZ² mit $a,\ldots,f\in A$.

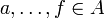Algebraische Voraussetzungen

Im folgenden sei angenommen, dass 2 in dem Ring A invertierbar ist. Dies gilt insbesondere für Körper der Charakteristik ungleich 2 wie den reellen oder komplexen Zahlen.

Ordnet man einer quadratischen Form 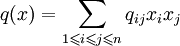$q(x) = \sum_{1 \leqslant i \leqslant j \leqslant n} q_{ij}x_ix_j$ die Dreiecksmatrix Q = (q_ij wenn 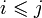$i \leqslant j$, sonst 0) zu, so kann man q(x) auch als Matrixprodukt x^TQx bzw. x^TQ^Tx auffassen. Hieraus ergibt sich zunächst:

• Bezug zu symmetrischen Bilinearformen

Es gibt eine eineindeutige Entsprechung zwischen quadratischen Formen in n Unbestimmten und symmetrischen Bilinearformen auf Aⁿ:

Zu einer quadratischen Form q erhält man eine symmetrische Bilinearform B durch Polarisierung

$B(x,y) = \frac{1}{2}(q(x+y) - q(x) - q(y))$.

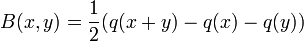Umgekehrt ist q(x) = B(x,x).

(Formal gesehen liefert diese Konstruktion zunächst nur eine Polynomfunktion; man erhält aber tatsächlich ein Polynom, indem man die Bilinearform durch eine Matrix darstellt oder sie auf beliebige A-Algebren ausdehnt.)

• Äquivalenz von Formen

Wenn S eine n-reihige Matrix ist, dann erhält man durch die Substitution y = Sx eine neue quadratische Form y^T(S^TQS)y. Wenn S invertierbar ist, kann man aus der neuen Form auch wieder die alte Form rückgewinnen. Insgesamt ermöglicht so eine Matrixgruppe Γ die Einführung einer Äquivalenzrelation auf der Menge aller quadratischen Formen. Wir sprechen hier von Γ-äquivalenten Formen (Beachte auch die Schlussbemerkung zu 4).

• Definitheit

Für reelle oder rationale Formen kann man über die entsprechenden Matrixkriterien für Q + Q^T (Definitheit) Aussagen darüber gewinnen, ob der Wertebereich der Form über $\mathbb{R}^n$ nur positive oder nur negativen Werte annimmt, oder ob eine derartige Beschränkung nicht zutrifft. Entsprechend wird die Form positiv definit, negativ definit oder indefinit genannt.

Fragestellungen diophantischer Natur

Zur Frage, ob eine vorgegebene ganzzahlige quadratische Form mit irgendwelchen ganzzahligen Argumenten einen vorgegebenen Wert annehmen kann („einen Wert darstellt bzw repräsentiert“), gibt es eine Vielzahl von Ergebnissen. Für sich betrachtet haben diese Ergebnisse naturgemäß oft anekdotischen Charakter. Beachtet man jedoch, dass

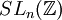• $SL_n(\mathbb{Z})$, die Gruppe der n-reihigen, ganzzahligen Matrizen der Determinante 1, und
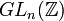• $GL_n(\mathbb{Z})$, die Gruppe der n-reihigen, ganzzahligen Matrizen der Determinante ±1,

jeweils sowohl das Gitter 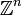$\mathbb{Z}^n$ als auch die Menge der teilerfremden Zahlen in 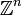$\mathbb{Z}^n$ bijektiv auf sich abbildet, so stehen wegen (2.2) die folgenden Ergebnisse jeweils für ganze Familien äquivalenter Formen.

Prominent sind beispielsweise die folgenden Themen

• Quadratzahlen der Form x² + y²

Die ganzzahligen Lösungen der Gleichung x² + y² = z² heißen Pythagoräische Zahlen. Die bekannteste Lösung dieser Aufgabe ist 3² + 4² = 5². Dies ist die kleinste einer unendlichen Anzahl von Lösungen.

Mehr als die übliche parametrische Beschreibung aller Lösungen (Pythagoreisches Tripel) findet sich in ^[2]. In ^[3] eine ganze Reihe weiterer Literaturhinweise.

• Zahlen der Form w² + x² + y² + z²

Der erste bekannte Fall (Lagrange 1770) einer quadratischen Form, die alle natürlichen Zahlen darstellt.

Ein Beweis in ^[4], Abschnitt 17.7. Weiterführende Informationen zum Thema quadratischer Formen, die alle natürlichen Zahlen darstellen, via 15 theorem.

• ganzzahlige Lösungen der Gleichung ax² + by² + cz² = 0

(a,b,c ganzzahlig, paarweise teilerfremd, nicht alle vom gleichen Vorzeichen).

Die Gleichung ist genau dann lösbar, wenn − ab(mod c), − bc(mod a) und − ca(mod b) quadratische Reste im jeweiligen Modul sind. Ein Ergebnis von Legendre, siehe ^[4], Theorem 17.3.1

(für die Notation siehe Kongruenz (Zahlentheorie))

• Primzahlen der Form x² + y²

Dies sind genau die Primzahlen 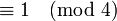$\equiv 1 \pmod4$. Die Beobachtung ist historisch von besonderer Bedeutung, sie geht auf Fermat zurück.

Ein moderner Beweis, geradezu die Mutter aller Beweise, in ^[5], Kapitel 4.

• Primzahlen der Form x² + xy + y²

Dies sind genau die Primzahlen, die 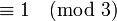$\equiv1\pmod3$ sind.^[6]

• Primzahlen der Form x² + ny²

Mit dieser Fragestellung befasst sich das äußerst reichhaltige Buch von Cox (^[1]).

Verwandte Fragestellungen, allerdings außerhalb des Bereichs der quadratischen Formen, sind Themen wie der Satz von Fermat und das Waring Problem.

Verwandte Begriffe

Die (projektive) Nullstellenmenge einer quadratischen Form wird als Quadrik bezeichnet.

Einzelnachweise

1. ↑ ^{a b} David Cox, Primes of the form x² + ny². Wiley & Sons, 1997, Seite 40.
2. ↑ Roger C. Alperin, The modular tree of Pythagorus.
3. ↑ Dan Romik, The dynamics of Pythagorean triples.
4. ↑ ^{a b} Kenneth Ireland, Michael Rosen, A Classical Introduction to Modern Number Theory. Springer-Verlag, 1982
5. ↑ Martin Aigner, Günter M. Ziegler, Proofs from the Book. Springer-Verlag, 2000
6. ↑ G. H. Hardy, E. M. Wright, An Introduction to the Theory of Numbers, 4. Auflage, Oxford University Press, Oxford 1975. ISBN 0-19-853310-1: Theorem 366, S. 299; Theorem 254, S. 221

Literatur

• Martin Kneser, Rudolf Scharlau: Quadratische Formen, 1. Aufl., Springer, Berlin 2002, ISBN 3-540-64650-7

Weblinks

• Springer Encyclopaedia of Mathematics: Quadratic form
• Springer Encyclopaedia of Mathematics: binary quadratic form