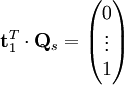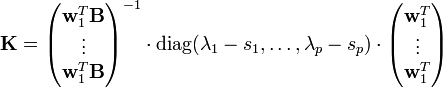- Polzuweisung
-
Die Polvorgabe bzw. Eigenwertvorgabe ist eine geradlinige Methode, einen Regler im Zustandsraum zu entwerfen. Sie besteht aus drei Schritten, die ggf. mehrfach wiederholt werden können:
- Vorgabe der Eigenwerte bzw. Pole des geschlossenen Regelkreises
- Berechnung der Zustandsrückführung
- Überprüfung, ob das Einschwingverhalten / Stellgrößenverlauf das gewünschte Verhalten haben
Grundlage für dieses Vorgehen ist der enge Zusammenhang zwischen den Eigenwerten eines Systems (hier des geschlossenen Regelkreises) und seiner Sprungantwort.
Besonders einfach wird das Verfahren beim Entwurf von vollständigen Zustandsrückführungen für Eingrößensystemen, da hier in der Regel eine eindeutige Rückführung existiert. Sie kann mit der sog. Formel von Jürgen Ackermann ermittelt werden. Für Systeme mit mehr als einer Stellgröße (Mehrgrößensysteme) existieren die Verfahren der modalen Polvorgabe und die Entkopplung nach Falb-Wolovich.
Wenn nicht alle Zustandsgrößen messbar sind, können die nicht messbaren Größen durch einen Beobachter aus den messbaren Größen berechnet werden.
Beim Entwurf von Ausgangsrückführungen werden nicht alle Zustandsgrößen zurückgeführt. Dies ist der Fall, wenn einerseits nicht alle Zustandsgrößen messbar sind, anderseits aber ein Beobachter nicht eingesetzt werden kann. Hier ist man auf numerische Methoden angewiesen.[FOE94 1]
Ein anderer Weg zum Entwurf von Zustandsreglern ist die Optimale Regelung.
Inhaltsverzeichnis
Vorgabe der Pole
Zur Wahl der Pole bzw. Eigenwerte des Regelung lässt sich keine generelle Vorgehensweise angeben. Natürlich müssen alle Pole links der Imaginärachse liegen um die Stabilität zu sichern. Zu weit links wird man sie nicht legen können, da dies bei realen Systemen in die Stellgrößenbeschränkung führt.[FOE94 2]
Bestimmung der Reglerparameter
Das System sei im Zustandsraum durch
beschrieben und es soll eine Rückführung
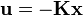 .
.
bestimmt werden. Dann wird der geschlossene Regelkreis durch
beschrieben. Die Eigenwerte des geschlossenen Regelkreises sind die Lösung si der Gleichung
Das Wesen der Polvorgabe besteht nun darin, die Elemente von
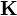 so zu bestimmen, dass
so zu bestimmen, dassgilt. Die si sind dabei die Sollpole des geschlossenen Regelkreises.
Ist n die Systemordnung so führt ein Koeffizientenvergleich zu n Gleichungen. Bei Eingrößensystemen stehen diesen die n Elemente des Zeilenvektors
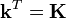 gegenüber. Ist das System steuerbar, so kann eine eindeutige Lösung angegeben werden. Bei Mehrgrößensystemen mit p Stellgrößen sind
gegenüber. Ist das System steuerbar, so kann eine eindeutige Lösung angegeben werden. Bei Mehrgrößensystemen mit p Stellgrößen sind 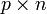 Elemente von
Elemente von 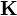 zu bestimmen, d.h. das Gleichungssystem ist unterbestimmt. Anderseits sind die Gleichungen nichtlinear, so dass keine allgemeine Lösung angegeben werden kann. Die Verfahren der Modalen Regelung und der Entkopplung nach Falb-Wolovich schränken den Lösungsraum derart ein, dass eine Lösung angegeben werden kann. [FOE94 3]
zu bestimmen, d.h. das Gleichungssystem ist unterbestimmt. Anderseits sind die Gleichungen nichtlinear, so dass keine allgemeine Lösung angegeben werden kann. Die Verfahren der Modalen Regelung und der Entkopplung nach Falb-Wolovich schränken den Lösungsraum derart ein, dass eine Lösung angegeben werden kann. [FOE94 3]Polvorgabe bei Eingrößensystemen
Die Reglerparameter bestimmen sich nach der Formel von Ackermann in folgender Weise:
Es sei
das gewünschte charakteristische Polynom des geschlossenen Regelkreises. Dann bestimmt sich die Reglermatrix nach
Dabei ist
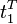 die letzte Zeile der inversen Steuerbarkeitsmatrix
die letzte Zeile der inversen Steuerbarkeitsmatrix[FOE94 4] Damit ist auch der Zusammenhang zwischen der Polvorgabe und der dazu notwendigen Bedingung der Steuerbarkeit offensichtlich. Tatsächlich wird man natürlich nicht
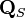 invertieren sondern das lineare Gleichungssystem
invertieren sondern das lineare Gleichungssystemlösen.
Nach [FOE94 5] wurde dieser Zusammenhang erstmalig in [1] angegeben.
Die Verbindung dieser Entwurfsformel mit dem Namen Jürgen Ackermann findet sich z.B. in [FOE94 5]
Polvorgabe bei Mehrgrößensystemen
Modale Regelung
Die modale Regelung erlaubt die Verschiebung von p Eigenwerten, wobei p die Anzahl der Stellgrößen ist. Durch mehrfaches Durchführen können aber auch letztlich alle Pole verschoben werden. Die Reglermatrix bestimmt sich nach
Dabei sind
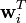 die sog. Linkseigenvektoren also die Zeilen der Inversen der Eigenvektormatrix der Systemmatrix
die sog. Linkseigenvektoren also die Zeilen der Inversen der Eigenvektormatrix der Systemmatrix 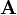 , λi die Eigenwerte des Systems und si die Solleigenwerte.
, λi die Eigenwerte des Systems und si die Solleigenwerte.Die nicht gezielt verschobenen Eigenwerte bleiben bei diesem Entwurfsverfahren unverändert. Sollen diese auch verschoben werden, so ist dass Verfahren abermals auf den geschlossen (inneren) Regelkreis anzuwenden. [FOE94 6]
Nach [FOE94 6] stammt das Verfahren von H.H. Rosenbrock (1962) [2]
Entkopplung nach Falb-Wolovich
Ziel der Entkopplung nach Falb-Wolovich ist ein Führungsverhalten, bei der eine Änderung einer Führungsgröße auch nur die dazugehörige Regelgröße beeinflusst.
Nach [FOE94 7] wird er in [3] vorgestellt. Es lässt sich auf auf zeitvariante und nichtlineare Systeme erweitern. Für Details sei auf [FOE94 7] verwiesen.
Literatur und Einzelnachweise
Grundlage des Artikels ist Otto Föllinger: Regelungstechnik, Einführung in die Methoden und ihre Anwendung. 8. Auflage. Hüthig Verlag, Heidelberg 1994, ISBN 3-7785-2336-8.
- ↑ Abschnitt 14
- ↑ Abschnitt 13.3.1
- ↑ Abschnitt 13.3.3, 13.5
- ↑ Abschnitt 13.3.2 Formel (13.32)
- ↑ a b Abschnitt 13.3.2
- ↑ a b Abschnitt 13.3.3
- ↑ a b Abschnitt 13.5
Dieser zitiert folgende Einzelartikel, die aus geschichtlichen Gründen angegeben werden
- ↑ J. Ackermann: Der Entwurf linearer Regelungssysteme im Zustandsraum. Regelungstechnik 20 (1972), S. 297-300
- ↑ H.H. Rosenbrock: Distinctive Problems of Process Control. Chemical Engineering Progress 58 ( 1962), S.43-50
- ↑ P. L. Falb - W. A. Wolovich: Decoupling in the Design and Synthesis of Multivariable Control Systems. IEEE Trans. on Automatic Control 12 (1967), S.651-659
Wikimedia Foundation.

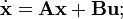
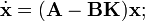
![\det\left[s\mathbf{I}-\left(\mathbf{A}-\mathbf{B}\mathbf{K}\right)\right]=0](/pictures/dewiki/56/81ce539c2ab20eadbeabe0db8acfdea2.png)
![\det\left[s\mathbf{I}-\left(\mathbf{A}-\mathbf{B}\mathbf{K}\right)\right]=\prod_{i=1}^n (s-s_i)](/pictures/dewiki/50/2be1d09d17ef83f9fbc9ed1e767b86c5.png)
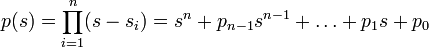
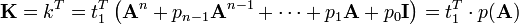
![\mathbf{Q}_S^{-1} = \left[\mathbf{b}, \mathbf{A}\mathbf{b},\dots ,\mathbf{A}^{n-1}\mathbf{b}\right]^{-1}](/pictures/dewiki/51/31eb54cc276979ab747c791b071b1e3c.png)