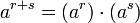Potenz-assoziative Algebra — Eine potenz assoziative Algebra ist eine Algebra, in welcher die Potenzen eines Elements unabhängig von der Beklammerungsreihenfolge definiert werden können. Definition Für eine Algebra und jedes definiere man a1: = a sowie für jedes . Die… … Deutsch Wikipedia
Assoziativ-Gesetz — Das Assoziativgesetz (lat. associare vereinigen, verbinden, verknüpfen, vernetzen), auf Deutsch Verknüpfungsgesetz oder auch Verbindungsgesetz, ist eine Regel aus der Mathematik. Eine (zweistellige) Verknüpfung ist assoziativ, wenn die… … Deutsch Wikipedia
Potenz (Mathematik) — Das Potenzieren (von lat. potentia, ‚Vermögen, Macht‘, als Lehnübersetzung aus gr. δύναμις, das in der antiken Geometrie spätestens seit Platon auch die Bedeutung ‚Quadrat‘ hatte) ist wie das Multiplizieren seinem Ursprung nach eine… … Deutsch Wikipedia
Potenz (Wort) — In der theoretischen Informatik ist ein Wort eine endliche Folge von Symbolen (Zeichenkette) aus einem Alphabet. Die Anzahl der Symbole eines Wortes w ist ihre Länge und wird mit | w | bezeichnet. Ein besonderes Wort ist das leere Wort, welches… … Deutsch Wikipedia
Potenz (Formale Sprache) — Die Artikel Formale Sprache, Formales System, Formales System (Logik) und Kalkül überschneiden sich thematisch. Hilf mit, die Artikel besser voneinander abzugrenzen oder zu vereinigen. Beteilige dich dazu an der Diskussion über diese… … Deutsch Wikipedia
Sedenionen — Die Sedenionen (Symbol ) sind 16 dimensionale hyperkomplexe Zahlen. Sie entstehen durch die Anwendung des Verdopplungsverfahrens aus den Oktonionen. Die Multiplikation der Sedenionen ist weder kommutativ noch assoziativ und ist auch nicht… … Deutsch Wikipedia
Verdopplungsverfahren — Das Verdopplungsverfahren, auch als Cayley Dickson Verfahren bekannt, ist ein Verfahren zur Erzeugung hyperkomplexer Zahlen. Das neue Zahlensystem hat dabei doppelt so viele Dimensionen wie das Ausgangssystem. Die Bedeutung des… … Deutsch Wikipedia
Assolziativität — Das Assoziativgesetz (lat. associare vereinigen, verbinden, verknüpfen, vernetzen), auf Deutsch Verknüpfungsgesetz oder auch Verbindungsgesetz, ist eine Regel aus der Mathematik. Eine (zweistellige) Verknüpfung ist assoziativ, wenn die… … Deutsch Wikipedia
Assoziative Verknüpfung — Das Assoziativgesetz (lat. associare vereinigen, verbinden, verknüpfen, vernetzen), auf Deutsch Verknüpfungsgesetz oder auch Verbindungsgesetz, ist eine Regel aus der Mathematik. Eine (zweistellige) Verknüpfung ist assoziativ, wenn die… … Deutsch Wikipedia
Assoziativität — Das Assoziativgesetz (lat. associare vereinigen, verbinden, verknüpfen, vernetzen), auf Deutsch Verknüpfungsgesetz oder auch Verbindungsgesetz, ist eine Regel aus der Mathematik. Eine (zweistellige) Verknüpfung ist assoziativ, wenn die… … Deutsch Wikipedia
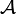 und jedes
und jedes  definiere man
definiere man für jedes
für jedes 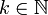 .
.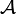 heißt potenz-assoziativ, wenn für alle
heißt potenz-assoziativ, wenn für alle  und alle natürlichen Zahlen
und alle natürlichen Zahlen  (null wird hier nicht als natürliche Zahl angesehen) gilt
(null wird hier nicht als natürliche Zahl angesehen) gilt ein
ein  gibt mit
gibt mit  , sind potenz-assoziativ.
, sind potenz-assoziativ.
 , ausgestattet mit dem Kreuzprodukt, da
, ausgestattet mit dem Kreuzprodukt, da  für alle
für alle 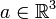 .
.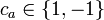 .
.