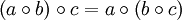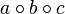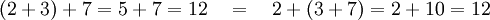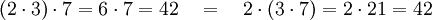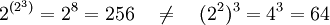Assoziativ-Gesetz

Das Assoziativgesetz (lat. associare - vereinigen, verbinden, verknüpfen, vernetzen), auf Deutsch Verknüpfungsgesetz oder auch Verbindungsgesetz, ist eine Regel aus der Mathematik. Eine (zweistellige) Verknüpfung ist assoziativ, wenn die Reihenfolge der Ausführung keine Rolle spielt. Anders gesagt: Die Klammerung mehrerer assoziativer Verknüpfungen ist beliebig.

Definition

Assoziativgesetz = Klammergesetz

In einem Summen- oder Produktterm darf man die Summanden oder Faktoren beliebig mit Klammern verbinden. Dies gilt auch für mehr als drei Summanden oder Faktoren.

Eine binäre Verknüpfung 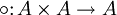${\circ}\colon A \times A\to A$ auf einer Menge A heißt assoziativ, wenn für alle 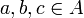$a,b,c\in A$ gilt

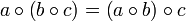$a \circ \left( b \circ c \right) = \left( a \circ b \right) \circ c$ (Assoziativität)

Folgerungen

Bei Gültigkeit des Assoziativgesetzes lässt sich eine vereinfachte klammerfreie Notation einführen. Wegen

$\left( a \circ b \right) \circ c = a \circ \left( b \circ c \right)$

ist der Ausdruck

$a \circ b \circ c$

eindeutig, da aus jeder beliebigen Klammerung immer das gleiche Ergebnis folgt.

Beispiele

Als Verknüpfungen auf den reellen Zahlen sind Addition und Multiplikation assoziativ, es gilt zum Beispiel Addition:

$(2+3)+7=5+7=12\quad =\quad 2+(3+7)=2+10=12$

Multiplikation:

$(2\cdot 3)\cdot 7=6\cdot 7=42\quad =\quad 2\cdot (3\cdot 7)=2\cdot 21=42$

Die Subtraktion und Division sind hingegen nicht assoziativ, denn es ist z. B. Subtraktion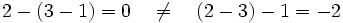

$2 - (3 - 1) = 0 \quad\neq\quad (2 - 3) - 1 = -2$.

Division:

$(4/2)/2 = 1 \quad\neq\quad 4/(2/2)= 4$.

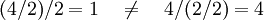Auch die Potenz ist nicht assoziativ, da z. B.

$2^{(2^3)} = 2^8 = 256 \quad\neq\quad (2^2)^3 = 4^3 = 64$

gilt.

Einordnung

Das Assoziativgesetz gehört zu den Gruppenaxiomen, wird aber bereits für die schwächere Struktur einer Halbgruppe gefordert.

Siehe auch

• Alternativität
• Distributivgesetz
• Flexibilitätsgesetz
• Kommutativgesetz
• Algebra
• Operatorassoziativität

Literatur

Otto Forster: Analysis 1: Differential- und Integralrechnung einer Veränderlichen. Vieweg-Verlag, München 2008, ISBN 978-3-8348-0395-5.