Potenzglatt

Eine glatte Zahl bezüglich einer Schranke S ist eine natürliche Zahl, in deren Primfaktorzerlegung keine Primzahlen vorkommen, die größer als die Schranke sind. Man bezeichnet eine solche Zahl auch als S-glatt. Beispielsweise ist die Zahl 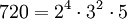$720 = 2^4 \cdot 3^2 \cdot 5$ eine 5-glatte Zahl.

Eine natürliche Zahl heißt potenzglatt bezüglich einer Schranke S, wenn in ihrer Primfaktorzerlegung nur Primpotenzen kleiner oder gleich S vorkommen. Das heißt, für einen Primfaktor q, der a mal vorkommt gilt:

$q^a \leq S$.

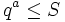Das Quadratische Sieb, ein Faktorisierungsverfahren, beruht auf der Primfaktorzerlegung Quadratischer Reste. Diese Zerlegung kann für glatte Zahlen leicht durchgeführt werden.

Folgen glatter Zahlen

Für jede Schranke S bilden die entsprechenden S-glatten Zahlen eine Folge. Unter der On-Line Encyclopedia of Integer Sequences stehen diese Folgen für kleine Schranken zur Verfügung:

• 2-glatte Zahlen: Folge A000079 in OEIS – alle Zweierpotenzen
• 3-glatte Zahlen: Folge A003586 in OEIS – Zahlen der Form $2^x \cdot 3^y$
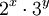
• 5-glatte Zahlen: Folge A051037 in OEIS – Zahlen der Form $2^x \cdot 3^y \cdot 5^z$
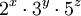
• 7-glatte Zahlen: Folge A002473 in OEIS
• 11-glatte Zahlen: Folge A51038 in OEIS
• 13-glatte Zahlen: Folge A80197 in OEIS
• 17-glatte Zahlen: Folge A80681 in OEIS
• 19-glatte Zahlen: Folge A80682 in OEIS
• 23-glatte Zahlen: Folge A80683 in OEIS