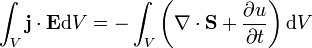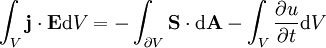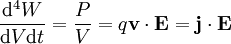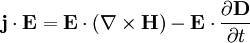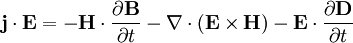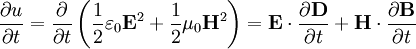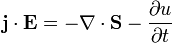Poynting-Satz

Der Satz von Poynting stellt einen Erhaltungssatz in der Elektrodynamik dar. Damit wird der Energieerhaltungssatz auf elektromagnetische Felder verallgemeinert. Seine Formulierung wird dem britischen Physiker John Henry Poynting zugeschrieben. Stark vereinfacht trägt er in sich die Aussage, dass ein elektromagnetisches Feld Arbeit verrichten kann, wenn es dabei „schwächer“ wird. Mathematisch kann er, wie auch die Maxwellschen Gleichungen, sowohl in einer differenziellen als auch in einer integralen Schreibweise angegeben werden. In seiner integralen Form lautet er:

$\int_V \mathbf{j} \cdot \mathbf{E}\mathrm{d}V=-\int_V \left( \nabla \cdot \mathbf{S}+\frac{\partial u}{\partial t} \right) \mathrm{d}V$

Wobei:

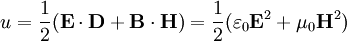$u=\frac{1}{2}(\mathbf{E}\cdot\mathbf{D} + \mathbf{B}\cdot\mathbf{H}) = \frac{1}{2}(\varepsilon_0\mathbf{E}^2 + \mu_0\mathbf{H}^2)$ elektromagnetische Energiedichte der Felder im Vakuum.

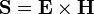$\mathbf{S}=\mathbf{E} \times \mathbf{H}$ Poynting-Vektor

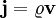$\mathbf{j}=\varrho \mathbf{v}$ Stromdichte

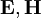$\mathbf{E},\mathbf{H}$ elektrische und magnetische Feldstärken

Er besagt, dass die Leistung eines Feldes gleich dem Austritt des Energiestromes und der Abnahme der Feldenergie ist. Damit ist er vergleichbar mit dem Energieerhaltungssatz. Das kann man sich klar machen, wenn man den Gaußschen Satz in der Integralform anwendet:

$\int_V \mathbf{j} \cdot \mathbf{E}\mathrm{d}V=-\int_{\partial V} \mathbf{S} \cdot \mathrm{d}\mathbf{A}-\int_V \frac{\partial u}{\partial t}\mathrm{d}V$

Das Oberflächenintegral entspricht dann dem Fluss der Leistungsdichte durch die betrachtete Oberfläche des Volumens V.

Da nur die Divergenz von 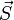$\vec{S}$ relevant ist, könnte prinzipiell auch eine Rotation einer beliebigen Funktion zu ihm hinzugefügt werden, da sie unter der Einwirkung der Divergenz verschwindet. Die physikalische Interpretation von 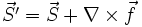$\vec{S'}=\vec{S}+\nabla \times \vec{f}$ als Leistungsfluss ist dann allerdings nicht mehr möglich. Es gibt also formal unendlich viele vektorwertige Funktionen, die den Satz von Poynting erfüllen, aber nur 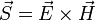$\vec{S}=\vec{E} \times \vec{H}$ lässt sich aus den Maxwell-Gleichungen gewinnen und ist damit physikalisch sinnvoll.

Herleitung

Ausgangspunkt ist die Arbeit, die ein elektromagnetisches Feld an Ladungsträgern pro Zeit und Volumen verrichtet:

$\frac{\mathrm{d}^4 W}{\mathrm{d}V\mathrm{d}t}=\frac{P}{V}=q \mathbf{v} \cdot \mathbf{E}=\mathbf{j} \cdot \mathbf{E}$

Es bleibt anzumerken, dass der magnetische Teil des Feldes keine Arbeit verrichet, da die Lorentzkraft senkrecht zu Bewegungsrichtung der Ladung wirkt. Nun gilt aber das Durchflutungsgesetz: 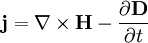$\mathbf{j}=\nabla \times \mathbf{H}-\frac{\partial \mathbf{D}}{\partial t}$. Was oben eingesetzt auf

$\mathbf{j} \cdot \mathbf{E}=\mathbf{E} \cdot (\nabla \times \mathbf{H})-\mathbf{E} \cdot \frac{\partial \mathbf{D}}{\partial t}$

führt. Zieht man daneben noch die Rechenregel für die Divergenz

$\nabla \cdot (\mathbf{E}\times\mathbf{H})=\mathbf{H} \cdot (\nabla\times\mathbf{E})-\mathbf{E} \cdot (\nabla\times\mathbf{H})$

heran, so ergibt sich

$\mathbf{j} \cdot \mathbf{E}=\mathbf{H} \cdot (\nabla\times\mathbf{E})-\nabla \cdot (\mathbf{E}\times\mathbf{H})-\mathbf{E} \cdot \frac{\partial \mathbf{D}}{\partial t}$.

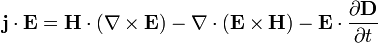Die Rotation des elektrischen Feldes kann schließlich über das Induktionsgesetz 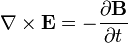$\nabla \times \mathbf{E}=-\frac{\partial \mathbf{B}}{\partial t}$ ausgedrückt werden, womit wir bei

$\mathbf{j} \cdot \mathbf{E}=-\mathbf{H} \cdot \frac{\partial \mathbf{B}}{\partial t}-\nabla \cdot (\mathbf{E}\times\mathbf{H})-\mathbf{E} \cdot \frac{\partial \mathbf{D}}{\partial t}$

ankämen. Hier bleibt es nur noch mit Hilfe der Definition des Poynting-Vektors und der Energiedichte die Gleichung zusammenzufassen, wozu noch die folgenden Identitäten benötigt werden:

$\mathbf{D}=\varepsilon_0\mathbf{E} \qquad \mathbf{B}=\mu_0\mathbf{H}$

und

$\frac{\partial u}{\partial t}=\frac{\partial }{\partial t} \left(\frac{1}{2}\varepsilon_0\mathbf{E}^2+\frac{1}{2}\mu_0\mathbf{H}^2 \right)=\mathbf{E} \cdot \frac{\partial \mathbf{D}}{\partial t}+\mathbf{H} \cdot \frac{\partial \mathbf{B}}{\partial t}$

Womit schließlich die differenzielle Form das Satzes gerechtfertigt wäre.

$\mathbf{j} \cdot \mathbf{E}=-\nabla \cdot \mathbf{S}-\frac{\partial u}{\partial t}$

Literatur

• John David Jackson: Klassische Elektrodynamik. 4., überarbeitete Auflage. de Gruyter, Berlin 2006, ISBN 3-11-018970-4