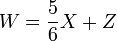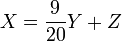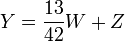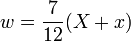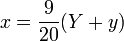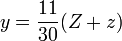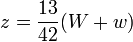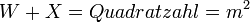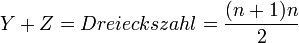- Problema Bovinum
-
Das Rinderproblem des Archimedes, auch Problema Bovinum, ist ein zahlentheoretisches Problem aus der Theorie Diophantischer Gleichungen, das heißt Polynomgleichungen über den ganzen Zahlen. Das Problem wird Archimedes zugeschrieben: Die Anzahl der Rinder (Bullen und Kühe, mit je vier Sorten) in einer Herde des Sonnengottes soll bestimmt werden aus einigen Nebenbedingungen.
Inhaltsverzeichnis
Geschichte
Das Problem wurde 1773 von Gotthold Ephraim Lessing in einem griechischem Manuskript der Herzog August Bibliothek in Wolfenbüttel entdeckt, das einen in 44 Distichen abgefassten Brief des Archimedes an Eratosthenes von Kyrene enthielt (also aus Syrakus nach Alexandria).
Ob der Brief tatsächlich von Archimedes stammt wird von Lessing und anderen angezweifelt, das Problem selbst ist aufgrund seiner Schwierigkeit jedoch möglicherweise auf Archimedes zurückzuführen (so zum Beispiel die Sicht von B. Krumbiegel[1]). Ein Hinweis darauf ist auch Archimedes Interesse an großen Zahlen, wie sie etwa in Der Sandrechner zum Vorschein kommt.
Eine deutsche Übertragung des Gedichts wurde 1842 von G. H. F. Nesselmann angefertigt und veröffentlicht, eine weitere von B. Krumbiegel 1880. Eine philologische Version des griechischen Texts und eine Übersetzung ins Lateinische findet sich im zweiten Band der von Johan Ludvig Heiberg besorgten Ausgabe der Werke von Archimedes.[2]
Der von Lessing veröffentlichte Text enthält eine Teillösung, die aber zwei Forderungen aus dem zweiten Teil des Gedichtes nicht erfüllt. Dies blieb wegen der zur Lösung nötigen Berechnung von sehr großen Zahlen bis vor einigen Jahren ungelöst. Ein Lösungsverfahren wurde 1880 von A. Amthor gefunden. Er fand, dass die genaue Lösung in Exponentialdarstellung etwa
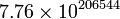 Rinder lautet (das heißt eine Dezimalzahl mit 206.544 Stellen). Die Dezimaldarstellung der Lösung wurde erst 1965 unter Verwendung von Computern (IBM 7040 und IBM 1620) von H. C. Williams, R. A. German and C. R. Zarnke explizit angegeben.[3]. Die Computer brauchten damals dafür 7 Stunden 49 Minuten.
Rinder lautet (das heißt eine Dezimalzahl mit 206.544 Stellen). Die Dezimaldarstellung der Lösung wurde erst 1965 unter Verwendung von Computern (IBM 7040 und IBM 1620) von H. C. Williams, R. A. German and C. R. Zarnke explizit angegeben.[3]. Die Computer brauchten damals dafür 7 Stunden 49 Minuten.Problem
Das Problem, in einer an Nesselmann und Krumbiegel angelehnten, das Versmaß nicht erhaltenden vereinfachten Fassung:
Zähle, mein Freund, die Rinder unter der Sonne, die einst unter der Sonne Siziliens grasten, die nach ihrer Farbe in vier Herden geteilt werden. Eine ist milchweiß, eine schwarz, eine gefleckt und eine gelb. Die Anzahl der Bullen ist größer als die der Kühe, und die Beziehung zwischen ihnen ist wie folgt:
- weiße Bullen
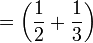 schwarze Bullen + gelbe Bullen,
schwarze Bullen + gelbe Bullen, - schwarze Bullen
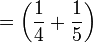 gefleckte Bullen + gelbe Bullen,
gefleckte Bullen + gelbe Bullen, - gefleckte Bullen
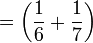 weiße Bullen + gelbe Bullen,
weiße Bullen + gelbe Bullen, - weiße Kühe
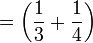 schwarze Herde,
schwarze Herde, - schwarze Kühe
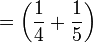 gefleckte Herde,
gefleckte Herde, - gefleckte Kühe
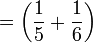 gelbe Herde,
gelbe Herde, - gelbe Kühe
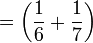 weiße Herde.
weiße Herde.
- Weiße Bullen + schwarze Bullen = eine quadratische Zahl,
- Gefleckte Bullen + gelbe Bullen = eine Dreieckszahl.
In Gleichungsform formuliert: Gesucht werden die Anzahlen W,X,Y,Z verschieden gefärbter Bullen und w,x,y,z von Kühen in den entsprechenden Farben mit:
Die Gesamtzahl der Rinder ist dann W + X + Y + Z + w + x + y + z.
In der schwierigeren Form werden zusätzlich die Nebenbedingungen:
verlangt (für ganze Zahlen n,m).
Einzelnachweise
- ↑ B. Krumbiegel, A. Amthor: Das Problema bovinum des Archimedes. In: Zeitschrift für Mathematik und Physik, Hist.-lit. Abt. Band 25 (1880) 121–136 und 153–171
- ↑ I. L. Heiberg (Hrsg.): Archimedes, Opera Omnia (Bibliotheca Scriptorum Graecorum et Romanorum Teubneriana). Teubner, Stuttgart 1972, Nachdruck der Ausgabe von 1913.
- ↑ H. C. Williams, R. A. German, C. R. Zarnke: Solution of the cattle problem of Archimedes. In: Mathematics of Computation, Band 19, 1965, S. 671–674
- ↑ Merriman, Mansfield: The Cattle Problem of Archimedes. In: Popular Science Monthly Band 67, 1905, Seiten 660–665.
Quellen
- Peter Schreiber: A Note on the Cattle Problem of Archimedes. In: Hist. Math. Band 20, 1993, S. 304-306 (online).
- G. Nesselmann: Die Algebra der Griechen. Reimer, Berlin 1842.
Weblinks
- weiße Bullen
Wikimedia Foundation.