- Produktsymbol
-
In der Mathematik bezeichnet der Begriff Produkt eine Verknüpfung zweier Elemente. Das bekannteste Produkt ist die Multiplikation von Zahlen.
Inhaltsverzeichnis
Produkt von Zahlen
- Hauptartikel: Multiplikation
Hauptbedeutung ist das Ergebnis der Multiplikation reeller Zahlen. Man schreibt
und nennt a und b Faktoren und die rechte Seite das Produkt von a und b.
Symbolik
Analog zum Summensymbol
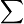 (großes Sigma) gibt es in der Mathematik das Produktsymbol
(großes Sigma) gibt es in der Mathematik das Produktsymbol 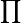 (großes Pi), um ein Produkt mehrerer Faktoren darzustellen.
(großes Pi), um ein Produkt mehrerer Faktoren darzustellen.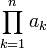 liest man als „Produkt über ak für k von 1 bis n “; der Ausdruck bedeutet
liest man als „Produkt über ak für k von 1 bis n “; der Ausdruck bedeutet 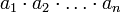 .
.- Siehe auch: Multiplikation#Produktsymbol
Produkte komplexer Zahlen
Zwei komplexe Zahlen a + bi und c + di werden wie eine Summen zweier reeller Zahlen multipliziert:
 ,
,
da i2 = − 1.
Produkte innerhalb der Quaternionen
Die Menge
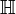 der Quaternionen entsteht, indem man zu den reellen Zahlen
der Quaternionen entsteht, indem man zu den reellen Zahlen  drei neue Zahlen i,j und k hinzufügt, wobei gilten muss:
drei neue Zahlen i,j und k hinzufügt, wobei gilten muss:- i2 = j2 = k2 = − 1.
Es gelten folgende Multiplikationsregeln für das Bilden von Produkten in der Menge der Quaternionen:
Diese beiden Regeln ergeben sich, da Quaternionen antikommutativ sind.
Eine Quaternion der Form x0 + x1i + x2j + x3k hat einen Real- oder Skalarteil
und einen Imaginär- oder Vektorteil
Aus diesem Grund ist es möglich, mithilfe des Vektor- bzw. Skalarprodukts zu rechnen. Dazu stellt man die Quaternion auch so dar:
wobei gilt:
Das Vektorprodukt aus zwei Vektorteilen der Quaternionen
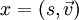 und
und 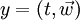 ist wie folgt definiert:
ist wie folgt definiert:Das Skalarprodukt zweier Quaternionen ist der Skalarteil von
 bzw. von
bzw. von  , wobei
, wobei 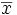 bzw.
bzw. 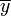 eine Konjugation ausdrückt. Es gilt also:
eine Konjugation ausdrückt. Es gilt also:Produkte von Vektoren
Es gibt zwei Arten von Produkten aus Vektoren, das Skalarprodukt und das Vektorprodukt. In beiden Fällen werden zwei Vektoren
 und
und  miteinander multipliziert.
miteinander multipliziert.Skalarprodukt
Hauptartikel: Skalarprodukt
Im Fall des Skalarprodukts (auch inneres Produkt) ist das Produkt der zwei Vektoren, die multipliziert werden, ein Skalar. Allgemein gilt:
 ,
,
wobei
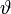 der Winkel zwischen den beiden Vektoren ist.
der Winkel zwischen den beiden Vektoren ist.Das Skalarprodukt unterliegt der Kommutativität und der Distributivität. Außerdem kann dem Skalarprodukt auch ein Betrag zugeordnet werden, da cos0 = 1. Daraus folgt:

Das Vektorprodukt
Hauptartikel: Kreuzprodukt
Das Vektor-, Kreuz- oder äußere Produkt zweier Vektoren
 und
und  ist ein weiterer Vektor
ist ein weiterer Vektor 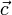 . Zur Unterscheidung vom Skalarprodukt schreibt man im Fall des Vektorprodukts:
. Zur Unterscheidung vom Skalarprodukt schreibt man im Fall des Vektorprodukts: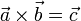 .
.
Es gilt immer:
 .
.
Der Vektor
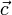 bildet mit den Vektoren
bildet mit den Vektoren  und
und  jeweils einen rechten Winkel, woraus folgt, dass das Vektorprodukt nur für den dreidimensionalen Raum definiert ist. Das Vektorprodukt ist ein so genannter axialer Vektor, da er bei einer Punktspiegelung unverändert bleibt. Das Vektorprodukt ist antikommutativ, d.h. es gilt:
jeweils einen rechten Winkel, woraus folgt, dass das Vektorprodukt nur für den dreidimensionalen Raum definiert ist. Das Vektorprodukt ist ein so genannter axialer Vektor, da er bei einer Punktspiegelung unverändert bleibt. Das Vektorprodukt ist antikommutativ, d.h. es gilt:Außerdem ist es distributiv und nicht assoziativ.
Höhere Vektorprodukte
Bildet man das Skalarprodukt zweier Vektoren, so kann man dieses natürlich wieder mit einem weiteren Vektor multiplizieren. Dies geht auf zwei Arten, die oben aufgeführt wurden. Das Spatprodukt ist definiert als das Skalarprodukt aus dem Kreuprodukt zweier Vektoren mit einem dritten:
Skalarmultiplikation
Die Skalarmultiplikation ist die Multiplikation eines Vektors mit einem Skalar, wobei man als Produkt wiederum einen Vektor erhält.
Komponentenweises Produkt
Das komponentenweise Produkt zweier Vektoren wird in manchen Programmiersprachen (z. B. MATLAB) mit „.*“ bezeichnet, z. B.
 .
.
In der Mathematik gibt es keine spezielle Notation dafür, insbesondere spielt das komponentenweise Produkt in der linearen Algebra keine besondere Rolle, da es wesentlich von der gewählten Basis abhängt und es daher keine anschauliche geometrische Interpretation dafür geben kann.
Multiplikationen mit Matrizen
Skalarmultiplikation
Soll eine Matrix mit einer einem Skalar multipliziert werden, so wird jedes Matrixelement mit dem Skalar multipliziert.
 .
.
Matrizenmultiplikation
Zwei Matrizen lassen sich nur multiplizieren, wenn die Spaltenanzahl der ersten Matrix gleich der Zeilenanzahl der zweiten Matrix ist. Dann gilt:
Das Matrizenprodukt ist assoziativ aber nicht kommutativ.
Kartesisches Produkt
In der Mengenlehre bezeichnet man als kartesisches Produkt zweier Mengen A und B die Menge aller geordneten Paare mit erstem Glied aus A und zweitem Glied aus B:
-
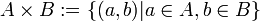 .
.
Der Begriff lässt sich für beliebig viele Mengen verallgemeinern.
Produkt der Kategorientheorie
Hauptartikel: Produkt (Kategorientheorie)
In der Kategorientheorie ist das Produkt einer durch die Menge I indizierten Familie von Objekten
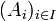 ein Objekt P zusammen mit einer Familie
ein Objekt P zusammen mit einer Familie  von Morphismen
von Morphismen  (genannt Projektionen) mit der folgenden Eigenschaft:
(genannt Projektionen) mit der folgenden Eigenschaft:Für jedes Objekt C und jede Familie von Morphismen
 gibt es genau einen Morphismus
gibt es genau einen Morphismus  mit
mit 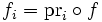 .
.Produkt über einer Indexmenge
Allgemeiner kann das Produkt über einer Indexmenge
 definiert werden:
definiert werden:liest man „Produkt über ak für
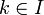 “.
“.Leeres Produkt
Ist die Menge I im Produkt
 gleich der leeren Menge
gleich der leeren Menge  definiert mal den Wert dieses Produkts als 1:
definiert mal den Wert dieses Produkts als 1:Dies wird auch als leeres Produkt bezeichnet.
Also ist zum Beispiel
 weil es keine ganze Zahl gibt, die größer gleich 0 und kleiner gleich als − 1 ist. Dagegen ist
weil es keine ganze Zahl gibt, die größer gleich 0 und kleiner gleich als − 1 ist. Dagegen ist  . So wird auch die Definition von 0!=1 klarer, denn
. So wird auch die Definition von 0!=1 klarer, denn  .
.Literatur
- Bronstein, Semendjajew, Musiol, Mühlig: Taschenbuch der Mathematik. Verlag Harri Deutsch, Frankfurt/Main 20056, ISBN 3-8171-2006-0
- Nolting: Grundkurs Theoretische Physik Bd. 1 - Klassische Mechanik. Springer Verlag, Berlin/Heidelberg 20046, ISBN 3-540-21474-7.
- Arens, Hettlich, Karpfinger, Kockelkorn, Lichtenegger, Stachel: Mathematik. Spektrum Akademischer Verlag, Heidelberg 2008, ISBN 978-3-8274-1758-9.
Wikimedia Foundation.














