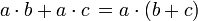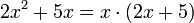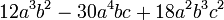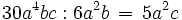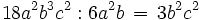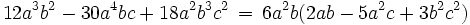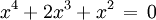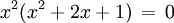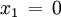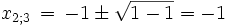Produktzerlegung

In der elementaren Algebra ist es häufig sinnvoll, Summen oder Differenzen in Produkte umzuwandeln. Dies gilt beispielsweise dann, wenn man einen Bruchterm durch Kürzen gemeinsamer Faktoren von Zähler und Nenner vereinfachen will. Eine wichtige Methode in diesem Zusammenhang ist das Ausklammern.

Ausklammern bedeutet, dass man einen gemeinsamen Faktor sucht, der in allen Gliedern der gegebenen Summe oder Differenz enthalten ist, und für diesen Faktor das Distributivgesetz anwendet:

$a \cdot b + a \cdot c \, = a \cdot (b + c)$

Das Ausklammern ist somit die Umkehrung des Ausmultiplizierens. Da eine algebraische Summe in ein Produkt verwandelt wird, spricht man auch von Produktzerlegung oder Faktorenzerlegung.

Das Ausklammern einer gesuchten Größe ist häufig beim Auflösen von Formeln und Gleichungen mit Parametern (Formvariablen) notwendig.

Beispiele

Beispiel 1

2x² + 5x

Der Faktor x ist in beiden Summanden, nämlich in 2x² und in 5x, enthalten und kann daher ausgeklammert werden.

$2 x^2 + 5 x = x \cdot (2 x + 5)$

Die Summanden der Klammer erhält man dadurch, dass man die einzelnen Summanden der gegebenen Summe jeweils durch den ausgeklammerten Faktor (hier x) dividiert. Der erste Summand ergibt sich aus 2x²:x = 2x, der zweite aus 5x:x = 5.

Durch Ausmultiplizieren lässt sich leicht die Richtigkeit der Umformung überprüfen.

Beispiel 2

$12 a^3 b^2 - 30 a^4 b c + 18 a^2 b^3 c^2 \,$

Zunächst gilt es, einen geeigneten gemeinsamen Faktor zum Ausklammern zu finden. Die Zahlen 12, 30 und 18 haben den größten gemeinsamen Teiler 6. Die Variable a tritt in den Potenzen a³, a⁴ und a² auf. Die Potenz mit dem kleinsten Exponenten ist a² und wird daher ebenfalls ausgeklammert. Auch unter den Potenzen von b, nämlich b², b¹ (gleichwertig mit b) und b³, wählt man die Potenz mit dem kleinsten Exponenten aus; statt b¹ schreibt man aber besser vereinfacht b. Die Variable c schließlich kommt nicht in allen Summanden vor; daher klammert man keine Potenz von c aus. Insgesamt wird also 6a²b ausgeklammert.

Wegen

$12 a^3 b^2 : 6 a^2 b \, = \, 2 a b$,

$30 a^4 b c : 6 a^2 b \, = \, 5 a^2 c$

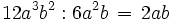und

$18 a^2 b^3 c^2 : 6 a^2 b \, = \, 3 b^2 c^2$

erhält man:

$12 a^3 b^2 - 30 a^4 b c + 18 a^2 b^3 c^2 \, = \, 6 a^2 b (2 a b - 5 a^2 c + 3 b^2 c^2)$

Zur Reduzierung des Grades

Ausklammern kann zur Lösung von Gleichungen höheren Grades verwendet werden. So hat beispielsweise eine Gleichung der Form

$x^k p(x)\,=\,0$,

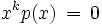wobei p(x) ein Polynom und k eine natürliche Zahl ist, die (mindestens) k-fache Nullstelle x = 0. Die weiteren Lösungen ergeben sich aus p(x) = 0. Damit wurde der Grad der Gleichung um k reduziert.

Beispiel 1

$x^4+2x^3+x^2\,=\,0$

$x^2(x^2+2x+1)\,=\,0$

$x_1\,=\,0$

$x_{2;3}\,=\, -1 \pm \sqrt{1-1}=-1$

(Nach der p-q-Formel)

Aus einer Gleichung 4. Grades (biquadratisch) wurde eine einfach zu lösende quadratische Gleichung.