Pteroides torricellana

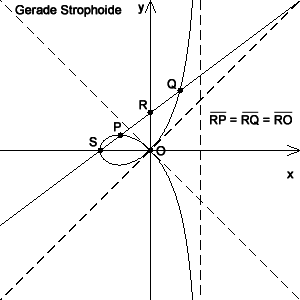
Die Strophoide (adjektivisches Kunstwort von griechisch στροφή, strofí - die Strophe, Wendung, Kurve, Drehung, Biegung), genauer die gerade Strophoide ist eine spezielle ebene Kurve 3. Ordnung.

Gleichungen der geraden Strophoide

• Kartesische Koordinaten: $(a + x) x^2 - (a - x) y^2 \, = \, 0$

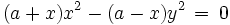
• Polarkoordinaten: $r = - \frac{a \cos(2\varphi)}{\cos\varphi}$

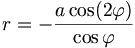
• Parametergleichung: $x = \frac{a (t^2 - 1)}{1 + t^2}; \qquad y = \frac{a t (t^2 - 1)}{1 + t^2}$

Eigenschaften der geraden Strophoide

Im Folgenden wird jeweils vorausgesetzt, dass die Koordinatenachsen so liegen wie in der Skizze.

• Die Punkte der geraden Strophoide sind gekennzeichnet durch die folgende geometrische Eigenschaft: Es seien S der Scheitelpunkt der Kurve und P ein beliebiger Kurvenpunkt, der von S verschieden ist. Bezeichnet man den von S und P verschiedenen Schnittpunkt der Geraden SP mit der Kurve als Q und den Schnittpunkt mit der y-Achse als R, so ist R von P und Q sowie vom Ursprung O gleich weit entfernt.

• Die gerade Strophoide ist achsensymmetrisch bezüglich der x-Achse. Genau zwei Punkte der Kurve liegen auf der Symmetrieachse, nämlich der Ursprung und der Scheitel S mit den Koordinaten ( − a;0).

• Der Ursprung des Koordinatensystems ist ein Doppelpunkt der Kurve, d.h. er wird zweimal durchlaufen. Die beiden Winkelhalbierenden der Quadranten des Koordinatensystems stimmen mit den beiden Tangenten im Ursprung überein.

• Die Gerade mit der Gleichung 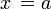$x \,= a$ (in der Skizze gestrichelt) ist Asymptote der Kurve.

• Die Schleife der geraden Strophoide schließt eine Fläche mit dem Inhalt 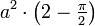$a^2 \cdot \left( 2 - \tfrac{\pi}{2} \right)$ ein.

• Die Fläche, die von der Kurve und der Asymptote begrenzt wird und sich ins Unendliche erstreckt, hat den Flächeninhalt $a^2 \cdot \left(2 + \tfrac{\pi}{2} \right)$.

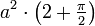• Die Strophoide ist außerdem unter den Namen Ala, Fokale, harmonische Kurve (nach Werth), Kukumaide und Pteroides torricellana bekannt.